Практична РОБОТА №9

Чисельний розв'язок параболічних та еліптичних рівнянь

9.1 МЕТА РОБОТИ

1 Вивчення основних визначень і положень теорії чисельного розв'язку параболічних та еліптичних рівнянь.

2 Вивчення основних методів чисельного розв'язку параболічних та еліптичних рівнянь.

3 Розробка програм і розв'язок на ЕОМ параболічних та еліптичних рівнянь.

9.2 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

Еліптичні рівняння

Як приклади еліптичних рівнянь у часткових похідних можна навести рівняння Лапласа, Пуассона і Гельмгольца.

Якщо ввести оператор Лапласа функції 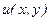, то в загальному вигляді можна записати

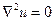- рівняння Лапласа;

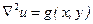- рівняння Пуассона;

- рівняння Гельмгольца.

У рівняннях Лапласа, Пуасона, Гельмгольца одна із мінних може бути як просторовою координатою, так і часом .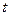

Рівняння Лапласа використовують для математичного опису електромагнітних полів, магнітних полів постійного струму, стаціонарних теплових полів.

Області застосування рівнянь Пуассона – задачі електростатики, електронної оптики, теорії пружності та ін.

Рівняння Гельмгольца є математичною моделлю коливних процесів, наприклад, в акустиці.

Допустимо, що розв’язок еліптичного рівняння належить області Ω з границею Г. Розглянемо найпростіший випадок, коли Ω - прямокутник [ a, b ] x [ c, d ].

Двовимірну область W накриємо сіткою вузлів з координатами (рис 9.1), де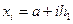

, ; , , ,

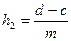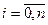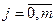- кількість вузлів розбиття; - кроки та сітці.

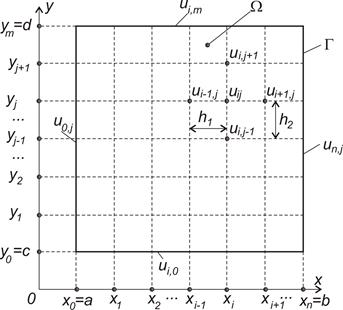
Рисунок 9.1 –Сітка для дискретизації задачі

Вузли називають внутрішніми, коли 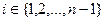, і граничними, коли або та або 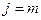, тобто

, ,

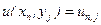, (9.2)

,

, ,

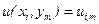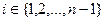Виразимо оператор Лапласа у дискретному вигляді, скориставшись формулою для обчислення наближення до другої похідної

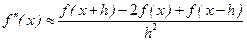. (9.3)

У відповідності з формулою (9.3) будемо мати

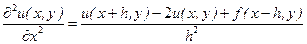, (9.4)

і відповідно

. (9.5)

Якщо - розрахункова точка, то і відповідно

, ,

, ,

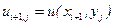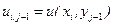де .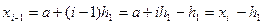

Аналогічно ,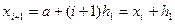

, .

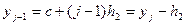Отже, в розрахунковій точці часткові похідні і можна замінити такими різницевими рівняннями:

,

.

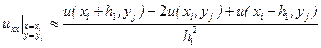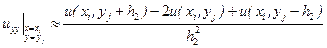Переходячи до прийнятих позначень, отримаємо

, (9.6)

. (9.7)

Таким чином,

. (9.8)

Різницеве рівняння (9.8) можна спростити, якщо крок сітки зробити постійним як за змінною 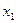, так за змінною тобто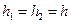

Тоді

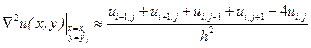. (9.9)

Допустимо, що числовим методом необхідно розв’язати диференціальне рівняння з частковими похідними другого порядку, яке є еліптичним рівнянням

, (9.10)

де 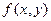- задана функція, а W - прямокутник. Тоді у відповідності з (9.8) запишемо дискретний аналог еліптичного рівняння

.(9.11)

Рівняння (9.10 необхідно доповнити сукупністю граничних умов (9.2) на Г.

Розглянемо техніку обчислення значень функції у вузлах решітки W Розглянемо перших три шари решітки (рис. 9.2). Зафіксуємо значення j. Візьмемо j =1.

Рисунок 9.2 - Перші три шари решітки W

Тоді при із (9.11) отримаємо рівняння

.

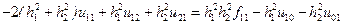Якщо тепер 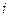змінювати від 2 д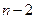о , то

, .

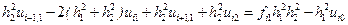І, нарешті, при будемо мати

,

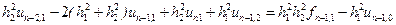де .

Тепер можна взяти j =2 і знову скласти систему із n -1 рівнянь. Повторюючи процес складання рівнянь для , отримаємо систему із рівнянь в якій невідомих.

Параболічні рівняння

Як приклад параболічного рівняння розглянемо рівняння теплопровідності

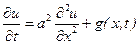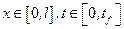, , (9.12)

з початковими умовами за змінною

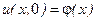при , (9.13)

і крайовими умовами за просторовою координатою х

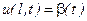, , при . (9.14)

Рівняння (9.12) можна інтерпретувати як задачу визначення температури 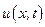тонкого однорідного стержня (бруса) довжиною l, якщо відомий розподіл температури в стержні у початковий момент часу t= 0(початкова умова (9.13))і відома зміна температури на кінцях стержня х= 0 і х=l у будь-який момент часу t (граничні умови (9.14)) Коефіцієнт а² в (9.12) визначається теплофізичними властивостями матеріалу, а функція g(t,x) виражає дію зовнішнього теплового джерела на стержень і вважається заданою.

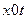Із умов (9.13) і (9.14) видно, що область W - прямокутник зі сторонами у системі координат , а її границя утворена відрізками прямих , , 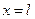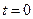і .

Як і раніше розіб’ємо прямокутник на прямокутників зі сторонами і , тобто

, (9.15)

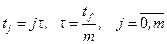. (9.16)

Значення функції у вузлах 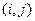позначимо через (рис 9.3) Аналогічне позначення введемо і для функції .

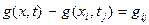Рисунок 9.3 – Сітка області W

Часткові похідн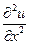і і замінимо різницевими апроксимаціями першого порядку

,

.

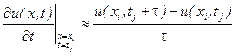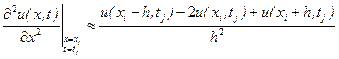Оскільки (див. рис. 9.3) 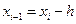, , 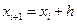то

, (9.17)

(9.18)

Замінюючи в рівнянні (9.12) часткові похідн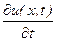і і 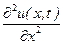їх апроксимаціями (9.14) і (9.15), отримаємо наступне рівняння

, ,

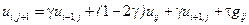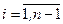, (9.19)

де .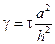

До рівнянь (9.19) слід добавити початкові та граничні умови, які отримаємо шляхом апроксимації функції умов (9.13) і (9.14). Маємо

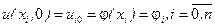, (9.20)

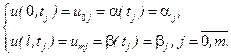(9.21)

Якщо індекси i та j в (9.19) будуть набувати значень від 1 до n -1 і від 1 до m -1 відповідно, то в результаті отримаємо систему (n -2)(m -2) алгебраїчних лінійних рівнянь з (n -2)(m -2) невідомими. Складання такої системи рівнянь опирається на шаблон різницевої схеми (9.16) (рис 9.4).

Рисунок 9.4 - Шаблон різницевої схеми (9.19)

Апроксимація рівняння (9.12) різницевою схемою (9.19) може привести до того, що обчислювальний процес стає нестійкий. Це означає, що помилки, які виникають на одному шарі можуть збільшуватись на наступних парах для деякою . Для того щоб отримати стійку схему обчислень розмір кроку 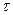повинен підкорятись нерівності .

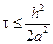Інший спосіб отримання різницевої схеми, яка апроксимує параболічне рівняння (9.12) полягає в апроксимації першої похідної лівою різницею

. (9.22)

Після заміни другої і першої похідних в (9.12) їх апроксимаціями (9.18) і (9.22) отримаємо

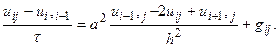
Звідси знаходимо, що

. (9.23)

Зміні, які входять у різницеву схему (9.23), утворюють шаблон, який показаний на рис. 9.5.

Рисунок 9.5 – Шаблон для різницевої схеми (9.23)

Структура системи рівнянь (9.23) така, що значення невідомих можна обчислювати для кожного шару окремо. Враховуючи, що на нульовому шарі значення 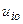відомі, формула (9.23) дає можливість безпосередньо обчислювати всі значення 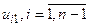для першого шару.

Знаючи значення 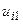першого шару, можна обчислити значення 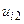для другого шару і т.д.

Отже, для знаходження значень у вузлах першого шару необхідно розв’язати систему лінійних алгебраїчних рівнянь

,

де , , .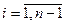

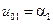Значення величин 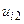у вузлових точках другого шару отримаємо як розв’язок системи

,

де 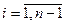, , 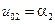, і т. д.

Для передостаннього шару, коли , будемо мати

.

У кожній із двох розглянутих різницевих схем (9.19) і (9.23) для обчислення значень 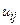на і -ому шарі використовуються значення функції 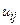, на двох сусідніх шарах. Звідси і їх назва – двошарові схеми.

При цьому різницева схема (9.19), яка є формулою для безпосереднього обчислення шуканих значень 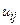носить назву – явної схеми, а схема (9.23), яка для своєї реалізації вимагає розв’язку систем алгебраїчних рівнянь (при переході від шару до шару) називається неявною схемою.

9.3 ЗАВДАННЯ

1 Знайти стаціонарний розподіл температури в квадратній пластині зі стороною 1, який описується рівнянням Лапласа з краєвими умовами виду

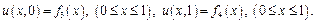
Для розв’язку задачі побудувати сітку із 11 вузлів по та по 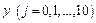. Варіанти завдань у таблиці V.

2 Знайти рішення 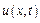для рівняння теплопровідності з постійними коефіцієнтами 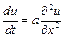, з початковими умовами 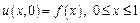і граничними умовами 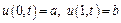. Для розв’язку задачі побудувати сітку із 11 вузлів по та провести розрахунок для 12 шарів по . Розрахунки виконати з кроком 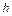по рівним 0.1 і кроком по рівним 0.005. Варіанти завдань у таблиці VІ.

3 Написати програму і розрахувати на ЕОМ розв’язок рівняння.

4 Розробити програму для розв’язку даного рівняння. Розрахувати на ЕОМ значення. Порівняти результати двох методів.

9.4 КОНТРОЛЬНІ ПИТАННЯ

1 До якого класу рівнянь слід віднести рівняння Лапласа?

2 Назвіть області застосування рівнянь Пуассона.

3 Яким чином отримати сітку для дискретизації еліптичного рівняння?

4 Виразіть оператор Лапласа у дискретному вигляді.

5 Отримайте дискретний аналог еліптичного рівняння.

6 До якого класу рівнянь з частковими похідними відноситься рівняння теплопровідності?

7 Отримайте дискретний аналог параболічного рівняння.

9.5 ТАБЛИЦЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ

Варіант	f 1(y)	f 2(y)

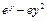
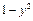
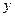
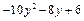
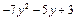
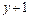
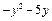
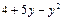
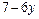
Варіант	f 3(x)	f 4(x)

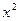
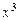
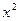
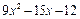
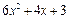
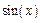
9.6 ТАБЛИЦЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ

Варіант	f(x)	a	b
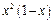
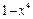
			-0.3
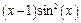
			0.5
		0.5
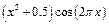
		0.5	1.5
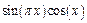
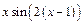
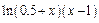
		0.7
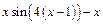
			-1
			-0.4

Дата добавления: 2015-05-23