Практична РОБОТА №8

Чисельний розв'язок гіперболічних рівнянь

8.1 МЕТА РОБОТИ

1 Вивчення основних визначень і положень теорії чисельного розв'язку гіперболічних рівнянь.

2 Вивчення основних методів чисельного розв'язку гіперболічних рівнянь.

3 Розробка програм і розв'язок на ЕОМ гіперболічних рівнянь.

8.2 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

Як приклад гіперболічного рівняння розглянемо математичну модель вільних коливань струни

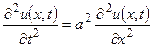, (8.1)

кінці якої зафіксовані у точках х = 0 і х = l. У початковий момент часу кожній точці струни придали початкове зміщення 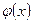і швидкість . Постійна 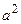у рівняння (8.1) визначається вагою і натягом струни.

Отже, процес коливань струни визначається такими початковими

при , (8.2)

, при , (8.3)

і граничними

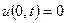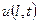, =0 при (8.4)

умовами.

Задача (8.2) – (8.3) визначена на прямокутній області .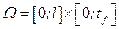

Часткові похідні другого порядку будемо апроксимувати за формулами:

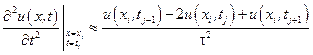, (8.5)

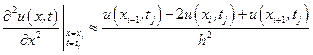. (8.6)

Замінивши у (8.1) часткові похідні і їх наближеннями (8.5) і (8.6), отримаємо різницеву схему

,

яка апроксимує хвильове рівняння (8.1) на шаблоні типу «хрест» (рис.8.1).

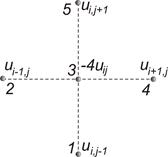
Рисунок 8.1 - Шаблон типу “хрест”

Якщо ввести позначення , то

, (8.7)

де , .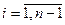

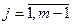Відповідним чином видозмінюється початкова (8.2)

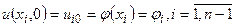, (8.8)

і гранична (8.4)

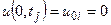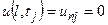, , , (8.9)

умови.

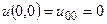Оскільки кінці струни зафіксовані у точках і , то і .

Початкова умова (8.3) задана у диференціальній формі, що вимагає, застосування до неї форм апроксимації. Найпростіша із них

.

Тоді у відповідності з (8.3) 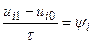або

. (8.10)

У тому випадку, коли функція 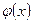має другу похідну, можна скористатися формулою Тейлора порядку два, щоб обчислити значення для другого ряду.

Оскільки . У відповідності з рівнянням (8.1) .

Отже,

. (8.11)

Розкладемо функцію у ряд Тейлора другого порядку. Маємо

,

де ; ;

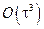- залишковий член ряду Тейлора.

Оскільки, у відповідності з формулою (8.3) а згідно (8.10) то

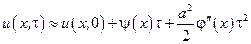. (8.12)

Формулу (8.12) можна застосувати для обчислення значень для першого ряду. Для цього візьмемо , , 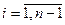а функції 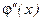апроксимуємо за формулою

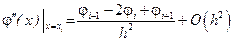, (8.13)

де .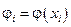

Формули (8.12) і (8.13) дають можливість записати наступну формулу для дискретних значень :

.

Оскільки 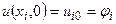, то

.

Якщо врахувати, що , то

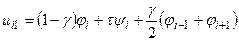. (8.14)

На відміну від формули (8.7), яка забезпечує перший порядок точності 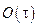, формула (8.10) має другий порядок точності .

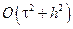8.3 ЗАВДАННЯ

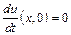1 Розв’язати задачу про коливання струни одиничної довжини із закріпленими кінцями , з початковими умовами , і нульовими граничними умовами .

2 Написати програму і розрахувати на ЕОМ значення кореня зазначеного рівняння.

3 Розробити програму для розв’язку даного рівняння. Розрахувати на ЕОМ значення кореня. Порівняти результати двох методів.

8.4 КОНТРОЛЬНІ ПИТАННЯ

1 Дайте класифікацію систем з розподіленими параметрами.

2 Сформуйте граничні і початкові умови для гіперболічного рівняння.

3 Отримайте дискретний аналог гіперболічного рівняння.

8.5 ТАБЛИЦЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ

Варіант	f(x)	a	b	c
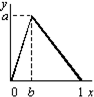
			0.1	-
		0.1	-
		0.2	-
		0.3	-
		0.4	-
		-	-	-
		-	-	-
		-	-	-
		-	-	-
		-	-	-
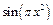
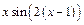
			0.1	0.2
		0.2	0.4
		0.4	0.6
		0.6	0.8
		0.8	0.9

Дата добавления: 2015-05-23