Практична РОБОТА №6

Чисельний розв'язок диференціальних рівнянь методами Ейлера, Гюна і Рунне-Кутта

6.1 МЕТА РОБОТИ

1 Вивчення основних визначень і положень теорії чисельного розв'язку диференціальних рівнянь.

2 Вивчення основних методів чисельного розв'язку диференціальних рівнянь.

3 Розробка програм і розв'язок на ЕОМ диференціальних рівнянь.

6.2 КОРОТКІ ТЕОРЕТИЧНІ ВІДОМОСТІ

1 Основні визначення

Процес проектування автоматичних систем керування передбачає створення математичних моделей технологічних об’єктів. Такі моделі у більшості випадків мають вигляд диференціальних рівнянь. Для отримання відомостей про властивості об’єктів необхідно знати розв’язки їх моделей. Отримати аналітичний розв’язок таких моделей можна тільки в окремих випадках. У переважній більшості для розв’язку диференціальних рівнянь застосовують числові методи.

Методи розв’язку диференціальних рівнянь

Метод Ейлера. Він має обмежене застосування із-за великої похибки, яка накопичується у процесі обчислень.

Отже, будемо розглядати звичайне диференціальне рівняння першого порядку

, (6.1)

з початковою умовою

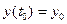, (6.2)

де 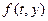- деяка відома у загальному випадку нелінійна функція двох аргументів.

Будемо вважати, що для даної задачі (6.1), (6.2), яка носить назву задачі Коші виконуються вимоги, які забезпечують існування і єдність на відрізку 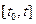її розв’язку .

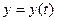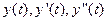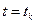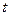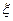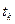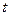Допустимо, що неперервні. Використовуючи теорему Тейлора, розкладемо функцію у ряд Тейлора в околі точки . Для кожного значення існує таке , яке лежить між і , що

.

У відповідності з (6.1) .

Тому .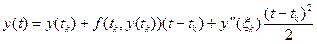

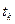Нехай і , а - точка, яка лежить між і 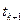. Тоді

.

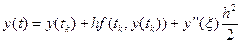Якщо довжина кроку h вибрана досить малою, то членом другого порядку можна знехтувати і отримати

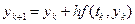, (6.3)

де .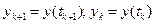

Ітераційна процедура (6.3) і є наближенням Ейлера для задачі (6.1), (6.2) при цьому .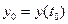

Як випливає із формули (6.3) кожна наступна ордината, починаючи із 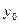, обчислюється шляхом додавання до неї площі прямокутника 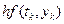(рис 6.1).

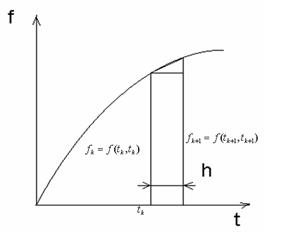
Рисунок 6.1- Ілюстрація процесу утворення

прямокутників в ітераційній процедурі (6.3)

Метод Гюна. Проінтегруємо ліву і праву частини рівняння (6.1) в межах від t₀ до t₁:

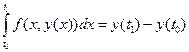. (6.4)

Із рівняння (6.4) знайдемо:

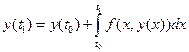. (6.5)

Інтеграл, який знаходиться у правій частині рівняння (6.5), можна наближено обчислити за формулою трапецій:

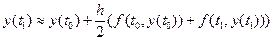. (6.6)

Права частина рівняння (6.6) вимагає знання 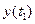, яке знайдемо, скориставшись методом Ейлера. Із формули (6.3) для k=0 отримаємо:

.

З врахуванням значення 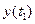формула (6.6) набуде такого вигляду:

.

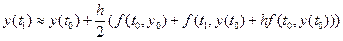Тепер, зробивши заміну 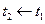, , 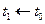генеруємо процес, який наближує праву відповідному розв’язку Задачі Коші .

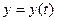Для k -го кроку обчислень будемо мати:

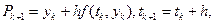(6.7)

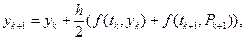(6.8)

де k=0,1,2…

Залишковий член у формулі трапецій, який використовують для наближення інтервалу в (6.6), дорівнює:

. (6.9)

Метод Рунне-Кутта. Ідея побудови методів Рунге-Кутта p - го порядку полягає в отриманні наближеного числового розв’язку задачі Коші за формулою:

, (6.10)

де 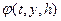- деяка функція, яка наближує відрізок ряду Тейлора до p -го порядку і не вміщує часткових похідних функції .

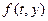Якщо в (6.10) замінити 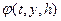на 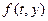, то отримаємо метод Ейлера, тобто метод Ейлера можна вважати частковим випадком методів Рунге-Кутта, коли p=1.

Для побудови методів Рунне-Кутта вище першого порядку функцію 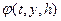вибирають як таку, що залежить від певних параметрів, які вибирають шляхом порівняння виразу (6.10) з многочленом Тейлора для з бажаним порядком степеня.

Розглянемо випадок p=2 і візьмемо функцію 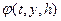з наступною структурою:

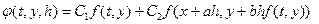. (6.11)

Розкладемо функцію двох змінних 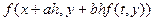в ряд Тейлора, обмежившись лінійними членами:

.

Її підстановка в (6.11) дає:

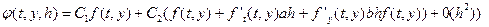
де , .

Підставивши останній вираз в (6.10), отримаємо:

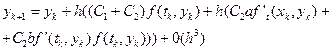. (6.12)

Розкладемо тепер функцію 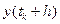в ряд Тейлора, враховуючи члени першого і другого порядків:

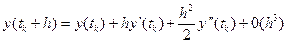. (6.13)

Оскільки 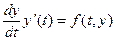, то .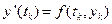

Знайдемо другу похідну 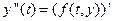. За формулою повної похідної будемо мати:

.

Враховуючи значення 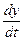, отримаємо:

.

Отже:

.

Тепер значення 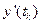і 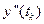можемо підставити у вираз (6.13). У результаті отримаємо:

. (6.14)

Порівнюючи між собою вирази (6.12) і (6.14) приходимо до висновку, що:

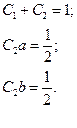
Отримана система із трьох рівнянь, яка вміщує чотири невідомих. Це означає, що один із параметрів вільний і його можна вибрати довільним. Візьмемо , де 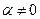. Тоді:

, .

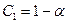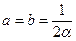У результаті підстановки значень C₁, C_{2 ,} a і b у формулу (6.11) маємо:

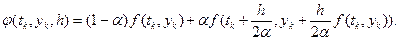
Отриманий результат дає підставу ітераційну процедуру (6.10) записати у такому вигляді:

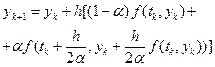. (6.15)

Якщо в (6.15) , то:

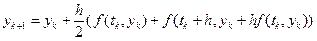, (6.16)

а при 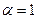маємо:

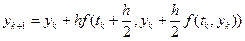. (6.17)

Ітераційна процедура (6.16) носить назву метода Хойна, а (6.17) – породжує метод середньої точки.

Аналіз методів Рунге-Кутта другого порядку дає уявлення в якій формі слід шукати метод Рунге-Кутта довільного порядку.

За аналогією (6.11) можемо записати:

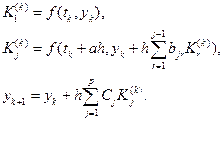(6.18)

Найпоширенішим із сімейства методів (6.18) є метод четвертого порядку (p=4) або просто метод Рунге-Кутта, який породжує таку ітераційну процедуру:

(6.19)

Метод Рунге-Кутта дає похибку накопичення четвертого порядку – 0(h⁴).

Бажання підвищити точність методу Рунге-Кутта привело до появи різних його версій. Одна із них метод Кутта-Мерсона з вибором кроку на кожній із ітерацій.

На k - ому кроці розв’язку задачі Коші послідовно обчислюють:

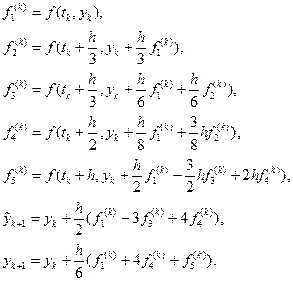6.20)

Після цього підраховують величину

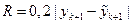, (6.21)

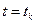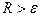і, якщо , то вважають, що в точці отриманий розв’язок задачі Коші з точністю . У тому випадку, коли крок h зменшують вдвічі і знову обчислюють значення 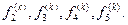При переході до наступного кроку k+1 здійснюється перевірка на можливість збільшення кроку. Якщ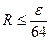о , то .

6.3 ЗАВДАННЯ

1 Чисельно розв’язати дифрівняння з таблиці.

2 Записати всі співвідношення, що необхідні для розробки алгоритму програми.

3 Написати програму і розрахувати на ЕОМ значення кореня зазначеного рівняння.

4 Розробити програму для розв’язку даного рівняння. Розрахувати на ЕОМ значення кореня. Порівняти результати двох методів.

6.4 КОНТРОЛЬНІ ПИТАННЯ

1 Що називається коренем рівняння?

2 Визначення простого і кратного кореня.

3 Основні етапи пошуку кореня.

4 Визначення швидкості і порядку збіжності чисельного методу пошуку кореня.

5 Визначення інтервалу невизначеності кореня.

6 Метод Ейлера.

7 Метод Гюна.

8 Метод Рунге-Кутта.

6.5 ТАБЛИЦЯ ІНДИВІДУАЛЬНИХ ЗАВДАНЬ

№	f(x,y)	y0
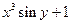
		0.0
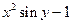
		0.1
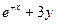
		2.0
		0.3
		0.4
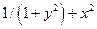
		0.0
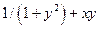
		0.1
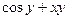
		0.2
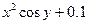
		0.3
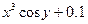
		0.4
		0.5
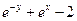
		0.0
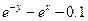
		0.5
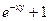
		0.4
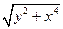
		0.3

Дата добавления: 2015-05-23