Індивідуальні та Колективні моделі позовів

Регулярним є потік подій, які наступають послідовно через чітко визначені проміжки часу. Потік без після дії – це потік настання події якого не залежить від подій в інші проміжки часу.

Ординарний потік – події за незначний проміжок часу або не настають або настають лише по 1.

Стаціонарний потік – настання певного числа подій за певний проміжок часу залежить лише від довжини і не залежить де на осі часу він розміщений.

Найпростіший потік – це потік без після дії ординарності та стаціонарності.

Загалом процес запитів - це довільний точковий (дискретний) процес, тобто довільна випадкова послідовність точок. Найчастіше при цьому використовується пуассонівська модель запитів

1. Число подій які настали за проміжок часу [0:t] розраховується по такій формулі

2. Математичне сподівання ;

3. Імовірність того що за проміжок часу [0:t] настане менше К подій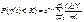

4. Імовірність того що за проміжок часу [0:t] не настане жодної подій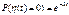

5. Імовірність того що за проміжок часу [0:t] настане не менше К подій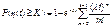

6. Імовірність того що за проміжок часу [0:t] настане хоча б 1 подія

Знайти імовірність того що інтервал часу між двома сусідніми запитами менший за 2 дні;

; t = 2 дні або 2/7 тижня

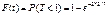
3. Суть та методи визначення ризикової надбавки.

Сума виплати страхового відшкодування і страхова сума не завжди співпадає. З метою покриття дефіциту резервного страхового фонду при настанні страхових випадків частіше ніж середнє значення доцільно розраховувати ризикову надбавку.

Випадок А: розрахунок відбувається за таблицею Муавра-Лапласа

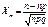Де m – кількість запитів,n – кількість респондентів,р – імовірність настання події,q – імовірність ненастання події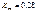

Випадок Б: Розрахунок проводиться по інтегральній формулі Муавра-Лапласа

Якщо необхідно знайти мінімальне число договорів які треба укласти щоб з надійністю 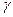можна очікувати що частки страхових подій відхилення від імовірності страхових подій Р на число 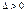, використовується нерівність

Величина можливого перевищення середнього числа настання страхових випадків

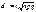
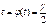
Дата добавления: 2015-05-23