Природа местных сопротивлений

Коэффициент гидравлического трения. Опыты Никурадзе. Зоны сопротивления.

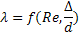
- относительная шероховатость.

Никурадзе провел большое количество опытов в которых варьировали Q, 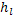, t-вычислялось

Re, -изменялось.

Зоны:

1- Зона ламинарного режима.

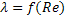
Место для формулы.

2- Область нестационарного режима. Развитие турбулентности.

3- Зона гидравлически гладких труб.

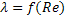
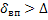
4- Область доквадратичного сопротивления. (или область перехода от гидравлически гладких к шероховатым трубам)

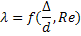
5- Область квадратичного сопротивления..

Практические способы определения

Основной областью турбулентного потока является квадратичная область.

В реальных трубопроводных системах возникает и доквадратичной области.

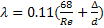^0.25

Метод Шевелёва

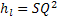
Для квадратичной области, формула Альтштуля и Шифринсона, где

^0.25

Физическая природа местных сопротивлений.

Физическую природу разберём на примере обтекания перегородки.

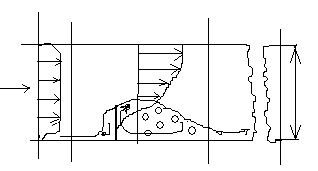
1-2 водоворотный участок на котором в потоке выделяются 2 области:

1) Транзитный поток

2) Водовороты.

Линия авd разделяет эти 2 области. Здесь транзитный поток граничит с медленно движущейся жидкости в водовороте.

Взаимодействие водоворота и транзитного потока приводит к появлению больших поперечных пульсаций скорости.

В результате возникают огромные касательные напряжения пропорциональные произведению пульсаций.

Огромные силы турбулентного трения тормозящие поток, значит местные сопротивления приводят к изменению величины и направлению скорости и появлению больших сил турбул.трения внутри потока.

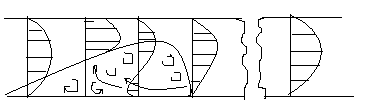
При обтекании преграды в водоворотной области происходит искревление линий тока и сжатие потока. Сжатие достигает максимума за преградой затем поток расширяясь, образует большую водоворотноу область, заполненную вихревыми образованиями с вертикальной осью вращения.

Поперечное чередование вихрей приводит к тому, что линия а,в,с,d и длина большого водоворота пульсирует, пульсирует и длина водоворота длина составляет 20% величин.

Пульсация линии раздела b,c,d вызывает появление больших поперечных пульсаций и вместе с ними на линии b,c,d возникают большие турбулентные касательные напряжения пропорциональные 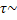V^|U^| и по линии раздела водоворотной области и транзитного потока действуют огромные силы турбулентного трения вызывающие потери напора.

Все это сопровождается деформации эпюр скорости, изменением скорости по величине и направлению. Режим в этой зоне не стационарный.

Участок 1-2 нельзя описать уравнением Бернулли, т.к движение нестационарное.

Участок 2-3- участок восстановления длина= (20-50)d, или (20-50)h.

При отходе от сечения

2-2- движение очень быстро становится плавно изменяющимся, пульсации уменьшаются, эпюра скорости восстанавливается и за сечением 2-3 движение становится равномерным.

Длина влияния местного сопротивления невелика, и поэтому потери по длине здесь очень малы и ими пренебрегают.

H_w=h_l+h_M

Сложность явления объясняет причину по которой большинство местных сопротивлений изучены лишь экспериментально, и только некоторые сопротивления имеют теоретическую формулу.

Дата добавления: 2015-05-23