Побудова цифрових схем

ВСТУП

Контрольні запитання

1. Що називається моментом інерції тіла?

2. Вивести формулу для моменту інерції однорідного диску.

4. Вивести формулу для періоду коливань крутильного маятника.

7. У чому полягає методика визначення моменту інерції тіла неправильної ґеометричної форми з застосуванням крутильного маятника?

8. Вивести формулу для визначення моменту інерції тіла неправильної ґеометричної форми.

Рекомендована література

1. Курс фізики / За редакцією І.Є.Лопатинського.

– Львів: Вид. «Бескид Біт», 2002.

2. Трофимова Т.И. Курс физики.– М.: Высшая школа, 1990.

3. Савельев И. В. Курс общей физики, т.1 –М.: Наука, 1982.

Після виготовлення першого комп'ютера стало ясно, що при його виробництві можливе використання тільки цифрових технологій - обмеження сигналів зв'язку одиницею і нулем додало більшої надійності та простоти архітектури персонального комп’ютера. Завдяки своїй бінарній природі, математична логіка отримала широке поширення в інформатиці. Були створені електронні еквіваленти логічних функцій, що дозволяло застосовувати методи спрощення булевих виразів, що призводило до спрощення електричної схеми. Крім того, завдяки можливості знаходження вихідної функції по таблиці скорочувався час на пошук необхідної логічної схеми.

У даній курсовій роботі буде даний один із логічних виразів, який буде розв’язуватися, як і в ручну так і за допомогою пакетів прикладних програм (ППП). А саме ППП Proteus, ППП ORCAD та ППП Electronics WorkBench (EWB). Всі пакети надзвичайно сильні у розрахунку цифрових схем. Завдяки даним програмам можна відтворювати процеси, якщо практично – це важко або неможливо зробити. Наприклад певна людина склала електричне коло і хоче дізнатися характеристики кола, при його підключені до джерела. А відповідних вимірювальних пристрої нема, то можна цю ж схему промоделювати у ППП EWB. Даний пакет місти повен набір елементів, завдяки яких можна класти будь-яке електричне коло.

Дана курсова робота дає можливість ближче познайомитися з речами, які необхідні сучасній людині.

1 АНАЛІЗ ЗАВДАННЯ ТА ВИБІР МЕТОДУ СИНТЕЗУ

Для відображення процесів, які відбуваються в ЕОМ, використовують математичний апарат алгебри логіки, або бульової алгебри (за іменем її творця англійського математика Джорджа Буля). Ця алгебра оперує змінними, які можуть набувати тільки одне з двох різних значень – «хибність» та «істина», що відповідає значенням «0» і «1» двійкових змінних. Основою алгебри логіки є поняття логічної функції виду f(X1, X2,…,Xn), відносно аргументів
X1, X2, …, Xn, яка, як і її аргумент може приймати тільки два значення – 0 і 1. Логічна функція може бути задана словесно, алгебраїчним виразом, діаграмою або таблицею істинності. Іноді логічні функції розглядаються як логічні операції над двійковими величинами, тому що вказують на правило перетворення одних двійкових величин в інші [1].

В даній курсовій роботі розглядається один з процесів, який реалізується в ЕОМ, і він задається функцією наступного вигляду:

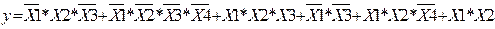. (1.1)

Головне завдання мінімізувати даний процес (логічну функцію) у більш просту, привести її до мінімальної форми, але так щоб кінцеве значення виразу не змінилося. Це дасть можливість реалізувати функцію використавши мінімум апаратних витрат.

Найпростішими методами мінімізації функцій відносно невеликої кількості змінних є діаграми Вейча, карти Карно, метод Квайна-Мак-Класкі і аналітичні перетворення функцій з використанням аксіом і законів алгебри логіки.

Діаграми Вейча зручно застосовувати для мінімізації логічних функцій що містять не більше, як 4 – 6 змінних. Ці діаграми являють собою спеціально організовані таблиці істинності. Кількість клітинок у таблиці відповідає кількості можливих наборів аргументів – 2ⁿ. Клітинки нумерують для простішого заповнення її аргументами а потім і для перевірки знайдених значень.

Мінімізація полягає в охопленні клітинок з одиничним значенням функцій на діаграмі Вейча спеціальними контурами, які охоплюють 1, 2, 4, 8 і т.д. сусідніх клітинок у вигляді прямокутника чи квадрата.

Значення функції записується таким чином, що для кожного контуру в МДНФ включають кон’юнкцію змінних або їх інверсій, які не змінюють свого значення для всіх клітинок, охоплених контуром [1].

Ще один метод, яким спробуємо мінімізувати дану функцію, буде мінімізація на основі законів та аксіом алгебри логіки. Даний метод теж не виявляє до себе використання багатьох зусиль при розв’язанні даної або іншої логічної функції. Для спрощення функції даним методом потрібно використовувати закони та аксіоми алгебри логіки, які розглянемо далі [1].

Аксіоми алгебри логіки:

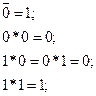(1.2)

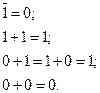(1.3)

Дані аксіоми будемо використовувати тоді, коли будемо заповняти таблицю істинності.

Нижче приведемо закони алгебри логіки, які використовуються при перетвореннях логічних функцій та їх мінімізації.

Комутативний закон використовуватимемо при сортуванні доданків логічної функції:

х1*х2= х2^*х1; (1.4)

х1+х2=х2+х1. (1.5)

Для представлення логічного виразу, групуючи доданки у дужках, використовуємо асоціативний закон:

х1*(х2*х3)=(х1*х2) *х3= х1*х2 *х3. (1.6)

Ще одним із законів, які будемо використовувати при приведені функції до базису, буде закон подвійної інверсії:

(1.7)

Закон універсальної множини, будемо використовувати при скорочені дужок у логічному виразі:

(1.8)

(1.9)

Дистрибутивний закон, потрібен при винесені спільного множника за дужки:

х1*(х2+х3)= х1*х2+ х1*х3; (1.10)

х1+(х2*х3)= (х1+х2)*(х1+х3). (1.11)

Більшість законів і аксіом будуть використані при спрощені заданої функції.

В даній курсовій роботі буде проведена мінімізація логічної функції обома методами. Якщо говорити про переваги та недоліки, то можна сказати, що обидва методи дають нам мінімізовану, просту функцію, а це зменшить витрати на реалізацію даної задачі. «Мінус» – за мінімізуючи функцію за законами алгебри логіки і за діаграмою Вейча можна отримати два різних розв’язки, обидва з яких будуть правильними. Це приводить спочатку до непорозуміння, але при перевірці за таблицею істинності, по одному з тактів, ми побачимо, що мінімізована функція в одному і в другому випадку є правильна, і дає один і той же розв’язок.

Буде проведена перевірка значення не мінімізованої логічної функції та мінімізованої за допомогою таблиці істинності.

Буде приведено мінімізовану функцію до двох базисів І-НІ та АБО-НІ. При цьому будемо використовувати закони інверсії (правила де Моргана):

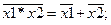(1.12)

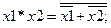(1.13)

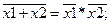(1.14)

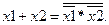(1.15)

Буде проведена побудова часових діаграм за цими базисами.

Наступним етапом курсової роботи буде перевірка попередніх розрахунків. А саме, знову буде приведено функцію до базисів АБО-НІ та І-НІ тільки не вручну, а за допомогою Proteus. У EWB буде змодельована задана логічна функція (1.1). В ППП OrCAD буде змодельована мінімізована логічна функція, яку буде отримано за допомогою діаграм Вейча. При цьому з а допомогою даних пакетів програм буде здійснена перевірка у попередніх розрахунках.

В завданні КР, поставлене завдання привести функцію до досконало диз’юнктивної нормальної форми (ДДНФ) та досконало кон’юнктивної нормальної форми (ДКНФ), ця задача буде розказана в одному з наступних розділів. Також у цей розділ увійде реалізація логічної функції за допомогою мультиплексора, як це розглядається в [2]. І останнім робочим розділом буде розробка програми на мові Visual Basic for Application (VBA), яка буде розраховувати значення «істинності» чи «не істинності» мінімізованої логічної функції на будь – якому такті.

2 МІНІМІЗАЦІЯ ЛОГІЧНИХ ФУНКЦІЙ

Проектування елементів і схем, як правило, супроводжується мінімізацією логічних функцій, тобто приведення їх до мінімальних форм. Це викликано тим, що реалізація функцій, поданих в мінімальній формі, забезпечує, в свою чергу, мінімум апаратних витрат на їх реалізацію.

В даному розділі спробуємо мінімізувати задану логічну функцію
(1.1) двома методами: за допомогою діаграм Вейча і за законами та аксіомами алгебри логіки, які досліджувалися в попередньому розділі [3].

2.1 Мінімізація логічної функції за допомогою законів та аксіом алгебри логіки

За номером варіанта задано логічну функцію вигляду:

.

Проведемо мінімізацію. Знайдемо спільні аргументи Х_і, де і= які є в кожному з добутків, або в декількох, і виносимо їх за дужки:

.

За законом універсальних множин та за доповняльним законом, вираз, який знаходиться в дужках скоротиться до одиниці, а, значить, функція набуває вигляду:

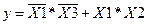. (2.1)

2.2 Мінімізація логічної функції за допомогою діаграмою Вейча

Задана таж сама логічна функція (1.1).

За методом діаграм Вейча потрібно побудувати табличну форму розмірністю 2ⁿ, де n – кількість іксів. В даному випадку маємо чотири значення Х, тобто таблиця має бути розмірністю у шістнадцять комірок [1]. Дана діаграма зображена на рисунку 2.1.

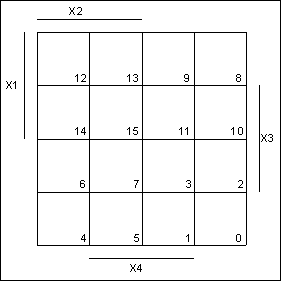
Рисунок 2.1 – Діаграма Вейча для
чотирьох змінних

Далі аналізуємо функцію (1.1) і розпочинаємо заповняти діаграму.

Діаграма заповнюється за наступним алгоритмом:

1. Розглядають кожен з доданків логічної функції.

2. Беремо довільний доданок. Усі його аргументи утворюють певні зони на діаграмі Вейча.

3. Визначають діапазони дії кожного з аргументів.

4. Вибираються комірки, які лежать на перетині зон усіх аргументів доданку і в них записуємо «одиниці».

5. Повторюємо все з другого пункту з іншими доданками рівняння.

Розглядаємо перший доданок . Зона значень
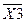є [0,1,2,3,4,5,6,7], є [4,5,6,7,12,13,14,15], є [0,1,4,5,8,9,12,13]. Спільними для цих аргументів є комірки під номером 4 та 5, записуємо в них «одиниці».

Беремо наступний доданок 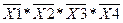. Визначаємо діапазони. Зона значень є [0,1,2,3,4,5,6,7], 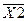є [0,1,2,3,8,9,10,11], 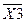є [0,1,4,5,8,9,12,13],
є [0,2,4,6,8,10,12,14]. Спільними комірками для цих аргументів є комірка під номером 0, куди й записуємо «одиничку».

Аналогічно визначимо зону на діаграмі Вейча для наступного доданку . Діапазони 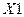є [8,9,10,11,12,13,14,15], є [4,5,6,7,12,13,14,15], 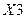є [2,3,6,7,10,11,14,15]. Спільні комірки для даних аргументів є 14 та 15, записуємо в них «одинички».

Розглядаємо доданок 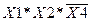. Діапазони для цих аргументів виписуємо з попередніх спостережень 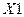є [8,9,10,11,12,13,14,15], є [4,5,6,7,12,13,14,15],
є [0,2,4,6,8,10,12,14]. Спільні комірки 12 та 14, записуємо «одинички» в ці комірки.

Розглядаємо доданок аргументів 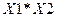. Діапазон для даних іксів буде
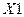є [8,9,10,11,12,13,14,15], є [4,5,6,7,12,13,14,15]. Спільні комірки 12, 13, 14, 15, але оскільки в комірки 14 та 15 вже «одиниці» записані то «одинички» записуємо тільки у 12 і 13.

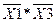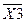Розглядаємо останній доданок . Для цих аргументів діапазон буде є [0,1,2,3,4,5,6,7], є [0,1,4,5,8,9,12,13]. Перша комірка є спільною для даних аргументів, тому в неї записуємо останню «одиницю».

Інші комірки залишаємо порожніми. Комірки, які заповнені «одиницями», об’єднуємо спеціальними контурами у зони. Результат розрахунків і проведення контурів показано на рисунку 2.2.

Рисунок 2.2 – Заповнена діаграма Вейча
з визначеними контурами

Отже, діаграма заповнена, контури визначені, тепер мінімізуємо логічну функцію. Зони на діаграмі показують відповідь, тільки її потрібно знайти у вигляді логічної функції. Для цього переглядаємо кожну зону і знаходимо, які аргументи повністю характеризують усю зону. Знайдені таким чином аргументи перемножуємо, а самі мультиплікативні вирази додаємо. Зона обведена кружечком, вміщає в собі значення 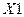та , а зона еліптичного типу вміщає в собі значення функції та 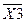. Тепер запишемо мінімізовану функцію:

.

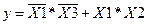Якщо звернутися до пункту 2.1 і перевірити розв’язок за діаграмами Вейча та за законами алгебри логіки, то побачимо, що мінімізована функція в першому і другому методах збігається.

3 ПРЕДСТАВЛЕННЯ ЛОГІЧНИХ ФУНКЦІЙ У БАЗИСІ

У попередньому розділі було виконано мінімізацію логічної функції, для того, щоб схема мала мінімальну форму, що, в свою чергу, забезпечує, мінімум апаратних витрат на її реалізацію та мінімальну затримку часу.

У даному розділі виконаємо приведення логічної функції до базисів І-НІ та АБО-НІ [4]. Це, в свою чергу, також забезпечить зменшення витрат на реалізацію схеми, оскільки на схемі лише один типовий елемент «АБО – НІ» чи «І – НІ». Але недолік цих перетворень в тому, що іноді функція, приведена до базису, має розширену форму, тобто вона більш велика і незручна, ніж мінімізована функція.

3.1 Приведення логічної функції до базису «І-НІ»

Маємо мінімізовану функцію 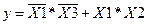, яку потрібно привести до одного базису «І-НІ», тобто потрібно, щоб функція містила лише одну типову операцію в рівнянні, а саме: логічне множення та інверсію.

Функція (2.1) має два множники, які додаються. Нам потрібно замінити логічне додавання на логічне множення з інверсією. Проведемо подвійне інвертування усього виразу. Одну інверсію ставити неможна, оскільки функція змінить своє значення на протилежне. Отже, використовуючи закон подвійної інверсії (1.7), запишемо:

.

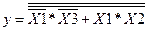За правилом де Моргана (1.14) розбиваємо нижню інверсію даного виразу, при цьому змінюючи знак логічного додавання на знак логічного множення:

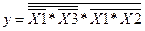. (3.1)

Таким чином, було реалізовано мінімізовану функцію в базисі «І-НІ» і тепер у логічної функції присутня тільки операція кон’юнкції та інверсії.

3.2 Приведення логічної функції до базису «АБО-НІ»

Скористаємось мінімізованою у другому розділі логічною функцією (2.1). У даному підрозділі потрібно перевести її у базис «АБО-НІ», тобто потрібно, щоб логічна функція містила лише операцію логічного додавання з інвертуванням.

За правилом де Моргана (1.14), над першим із доданків (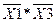) не потрібно ставити подвійну інвертацію, а потім розбивати нижню інверсію, можна відразу записати що, 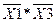= . Скориставшись законом подвійної інверсії (1.7) над другим доданком, потрібно провести подвійну інвертацію і за правилом (1.12), замінити знак логічного множення на логічне додавання 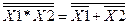. Отже, мінімізована функція 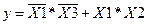у базисі «АБО-НІ» матиме вигляд:

(3.2)

Оскільки функція подається у базисі «АБО-НІ», то над загальним додаванням проведемо подвійну інверсію, значення функції від цього не зміниться (1.7), але при побудові схеми стане можливим використовувати лише один елемент «АБО-НІ» із двома входами.

В даному розділі було виконано поставлене завдання: логічна функція приведена до двох базисів «І-НІ» та «АБО-НІ». Тепер потрібно провести перевірку на предмет того, чи збігатимуться кінцеві сигнали немінімізованої функції, мінімізованої та сигнал цієї ж функції в двох базисах. Це можна зробити за допомогою таблиць істинності. Побудувавши її, порівняємо усі результуючі сигнали. Цю побудову буде наведено у наступному розділі.

4 ПОБУДОВА ТАБЛИЦЬ ІСТИНОСТІ

Як згадувалося у попередньому розділі, ми будуємо таблиці істинності для того, щоб перевірити, чи не змінюється кінцеве значення логічної функції від її мінімізації, різними методами, від приведення мінімізованої функції до будь-якого з базисів.

Тому завдання на даний розділ полягає у перевірці виконаної роботи, а також у підтверджені гіпотези, що незалежно від того, яку функцію подати – мінімізовану чи немінімізовану, її кінцеве значення від цього не зміниться.

4.1 Побудова таблиці істинності не мінімізованої функції і мінімізованої за діаграмами Вейча

Розпочнемо будувати нашу таблицю істинності. Значення аргументів від 0-15 заповняються відповідно за своїми тактами.

В колонку під назвою «мінімізація за діаграмами Вейча» переписуємо дані з діаграми Вейча (див. рис. (2.2)), де кожному такту відповідає певне значення. Але для впевненості запишемо приклад для мінімізованої функції за діарамою Вейча 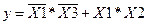для декількох тактів, наприклад, для 1 та 12 тактів.

Для даної перевірки звернемося до аксіом алгебри логіки (1.2), (1.3).

По першому такті: ;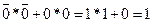

По дванадцятому: .

І для цих же тактів зробимо перевірку за немінімізованою функцією.

Перший такт: Даний вираз містить другий доданок «», який дорівнює «1», тому далі вести розрахунок не потрібно оскільки за законом (1.9), щоб не додавалось до одиниці, завжди буде одиниця.

Дванадцятий такт: 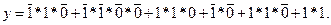Тут також є два доданки, які відразу перетворюють весь вираз в «1». Це - «» та «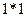». Далі таблиця заповнюється аналогічно. Для кожного такту у функцію підставляємо своє значення аргументу. Цей розрахунок представлений в таблиці А.1.

4.2 Побудова таблиці істинності для не мінімізованої та для мінімізованої за законами та аксіомами алгебри логіки

В побудові немінімізованої функції нічого, з попереднього підрозділу, не змінилося.

А для мінімізованої за законами алгебри логіки функції шукаємо вихідні дані так само, як і для немінімізованої функції. Різниця в тому, що у мінімізованій функції менше значень аргументів .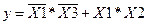

Таблиця істинності заповнена і наведена в таблиці А.2.

Навіть поверховий аналіз даної таблиці підтверджує, що результуючі значення функцій збігаються. Проте проведемо більш ґрунтовне дослідження. Для цього візьмемо довільні такти 4 та 15 і покажемо розрахунок за цими тактами для немінімізованої та мінімізованої функції за законами АЛ. Визначимо результуючі значення функції мінімізованої на основі законів АЛ для такту №4.

.

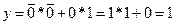Виконаємо аналогічні розрахунки для такту №15:

.

Перевіримо ці результати для не мінімізованої функції. Розрахуємо значення немінімізованої функції для четвертого такту:

.

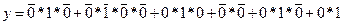Добуток «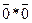» дає «одиницю», тому за аксіомою (1.3), сума добутків перетвориться в «1».

Перевіримо дану функцію за п’ятнадцятим тактом.

.

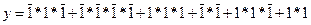Даний вираз також містить добуток, який робить з усього виразу «одиницю» (1*1*1).

Отже, можна сказати, що оскільки результати однакові, то і функція не змінилася від того, що була мінімізована.

4.3 Побудова таблиці істинності для нелінійної функції та для мінімізованої функції в базисах «І-НІ» та «АБО-НІ»

Функція в базисі повинна характеризуватися тими ж значеннями функції на усіх тактах, що і звичайна функція, хоча вона містить одну логічну операцію логічне додавання або множення з інвертуванням. Перевіримо, чи змінилися значення вихідного сигналу після приведення його до будь якого базису [5].

Для функції в базисі «І-НІ» зробимо розрахунок по 10^ому такту і перевіримо його з будь-якою таблицею з попередніх підпунктів 4.1 та 4.2:

; .

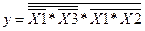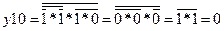Переглянувши таблиці 4.1 та 4.2, бачимо, що значення функції в базисі «І-НІ», мінімізованої та не мінімізованої функцій по десятому такту збігаються.

Тепер для базису «АБО-НІ» виконаємо аналогічну перевірку, тільки для іншого такту, наприклад, для восьмого:

;

Подвійна інверсія скорочується і отримуємо «нуль». Перевіривши по таблиці 4.2, бачимо, що значення для немінімізованої функції таке, як і значення в базисі «АБО-НІ».

Аналогічно проводимо розрахунки для обох базисів і для інших тактів.

Результат розрахунків наведено в таблиці А.3.

Отже, проаналізувавши всі розрахунки і таблиці, можемо сказати, що функція, незалежно в якому вигляді, мінімізована чи немінімізована, чи можливо вона в одному з базисів, вона завжди дасть один і той же сигнал за умови, що вона мінімізована правильно.

Головне завдання, яке було поставлене у даному розділі виконано.

В наступному розділі спробуємо промоделювати логічну функцію у вигляді логічних схем.

Даний розділ графічно промоделює нашу логічну функцію. Тобто ми за допомогою диз’юнкторів, кон’юнкторів, інверторів на базі диз’юнктора, чи кон’юнктора спробуємо промоделювати логічну схему у вигляді схеми [3].

Розглянемо деякі елементи які будемо використовувати у даному розділі. Вони подані у таблиці 5.1.

Таблиця 5.1 – Позначення логічних елементів на логічних схемах та

їх опис

Позначення елементу	Опис елементу
	Суматор або дез’юнтор – елемент, який дозволяє отримати логічну суму всіх вхідних аргументів
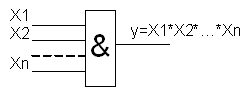
	Кон’юнкторів – логічний елемент, який дозволяє перемножити усі вхідні сигнали.
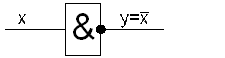
	Інвертор на базі кон’юнкції.
	Інвертор на базі диз’юнкції.
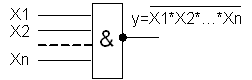
	Елемент логічного множення та інвертування «І – НІ».
	Елемент логічного додавання та інвертування «АБО – НІ».

5.1 Побудова комбінаційної схеми заданої логічної функції

Стоїть завдання побудувати комбінаційну схему функції .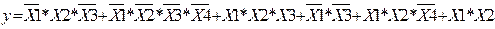

Бачимо, що Х1 та Х2 в інвертованій формі менше ніж Х3 та Х4, тому на вхід схеми подамо 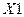, , 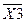та . А як що буде потрібно та 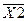, то поставимо інвертор. Схема побудова на рисунку Б.1.

5.2 Побудова комбінаційної схеми мінімізованої функції

Мінімізована функція має вигляд 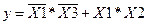, а це набагато простіша функція, а ніж не мінімізована тому вимагає значно меншу кількість сигналів. На вхід подаємо Х2 – прямий сигнал, а на Х1 та Х3 інвертовані значення сигналу, як це показано на рисунок 5.1.

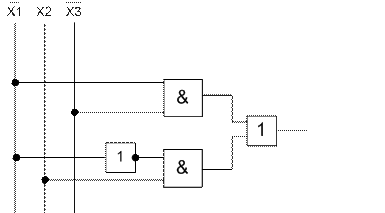
Рисунок 5.1 – Комбінаційна схема мінімізованої функції

5.3 Побудова комбінаційної схеми функції в базисі «І-НІ»

В даній схемі з’являються нові елементи – інвертори на базі кон’юнктора та сам елемент «І-НІ», який наведено в таблиці 5.1. Математична модель даної функції – (3.1). Але складності при побудові схеми в базисі «І-НІ» не виникає. Схема у базисі «І-НІ» представлена на рисунку Б.2.

В даній схемі, для інвертування, використано типовий двох входовий елемент «І-НІ» з об’єднаними входами.

5.4 Побудувати комбінаційну схему мінімізованої функції в базисі «АБО – НІ»

Схема на базисі «АБО-НІ»містить свої елементи такі як: інвертори на базі диз’юнктора і сам логічний елемент «АБО-НІ» останній представлений у таблиці 5.1. Логічний вигляд даної функції подано у моделі (3.2). Побудована схема знаходиться на рисунку Б.3.

Таким чином, у даному підрозділі отримаємо схему, яка використовує 5 елементів «АБО – НІ» з двома входами, причому два з цих елементів використовуються у якості інвертора. Для цього їхні входи об’єднуються.

У наступному розділі буде про модельовано логічну функцію (1.1) у ППП OrCAD, Proteus та Electronic Worcbench. Наступний розділ дасть можливість краще освоїти принципи роботи нашої заданої функції, а саме головне є можливість перевірити правильність розрахунків наведених у попередніх розділах.

Дата добавления: 2015-05-24