
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Моделювання роботи цифрових схем засобами ЕОМ
|
|
|
|
У даному розділі стоїть завдання промоделювати логічну функцію (1.1). Але оскільки ця функція має незручний вигляд, то моделювання буде проведено таким чином. На ПП Proteus промоделюємо два базиси «АБО – НІ» та «І – НІ», у ПП OrCAD – мінімізована функція (2.1), а на Electronic Worcbench залишиться головне завдання промоделювати задану функцію (1.1).
6.1 Аналіз особливостей моделювання у ППП
OrCAD, Proteus та Electronic Worcbench – відомі та популярні програми для моделювання різного роду логічних завдань. Від звичайних електричних кіл до найскладніших схем двійкових сигналів. Мають відміну репутацію, прості у використані і саме головне – полегшують роботу інженера.
Усі програми майже однаково нескладні у використанні, мають велику кількість бібліотек у яких є велика кількість елементів, для створення різного роду схем. Суттєвої різниці між даними ППП нема, але наприклад OrCAD дає можливість моделювати схему при різній тактовій чистоті, а це дає можливість дізнатися при яких сигналах схема буде працювати невірно. Але, все ж найпростішою у використані, на думку більшості споживачів, залишається Electronic Worcbench. З усіх вище представлених ППП він єдиний будує часові діаграми не прикладаючи жодних зусиль. Непотрібно задавати двійковий сигнал. Нарисував схему, підключив до генератора і схема працює.
6.2 Моделювання схем логічних функцій в ППП
У даному підрозділі потрібно промоделювати задану логічну функцію (1.1).
Стоїть задача оволодіти такими ППП, як Proteus, OrCAD, Electronic Worcbench. Для того, щоб краще оволодіти даними ППП, потрібно промоделювати логічну функцію (1.1) і всі її форми.
У ППП Proteus моделюємо два базиси «І – НІ» та «АБО – НІ», у OrCAD – мінімізовану функцію (2.1), а у ППП EWB – буде змодельована функція (1.1).
6.2.1 Моделювання базисів «І – НІ» та «АБО – НІ» у ППП Proteus
Щоб розпочати моделювати кожен із базисів спочатку потрібно пригадати, що функція приведена до будь-якого базису – це функція, яка складається із одного елемента «І – НІ» чи «АБО – НІ». Дані елементи мають трішки інше шифрування у ППП Proteus [6]. Тому для побудови базису «І – НІ» буде використаний елемент «NAND», а для базису «АБО – НІ» – елемент «NOR».
Спочатку проведеться моделювання базису «І – НІ».
Запустивши Proteus, відкриється віко в якому видно робочий лист даної програми (рисунок В.1).
З лівого боку головного вікна ППП розташована панель інструментів, яка містить, разом з іншими, дві кнопки «P» та «L». Для того, щоб виконати пошук необхідних елементів, потрібно натиснути кнопку «P», яка активує вікно, яке проілюстроване на рисунку В.2 у додатку В. В даному вікні обирається необхідний елемент «NAND», який дозволить провести моделювання схеми (див. рис. Б.2, який наведено у додатку Б) в базисі «І-НІ».
Вибраний елемент, відповідно до функції (3.1), необхідно розставити елементи на робочому листі, з’єднати провідниками і під’єднати до генератора. Але перед тим, як приєднатися до генератора спочатку необхідно задати вхідні сигнали (рисунок В.3). Схема складена, до генератора під’єднана, що і показано на рисунок 6.1.
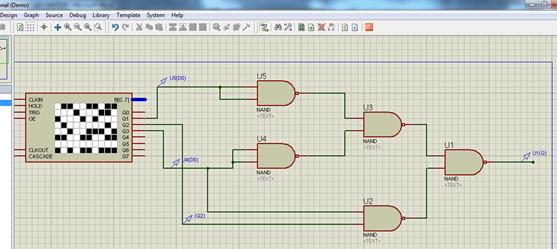
Рисунок 6.1 – Схема базису «І – НІ» у ППП Proteus
На лівій панелі натискаємо на кнопку з графіками. Знизу відкривається меню у якому потрібно вибрати графік типу DIGITAL і на робочому листі мишкою розтягуємо і вказуємо область попереднього графіка. Отримали вікно, яке проілюстроване на рисунку В.4 у додатку В.
Правою кнопкою мишки натискаємо на вікні графіка, випливає вікно (рисунок В.5), у якому обирається команда Add Traces і виконуються
Після того, як виконані дії, що показані на рисунку В.6, потрібно натиснути правою кнопкою миші на графіку і вибирати команду Simulate Graph. Якщо графік вийшов не по всій осі то потрібно редагувати дані генератора. Лівою кнопкою миші два рази натиснути на генератор і поставити дані такі, як на рисунку В.7. Після цього, ще раз, виконуємо команду Simulate Graph. Отримано графік, але у вікні попереднього перегляду, на якому мало що зрозуміло, тому потрібно натиснти правою кнопкою на графіку, після чого відкриється вікно, у якому, потрібно вибрати команду Maximize. Графік розгортається у режим перегляду. Але відразу зрозуміло, що замість шістнадцяти тактів видно в декілька разів більше. Тому, в низу графіка є знак «+» і «-», що відповідає значенням «приблизити» чи «віддалити» відповідно. Натискаємо на «+», доти, поки чітко не видно буде шістнадцять тактів. Кінцева часова діаграма зображена на рисунку В.8.
Схема у базисі «І – НІ» побудована, приступаємо до наступного етапу моделювання схеми у базисі «АБО – НІ». Відкриваємо новий лист Proteus, з ліва натискаємо на кнопку «Р» відкривається теж вікно (див. рис. В.2) тільки замість «NAND» прописуємо «NOR». Складаємо робочу схему підключились до генератора, попередньо задавши вхідний сигнал, і маємо схему базису «АБО – НІ» рисунок 6.2.
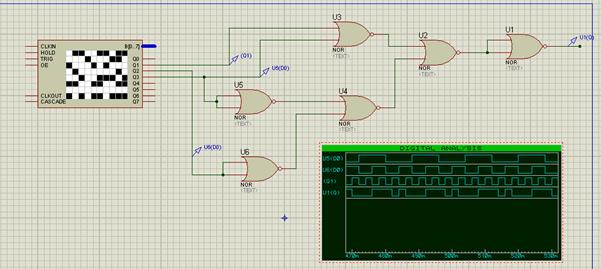
Рисунок 6.2 – Робоча схема базису «АБО – НІ»
Часову діаграму для базису «АБО – НІ» будуємо за тією ж схемою що і для базису «І – НІ». Часова діаграма показана на рисунку В.9.
6.2.2 Моделювання мінімізованої функції у ППП OrCAD
Запускаємо OrCAD, відкривається робочий лист іншої структури, але приблизно з тими ж функціями (рисунок Д.1 у додатку Д). Та перед створенням схеми потрібно створити проект [6].
Для створення проекту потрібно виконати команду File/New/Progect. Далі необхідно виконати все, що зображено на рисунку Д.2. Створивши проект, можна приступати до побудови схеми. В даній програмі меню з елементами, провідниками знаходиться з правої сторони, що і видно на рисунку Д.3. На панелі з права, необхідно вибрати кнопку (схожу на знак логічного елемента) і при натисканні якої, випливе вікно у якому можна вибрати необхідні елементи. Оскільки проводиться модеювання функції (2.1), то видно, що в даній програмі буде використовуватися три різні елементи: логічне множення, логічне додавання, та інвертори. Відповідно їм в OrCAD пропонуються елементи: 7408, 7432, 7404 відповідно. З цих елементів побудована робоча схема, в до якої ще подаємо вхідні та вихідний сигнали. Дана схема запропонована на рисунку 6.3.
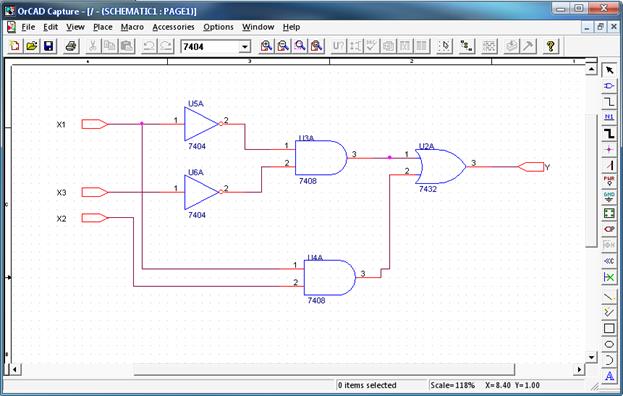
Рисунок 6.3 – Робоча схема у ППП OrCAD
Далі згорнувши робочий лист і активувавши проект, так як показано на рисунку Д.4 (додаток Д), потрібно виконати наступні дії Тools/Annotate, що призведе до появи ще одного вікна, у якому потрібно натиснути «Ок». Наступною командою, яку потрібно зробити, буде Тools/Simulate, після якої знову вікно, у якому потрібно вибрати «In Design» і «Ок».
Відкривається вікно OrCAD Simulate, у якому буде отримана часова діаграма. Для того, щоб отримати часову діаграму потрібно задати вхідні сигнали так, як це показано на рисунку Д.5 додатку Д. Після того, як всі сигнали додано, випливе вікно (рисунок 6.4).

Рисунок 6.4 – Вхідні сигнали діаграми
Наступним кроком буде виконання команди Trace/New Wave Window, появиться вікно, у якому додаються сигнали так, як показано на рисунку Д.6 додатку Д. Після цього пункту потрібно виконати команду Simulate/Run, після чого появиться вікно, у якому потрібно вести проміжок часу, протягом якого будуватиметься часова діаграма, або погодитись із заданим проміжком після чого натиснути «Ок». Часова діаграма побудована і зображена на рисунку Д.7.
6.2.3 Моделювання мінімізованої функції у ППП EWB
ППП EWB – программа, яка призначена для моделювання, аналізу і розрахунку електронних пристроїв на аналогових і цифрових елементах. У даній комп’ютерній програмі стоїть завдання промоделювати логічну функцію (1.1).
Логічна функція – це не мінімізована функція, тому її цифрова схема буде складатися з різних елементів.
Для побудови логічної функції, у ППП EWB, будуть використовуватися елементи, які зображені у таблиці Е.1 (додаток Е). Кожен елементи знаходиться у певному розділі панелі інструментальних кнопок [7]. Логічний Інвертор, логічне множення, логічне додавання знаходиться у розділі Logic Gates, а логічні аналізатор і перетворювач – у розділі Instruments.Отримавши певні знання, можна приступити до моделювання логічної функції.
Елементи логічного множення логічного додавання подаються із двома входами, якщо потрібно три і більше то потрібно виконати наступні дії. Два рази натиснути, лівою кнопкою миші, на потрібному елементі і у вікні, що з’явиться, вибрати закладку Number of Inputs, і там вказати кількість необхідних входів.
Логічний перетворювач – це генератор вхідних сигналів.
Логічний аналізатор – це генератор часових діаграм, тому до нього будуть підключені початки та кінець комбінаційної схеми.
Запустивши комп’ютерну програму EWB, з панелі інструментів вибирається потрібний елемент і простим перетаскуванням миші розміщується у потрібному місті. Комбінаційна схема складається подібно до схеми Б.1 (додаток Б), тільки у ППП EWB подають прямі сигнали і схема матиме трішки інший вигляд. Потім початки приєднують до логічного перетворювача, і до логічного аналізатора. Ще до логічного аналізатора заживлюється кінцевий вивід схеми.
Робоча комбінаційна схема, змодельована у комп’ютерній програмі EWB, зображена на рисунку Е.2 (додаток Е).
Наступним кроком буде відображення у ППП EWB часової діаграми. Якщо у попередніх програмах це було доволі складно, то у даній комп’ютерній програмі це доволі проста операція. Потрібно, лівою кнопкою миші, два рази натиснути на логічному аналізаторі, після чого випливає вікно попередніх часових діаграм. Дане вікно порожне. Для того, щоб у ньому щось з’явилося необхідно включити створену схему, за допомогою перемикача, який знаходиться у правому верхньому кутку робочого листа EWB. Увімкнувши схему, з’являється ще одне вікно з якого, якщо потрібно, можна відразу роздрукувати часову діаграму. Часова діаграма будується у двох вікнах, які зображенні на рисунку Е.3 (додаток Е).
6.3 Визначення мінімальної тривалості вхідних сигналів
Раніше, згадувалося про можливості ППП OrCAD, а точніше про затримки часу, які можна побачити, а потім і визначити із робочої часової діаграми. Та це не головний плюс даної комп’ютрної програми. Вона дає можливість розрахувати критичну частоту, при якій схема буде працювати вірно. Тому на даний підрозділ поставлене завдання, вирахувати критичну частоту роботи схеми, затримки часу по тактам та, якщо можливо, на кожному елементі схеми.
У підрозділі 6.2.2 була змодельована немінімізована логічна функція 2.1. Там була отримана часова діаграма (див. рис. Д.7), яка працювала при частоті: Х1=1600 ns, Х2=800 ns, Х3=400 ns. Для визначення критичної частоти необхідно поступово зменшувати значення Х1, Х2, Х3.
Виконаємо моделювання функції при значеннях: Х1=400 ns, Х2=200 ns, Х3=100 ns. Комп’ютерна програма видала результат, який зображений на рисунку Ж.1 додатку Ж. Проаналізувавши, даний результат можна сказати, що при даній частоті сигналів схема працює вірно.
Коли частоту сигналів зменшити в двічі, то змін у часовій діаграмі не буде видно. Тому проведемо моделювання при чистоті Х1=100 ns, Х2=50 ns, Х3=25 ns. Часова діаграма зображена на рисунку Ж.2. Видно, що часова діаграма працює невірно. Вихідний сигнал появляється лише на шостому такті. При повторені сигналів часова діаграма на два такти включається на одиницю а потім переключається на нуль.
Отже часова діаграма працює невірно, критичну частоту знайдено. Схема вірно працює при частоті Х1=200 ns, Х2=100 ns, Х3=50 ns.
Мінімальну тривалість вхідних сигналів знайдено. Наступне завдання підрозділу полягає у тому, що необхідно знайти часові затримки по тактах та на кожному елементі схеми.
Спочатку необхідно проаналізувати робочу схему ППП OrCAD (див. рис. 6.4). На даній схемі присутні три різні елементи: інвертор, елемент логічного множення та логічного додавання.
Перший елемент приймає один сигнал інвертує його та віддає далі у схему.
Елемент логічного множення включається відразу, як тільки на нього приходить нуль. Якщо одиниця, то він чикає наступного множника і так доти поки на елемент не прийде, хоча б один, нуль, але якщо всі вхідні сигнали мали значення одиниці то елемент включається і на виході маємо одиницю.
Принцип роботи елемента логічного додавання інший. Він навпаки відразу включається лише тоді, коли на нього приходить одиниця, якщо нуль, чикає наступного доданка доти поки не прийде одиниця, але є варіанти коли з усіх входів приходять нулі, то елемент включається відразу після приходу останнього і на виході видає нуль.
Кожен з цих елементів має затримку часу 1τ. Тому логічна схема має два «шляхи» затримки часу 2τ та 3τ, як показано на рисунку Ж.3 у додатку Д. На даному рисунку показано два шляхи проходження сигналу: червоний – 3τ та зелений – 2τ. Довільно взято нульовий такт. Сигнал, як студент, йде найкоротшим шляхом, ним являється другий шлях. На елемент логічного множення прийшов нуль, елемент включився, отримали затримку 1τ. Сигнал не інвертується тому на елемент логічного додавання приходить нуль, елемент не включається. Елемент логічного додавання чикає сигнал з іншого шляху, з першого. Звідти на інвертори приходять нулі перетворюються в одиниці і ці одиниці приходять на елемент логічного множення. Від нього отримали одиницю, яка підходить на елемент логічного додавання після чого схема включається і кінцева відповідь Y=1. Тому, коли перевірити схему, з нульового до п’ятий такт, видно, що схема має затримку 3τ, з п’ятого по сьомий 2τ. Перевіривши, даний практичний розв’язок з прикладом часової діаграми у ППП OrCAD можна сказати, що дійсно з нульового по п’ятий такти отримано одну часову затримку, яка рівна 70 ns, і іншу часову затримку, яка рівна 40 ns. На основі цих даних можна сказати, що затримці 2τ відповідає час 40 ns, а затримці 3τ – 70 ns. Якщо відняти затримку 3τ - 2τ = 1τ, що відповідає затримці часу 30 ns, яка йде на проходження сигналу через інвертор.
Головне завдання розділу виконане. Функція промодельована у різних формах і у різних ППП. За допомогою ППП OrCAD знайдено критичну частоту роботи схеми. З часової діаграми було знайдено затримки часу на тактах і навіть вдалося знайти затримку часу на, одному з елементі, інверторі, яка становить 30 ns.
Наступний розділ буде присвячений мультиплексорові, а значить необхідно буде реалізувати логічну функцію за допомогою мультиплексора.
7 АПАРАТНА МІНІЗАЦІЯ ЛОГІЧНОЇ ФУНКЦІЇ
В даному розділі потрібно реалізувати логічну функцію за допомогою мультиплексора. Мультиплексор дає можливість здійснити передачу інформації, як із одного, так із багатьох інформаційних входів, на вихід. Але, щоб функцію реалізувати за допомогою мультиплексора потрібно спочатку привести функцію до досконалої диз’юнктивної нормальної форми (ДДНФ) та до досконалої кон’юнктивної нормальної форми (ДКНФ) [8]. Що це і для чого буде розказано в підрозділах даного розділу.
7.1 Приведення логічної функції до досконалої кон’юнктивної нормальної форми
При мінімізації логічної функції різними методами наприклад: за допомогою алгебри логіки чи за діаграмами Вейча. Дуже часто отримуються різні але однаково вірні розв’язки. В зв’язку з цим виникає задача знаходження такої форми запису функцій, коли функції відповідає тільки одна формула. Такі форми називають канонічними, або досконалими. Існують ДД і ДК нормальні форми.
Одним із способів приведення функції до ДКНФ є табличний. Він доволі простий у застосуванні. З таблиці істинності 7.1, для трьох змінних, вибираються ті такти на яких логічна функція має значення нуля.
Для заданої логічної функції – це перший, третій, четвертий та п’ятий такти. Значення «Х» додаються, а такти між собою перемножуються. Тому для 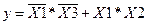 ДКНФ має вигляд:
ДКНФ має вигляд:
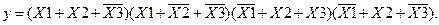 (7.1)
(7.1)
Таблиця 7.1 – Таблиця істинності для трьох змінних
| № | Х1 | Х2 | Х3 | 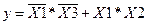
|
Коли говорилося, значення іксів додаються, то потрібно сказати, що додаються вони у прямих та інверсних значеннях. Для ДКНФ прямим значенням є «0», а інверсним «1».
7.2 Приведення логічної функції до досконалої диз’юнктивної нормальної форми
Оскільки, у наступному підрозділі потрібно реалізувати логічні функції (1.1) та (2.1) за допомогою мультиплексора, тому першу краще розв’язати табличним методом, а мінімізовану більш складним методом «методом до множення на недостачу». Спочатку перший метод.
Переглядається і аналізується таблиця істинності для не мінімізованої логічної функції (див. таблицю А.1).
Проаналізувавши потрібно вибрати ті такти по яких функція приймає значення одиниці. Для заданої логічної функції це нульовий, перший, четвертий, п’ятий та з дванадцятого по п’ятнадцятий такти. Кожен з тактів формується за допомогою прямих та інверсних значень «Х», які між собою перемножуються а кожен такт являється доданком ДДНФ. Отже, ДДНФ для логічної функції (1.1) матиме вигляд:
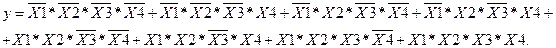 (7.2)
(7.2)
Для ДДНФ прямим є значення «Х=1», а інверсним «Х=0».
Тепер потрібно схожу операцію провести із функцією 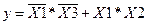 тільки іншим методом. Суть методу недостач полягає у тому, що коли помножити доданок
тільки іншим методом. Суть методу недостач полягає у тому, що коли помножити доданок 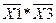 на
на 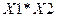 , а
, а 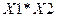 на
на 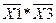 , то отримаємо два доданки, які скоротяться виходячи із формул (1.2). Але просто помножити на недостачу неможна. Потрібно множити на 1 у такому вигляді «
, то отримаємо два доданки, які скоротяться виходячи із формул (1.2). Але просто помножити на недостачу неможна. Потрібно множити на 1 у такому вигляді « » виходячи із формул (1.3). Приведемо логічну функцію до ДДНФ.
» виходячи із формул (1.3). Приведемо логічну функцію до ДДНФ.
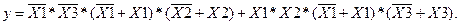 7.3
7.3
Якщо дужки розкрити, то отримується наступне рівняння:
 ……...7.4
……...7.4
Отримане значення є допустимим але не оптимальним. Тому, скрізь, де є у доданках « » або «
» або «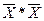 » записується лише одне значення «Х» з формул (1.2). А з донками, які містять «
» записується лише одне значення «Х» з формул (1.2). А з донками, які містять « » записуємо замість них нуль, або взагалі нічого виходячи з формул (1.2). Записуємо остаточний розв’язок ДДНФ:
» записуємо замість них нуль, або взагалі нічого виходячи з формул (1.2). Записуємо остаточний розв’язок ДДНФ:
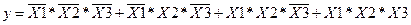 (7.5)
(7.5)
Якщо замінити «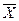 » на «0», а «
» на «0», а «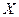 » на «1», то відразу видно, що таке ж саме рівняння можна було б отримати табличним методом.
» на «1», то відразу видно, що таке ж саме рівняння можна було б отримати табличним методом.
До ДДНФ можна приводити функцію двома методами. Очевидно, що метод недостач непоганий і нескладний, але він неактуальний для не мінімізованих функцій. Ним можна приводити функцію до ДДНФ, але навіщо гаяти дорогоцінний час, якщо в кінці виходять абсолютно однакові розв’язки.
7.3 Реалізація логічної функції за допомогою мультиплексора
У даному підрозділі потрібно, спираючись на дані попереднього підрозділу, реалізувати логічну функцію (1.1) та (2.1). Що значить «спираючись»? А значить, що реалізацію функції у мультиплексорі неможна провести без приведення функції до ДДНФ. Тому попередній підрозділ створений недаремно.
Реалізуємо мультиплексор немінімізованої функції, а значить мультиплексор на n адресних (у нашому випадку 4) і 2n інформаційних (16 для заданої функції).
На адресні входи А1, А2, А3, А4 потрібно подавати двійковий сигнал, з таблиці істинності, який відповідає Х1, Х2, Х3, Х4 відповідно. На інформаційні В0, В1, В2,…, В15 подаємо «0» і «1». Але, що і куди подавати? На це питання дає відповідь ДДНФ. Такти, які записано до ДДНФ (доданки), це такти на які подається «1», а на всі інші подаємо нуль. Схема мультиплексора на чотири адресних входи зображена на рисункуК.1.
Теоретично мультиплексор повинен працювати вірно і можна отримати часову діаграму, що зображена на рисунку К.2.
Реалізуємо за допомогою мультиплексора ДДНФ (7.5), схема реалізації показана на рисунку К.3. Як видно даний мультиплексор має лише три адресних і вісім інформаційних сигналів. Тепер потрібно побудувати часову діаграму для даного мультиплексора. Часова діаграма побудована і зображена на рисунку Ж.4. Видно, що часові діаграми схематично однакові.
Задачу поставлену виконано. Функції (1.1) та (2.1) приведені до ДДНФ. Мультиплексор реалізовано, для трьох і чотирьох адресних входів. Часові діаграми побудовано.
В наступному розділі потрібно використовуючи табличний редактор Excel та Visual Basic створити програму, яка буде самостійно розраховувати значення «Y» на заданому такті.
8 РОЗРОБКА ПРОГРАМИ МОДЕЛЮВАННЯ РЕЖИМІВ РОБОТИ СХЕМ
У даному розділі стоїть завдання розрахувати логічну функцію (1.1) у табличному редакторі Excel а в VBA промоделювати мінімізовану функцію 2.1. У табличному реакторові Excel будуть використовуватися стандарті для Excel логічні функції: «И», «ИЛИ», «НЕ». А в середовищі VBA необхідно написати програму, яка буде розраховувати значення функції на такті, який задається.
|
|
|
|
|
Дата добавления: 2015-05-24; Просмотров: 2099; Нарушение авторских прав?; Мы поможем в написании вашей работы!