
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обчислення прибуткового податку 1 страница
|
|
|
|
| Табельний номер | Прізвище та ініціали | Зарплата, грн | Прибутковий податок, грн |
| Z | P | ||
| Котов О.Д. | 1350,00 | ? | |
| Мудрий Л.А. | 2400,00 | ? | |
| Гарна О.Т. | 890,50 | ? |
а) 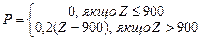
б) 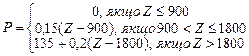
27. Рівень рентабельності виробництва деяких видів продукції
| Продукція | Код | Оптова ціна під-приємства, грн. | Повна собівар-тість, грн. | Рентабельність, % |
| к | о | с | р | |
| шафа КТ | ? | 1407,50 | ? | |
| шафа КТ1 | ? | 1428,00 | ? | |
| шафа КВ3 | ? | 3200,00 | ? |
а) 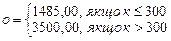 б)
б) 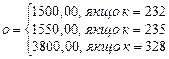
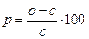
28. Відрахування на амортизацію основних виробничих фондів
| Основні виро- бничі фонди | Вартість фондів, грн. | Відрахування на амортизацію | |
| норма, % | грн. | ||
| k | b | n | a |
| ? | ? | ||
| ? | ? | ||
| ? | ? |
а) 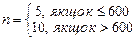 б)
б) 
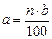
29. Аналіз витрат сировини
| Сировина | Обсяг виробництва | Фактичні витрати | Нормативні витрати | Відхилення |
| о | Vf | Vn | v | |
| пісок | ? | ? | ||
| цемент | ? | ? | ||
| щебінь | ? | ? |
а) Нормативи витрат на одиницю продукції становлять: пісок, щебінь - 0,3, цемент - 0,1.
б) Нормативи витрат на одиницю продукції становлять: пісок - 0,3, цемент - 0,1, щебінь – 0,4.
30. Розрахунок калорійності порції
| Код продукту | Склад порції | Кількість продуктів на 100 порцій | Калорійність |
| Kod | Kilk | Kalor | |
| хліб | 1,5 | ? | |
| масло | 0,7 | ? | |
| ковбаса | 1,2 | ? |
Калорійність 1 порції (Kalor1)?
а) Калорійність хліба – 255, масла, ковбаси – 782.
б) Калорійність хліба – 255, масла - 785, ковбаси – 780.
Розділ 2. Розв'язування інженерних задач
Тема 1. Побудова таблиці значень і графіка функції, що задана прямокутними, полярними координатами і параметрично
Методичні вказівки
Табулювання функції і побудова графіка функції є важливим елементом розв'язання багатьох інженерних задач. ТП Excel дозволяє легко і зручно це робити, причому кількома способами. Важливим є те, що початкові дані можна записати окремо від таблиці, а в таблиці будуть посилання на них. Це дозволяє при зміні початкових даних отримувати автоматичний перерахунок таблиці значень функції і, відповідно, графіка функції. Такий спосіб табулювання функції дає змогу використовувати його як початковий етап для розв'язання інших інженерних задач, зокрема, для знаходження коренів нелінійних рівнянь та ін.
Приклад. Протабулювати функцію 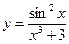 , якщо аргумент х змінюється на проміжку
, якщо аргумент х змінюється на проміжку 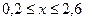 з кроком
з кроком 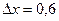 . Спочатку введемо початкові дані: позначимо a, b – межі зміни аргумента х (a= 0,2; b= 2,6 ), dx – крок зміни аргумента х (dx= 0,6 ), n - кількість кроків (n не задано в умові задачі, але ми можемо його обчислити за формулою
. Спочатку введемо початкові дані: позначимо a, b – межі зміни аргумента х (a= 0,2; b= 2,6 ), dx – крок зміни аргумента х (dx= 0,6 ), n - кількість кроків (n не задано в умові задачі, але ми можемо його обчислити за формулою 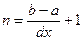 ). Далі потрібно побудувати таблицю значень функції, яка складатиметься з трьох колонок: k – номер кроку (від 0 до n -1, бажано використовувати автозаповнення), x – аргумент функції (обчислюється за формулою
). Далі потрібно побудувати таблицю значень функції, яка складатиметься з трьох колонок: k – номер кроку (від 0 до n -1, бажано використовувати автозаповнення), x – аргумент функції (обчислюється за формулою 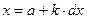 ), y – значення заданої функції. На рис. 1 показано отриманий результат.
), y – значення заданої функції. На рис. 1 показано отриманий результат.
Для побудови графіка функції слід на першому кроці вибрати тип Точечная, на другому кроці – в закладці Ряд задати значення х і у.
У завданні 1 b) задані початкове значення аргумента а, крок зміни аргумента dx і кількість кроків n. Кінцеве значення аргумента можна обчислити за формулою 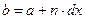 .
.
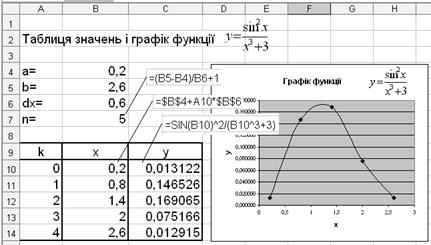
Рис. 1
У завданні 2 функція задана полярними координатами 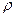 ,
, 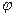 . Таблиця значень
. Таблиця значень 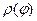 будується так само, як і таблиця значень у(х) у завданні 1. Але для створення графіка потрібно перевести полярні координати у прямокутні, оскільки, серед стандартних діаграм Excel немає графіка функції, що задана полярними координатами. (Підказка:
будується так само, як і таблиця значень у(х) у завданні 1. Але для створення графіка потрібно перевести полярні координати у прямокутні, оскільки, серед стандартних діаграм Excel немає графіка функції, що задана полярними координатами. (Підказка: 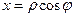 ,
, 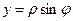 .)
.)
У завданні 3 функція у(х) задана з використанням параметра t: 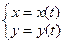 , тому таблиця значень функції складатиметься з чотирьох колонок: k (номер кроку), t (аргумент), x, y.
, тому таблиця значень функції складатиметься з чотирьох колонок: k (номер кроку), t (аргумент), x, y.
Завдання 1. Побудувати таблицю значень і графік функції на вказаному проміжку із заданим кроком зміни аргумента.
1. 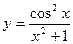 a)
a) 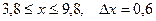 b)
b) 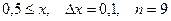
| 2. 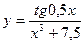 a)
a) 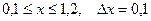 b)
b)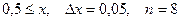
|
3. 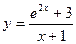 a)
a) 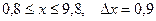 b)
b) 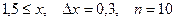
| 4. 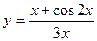 a)
a) 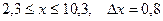 b)
b) 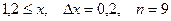
|
5. 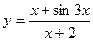 a)
a) 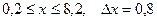 b)
b) 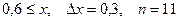
| 6. 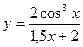 a)
a) 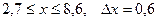 b)
b) 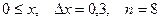
|
7. 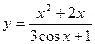 a)
a) 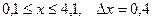 b)
b) 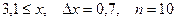
| 8. 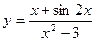 a)
a) 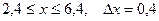 b)
b) 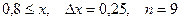
|
9. 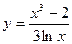 a)
a) 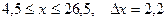 b)
b) 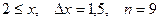
| 10. 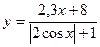 a)
a) 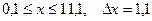 b)
b) 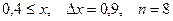
|
11. 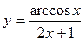 a)
a) 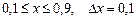 b)
b) 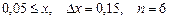
| 12. 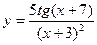 a)
a) 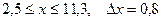 b)
b) 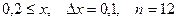
|
13. 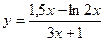 a)
a) 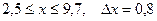 b)
b) 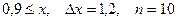
| 14. 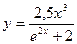 a)
a) 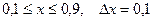 b)
b) 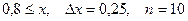
|
15. 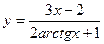 a)
a) 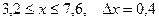 b)
b) 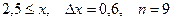
| 16. 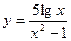 a)
a) 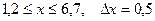 b)
b) 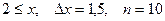
|
17. 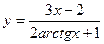 a)
a) 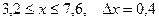 b)
b) 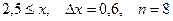
| 18. 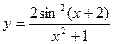 a)
a) 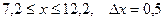 b)
b) 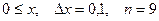
|
19. 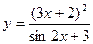 a)
a) 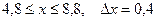 b)
b) 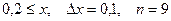
| 20. 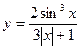 a)
a) 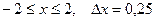 b)
b) 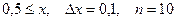
|
21. 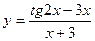 a)
a) 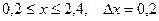 b)
b) 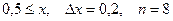
| 22. 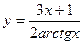 a)
a) 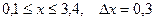 b)
b) 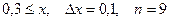
|
23. 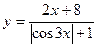 a)
a) 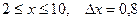 b)
b) 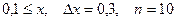
| 24. 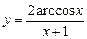 a)
a) 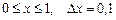 b)
b) 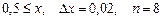
|
25. 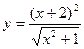 a)
a) 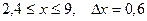 b)
b) 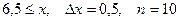
| 26. 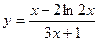 a)
a) 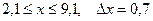 b)
b) 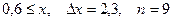
|
27. 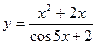 a)
a) 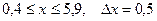 b)
b) 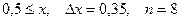
| 28. 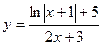 a)
a) 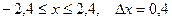 b)
b) 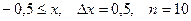
|
29. 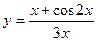 a)
a) 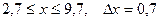 b)
b) 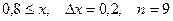
| 30. 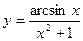 a)
a) 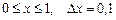 b)
b) 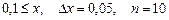
|
Завдання 2. Побудувати таблицю значень і графік функції, що задана полярними координатами. (Порада: проміжок зміни аргумента 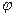 можна задати
можна задати 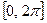 , кількість кроків n=20 .)
, кількість кроків n=20 .)
1. 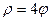
| 16. 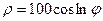
|
2. 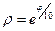
| 17. 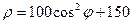
|
3. 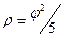
| 18. 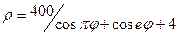
|
4. 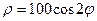
| 19. 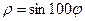
|
5. 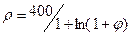
| 20. 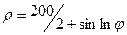
|
6. 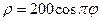
| 21. 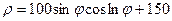
|
7. 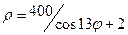
| 22. 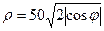
|
8. 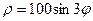
| 23. 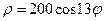
|
9. 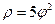
| 24. 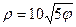
|
10. 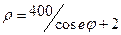
| 25. 
|
11. 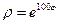
| 26. 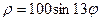
|
12. 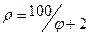
| 27. 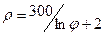
|
13. 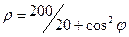
| 28. 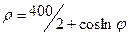
|
14. 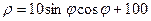
| 29. 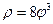
|
15. 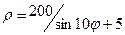
| 30. 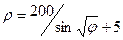
|
Завдання 3. Побудувати таблицю значень і графік функції, що задана параметрично. (Порада: проміжок зміни аргумента t можна задати 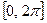 , кількість кроків n=20 .)
, кількість кроків n=20 .)
1. 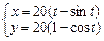
| 16. 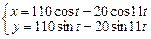
|
2. 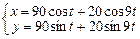
| 17. 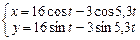
|
3. 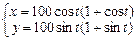
| 18. 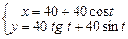
|
4. 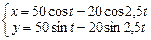
| 19. 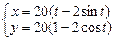
|
5. 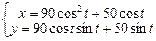
| 20. 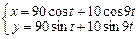
|
6. 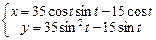
| 21. 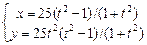
|
7. 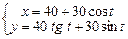
| 22. 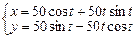
|
8. 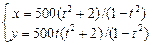
| 23. 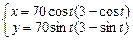
|
9. 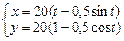
| 24. 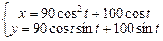
|
10. 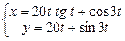
| 25. 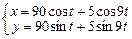
|
11. 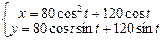
| 26. 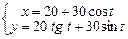
|
12. 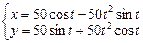
| 27. 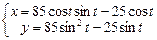
|
13. 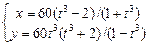
| 28. 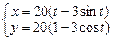
|
14. 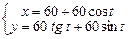
| 29. 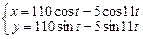
|
15. 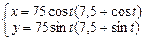
| 30. 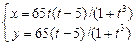
|
Тема 2. Розв'язування нелінійних рівнянь
Методичні вказівки
Для розв'язування нелінійних рівнянь в Excel можна використати такий алгоритм:
1. Звести задане рівняння до виду 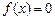 .
.
2. Побудувати таблицю значень функції 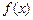 (в таблиці можна задати кількість кроків
(в таблиці можна задати кількість кроків 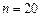 ) і графік цієї функції аналогічно до завдання 1 попередньої теми, обов'язково вказуючи окремо початкові дані.
) і графік цієї функції аналогічно до завдання 1 попередньої теми, обов'язково вказуючи окремо початкові дані.
3. На графіку функції визначити приблизне значення кореня рівняння. Шляхом зміни початкових значень (меж зміни аргумента 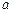 і
і 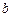 ) уточнити проміжок, де знаходиться корінь.
) уточнити проміжок, де знаходиться корінь.
4. Для знаходження точного аналітичного значення кореня рівняння слід у таблиці значень функції знайти рядок з найменшим за модулем значенням функції (тобто, те значення, яке найближче до 0); рядок можна помітити, наприклад, іншим кольором. Внизу під таблицею ввести значення х з виділеного рядка (лише значення, не формулу!), скопіювати формулу для обчислення функції і виконати процедуру Підбір параметра (меню Сервис ~ Подбор параметра).
Якщо проміжок, де знаходиться корінь рівняння, не заданий, то для побудови таблиці значень і графіка можна задати довільний проміжок, наприклад, 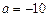 ,
, 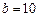 . Далі цей проміжок слід уточнити, зменшуючи або збільшуючи значення
. Далі цей проміжок слід уточнити, зменшуючи або збільшуючи значення 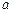 і
і 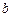 , таким чином, що графік перетинав вісь х у одній точці.
, таким чином, що графік перетинав вісь х у одній точці.
Якщо потрібно знайти кілька коренів рівняння, то слід спочатку задати достатньо великий проміжок зміни аргумента і знайти на графіку та виписати ті проміжки, де знаходяться корені. А потім послідовно виконати п. 3 – 4 (уточнення проміжку і підбір параметра) для кожного кореня.
Завдання 1. Знайти корінь нелінійного рівняння на заданому проміжку
1. 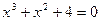 , , 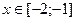
| 2. 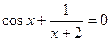 , , 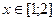
|
3. 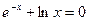 , , 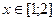
| 4. 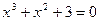 , , 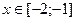
|
5. 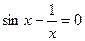 , , 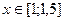
| 6. 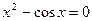 , , 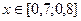
|
7. 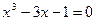 , , 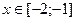
| 8. 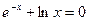 , , 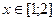
|
9. 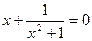 , , 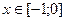
| 10. 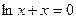 , , 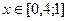
|
11. 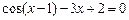 , , 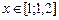
| 12. 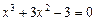 , , 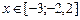
|
13. 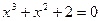 , , 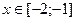
| 14. 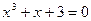 , , 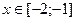
|
15. 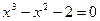 , , 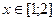
| 16. 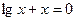 , , 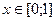
|
17. 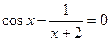 , , 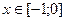
| 18. 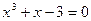 , , 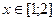
|
19. 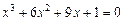 , , 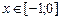
| 20. 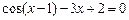 , , 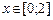
|
21. 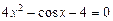 , , 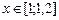
| 22. 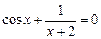 , , 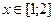
|
23. 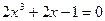 , , 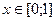
| 24. 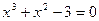 , , 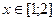
|
25. 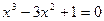 , , 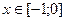
| 26. 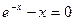 , , 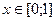
|
27. 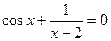 , , 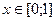
| 28. 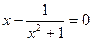 , , 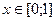
|
29. 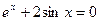 , , 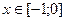
| 30. 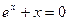 , , 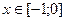
|
|
|
|
|
|
Дата добавления: 2015-05-24; Просмотров: 601; Нарушение авторских прав?; Мы поможем в написании вашей работы!