Модель Уілсона з обмеженнями на складські приміщення

Нехай торговельне підприємство протягом періоду часу Т має завести і реалізувати n видів товару. Введемо наступні позначення:

R_i – повний попит i – го товару за час Т;

C_1i – вартість зберігання однієї одиниці i-го товару планованому періоді часу;

C_Si – витрати із завезення однієї партії i – го товару;

V_i – обсяг складського приміщення займаний однією одиницею i-го товару.

V – вся ємність складського приміщення.

Всі ці значення вважаються заздалегідь відомими. Невідомий поки розмір однієї поставки i-го товару, який позначимо через q_i, а через qio будемо надалі позначати оптимальний розмір однієї поставки i-го товару.
Тоді відповідно до задачі Лагранжа:

f(x)→max

g1 (x)=0; g2 (x)=0; …; gn(x)=0

повні витрати із завезення та зберігання i-го товару будуть рівні:

,

а сумарні витрати з усіх видів товару розраховують за формулою (2.7):

. (2.7)

Далі Vi * q_i – обсяг складських приміщень, який займає i-ий вид товару, åV_i*q_i – обсяг складських приміщень, який займає всі види товару і повинні виконуватися очевидні співвідношення (2.8) та (2.9):

(2.8)

qi £ R_i, q_i ³ 0 (2.9).

Отже, приходимо до задачі Лагранжа, яка полягає у знаходженні мінімуму нелінійної функції:

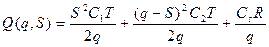
при лінійних обмеженнях (2.8) та (2.9). Функція Лагранжа розглянутої задачі (2.13) – (2.15) має вигляд:

. (2.10)

Функція Лагранжа (2.10) збігається з цільовою функцією (2.7) у випадку якщо в (2.10)

<0 (2.11)

або

>0, ,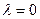

Дата добавления: 2015-05-08