Однопродуктова статична модель з «розривами» цін

В попередніх моделях не враховуються окремі витрати на придбання товарів, так як вони сталі і не впливають на рівень запасу. Однак в багатьох випадках ціна одиниці продукції залежить від розмірів закупленої партії. У таких випадках ціни змінюються стрибкоподібно або надаються гуртові знижки. При цьому в моделі управління запасами необхідно враховувати витрати на придбання.

Розглянемо модель управління запасами з миттєвим збільшенням запасу за відсутності дефіциту. Припустимо, що ціна одиниці продукції дорівнює с₁, при у<q і рівна с₂, при у>q, де с₁>с₂ і q – розмір замовлення, при перевищенні якого надається знижка. Тоді сумарні витрати за цикл, незважаючи на затримки в оформленні замовлення і зберігання запасу, повинні включати затримки придбання.

Сумарні витрати в одиницю часупри у<q становлять:

,

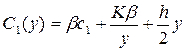а при у>q ці витрати становлять:

.

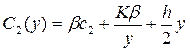Графіки цих двох функцій наведені на рис. 2.5. Нехтуючи впливом зниження цін, позначимо через у _т розмір замовлення, при якому досягається мінімум величин С ₁ і С₂.

Тоді у _т = .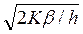

Алгоритм визначення у ^* має наступні основні кроки:

Крок 1. Визначити у_{т = 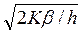,} якщо q < у_т, то q знаходиться взоні І, тоді у*= у_т. В іншому випадку перейти до кроку 2.

Крок 2. Визначити q ₁ з рівняння C₁(y_т)=C(q₁) і встановити, де саме відносно зон II і Ш знаходиться значення q.

а) Якщо у_т 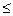q q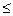₁ (зона II), то у* = q.

б) Якщо q 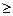q₁ (зона III ), то у* =у_т.

С₁

С

y

Мінімум

q y_m q₁

Рисунок 2.6. - Модель з розривами цін.

У будь-якій задачі управління запасами вирішується питання вибору розмірів і термінів розміщення замовлень на продукцію. На жаль, спільне рішення цих завданнь неможливо одержати на основі однієї моделі. Тому розроблені найрізноманітніші моделі, що описують різні окремі випадки. Одним з вирішальних факторів при розробці моделі управління запасами є характер попиту. У найбільш простих моделях передбачається, що попит є статичним детермінованим.

Ми проаналізували такі моделі управління запасами: модель Уілсона без обмежень та з обмеженнями на складські приміщення, однопродуктову статичну модель, однопродуктова статичну модель з «розривами» цін. У більшості розглянутих моделей управління запасами здійснюється оптимізація функції витрат, що включає витрати на оформлення замовлень, закупівлю і зберігання продукції, а також втрати від дефіциту. Втрати від дефіциту зазвичай найбільш складно оцінити, тому вони можуть бути обумовлені такими нематеріальними факторами, як, наприклад, погіршення репутації. З іншого боку, хоч оцінку витрат на оформлення замовлення отримати неважко, включення в модель цієї статті витрат істотно ускладнює математичний опис завдання.

Відомі моделі управління запасами рідко точно описують реальну систему. Тому рішення, що отримується на основі моделей цього класу, слід розглядати скоріше як принципові висновки, а не конкретні рекомендації

Дата добавления: 2015-05-08