Однофакторний дисперсійний аналіз

Дисперсійний однофакторний аналіз використовується у дослідженнях зміни результативної ознаки під впливом зміни умов або градацій фактора. Суть математичних перетворень дисперсійного методу полягає в тому, щоб зіставити дисперсії за факторами із дисперсією усіх значень, отриманих в експерименті. Однофакторний аналіз вимагає не менше трьох градацій фактора і не менше двох випробовувань у кожній градації. При проведенні дисперсійного аналізу необхідно перевірити нормальність розподілу досліджуваної випадкової величини і відсутність відмінності дисперсій сукупностей. Це можна виконати методами перевірки статистичних гіпотез. Розглядається дія одиничного фактору А (кількісного чи якісного), котрий приймає k різних значень (рівнів фактора). Найпростіші розрахунки виходять при рівній кількості дослідів на кожному рівні фактора А.

Вихідні дані для однофакторного дисперсійного аналізу з рівним числом паралельних дослідів
Номер досліду	Рівні фактору
...	...	...	...	...
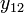
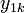
n			...

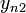
Дисперсійний аналіз можна провести за наступним алгоритмом:

1. Обчислити:

a. суми за стовпцями: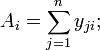

b. суму квадратів усіх дослідів: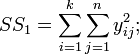

c. суму квадратів сум за стовпцями, поділену на число дослідів в стовпці:

d. квадрат загальної суми, поділений на число всіх дослідів (коректуючий член):

e. суму квадратів для стовпчика:

f. загальну суму квадратів, рівну різниці між сумою квадратів всіх дослідів та коректуючим членом:

g. залишкову суму квадратів для оцінки помилки експерименту:

h. дисперсію : ;

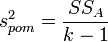i. дисперсію: : ;

2. Результати розрахунків представити у вигляді таблиці дисперсного аналізу:

Вихідні дані для однофакторного дисперсійного аналізу з рівним числом паралельних дослідів
Джерело дисперсії	Число ступенів вільності	Сума квадратів	Середній квадрат	Математичне сподівання середнього квадрату
Залишок
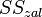
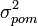
Загальна сума

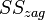
Якщо 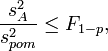то вплив фактора слід вважати незначним. При цьому загальна дисперсія пов’язана тільки з фактором випадковості і може служити оцінкою для дисперсії відтворення. Така оцінка краща від , бо має більше число степенів вільності. Якщо ж справедлива нерівність

де та , різниця між дисперсіями та значна і, відповідно, значний вплив фактора .

Дата добавления: 2015-05-24