Деякі відомості з теорії квадратичних форм

В цьому параграфі ми розглянемо деякі питання теорії квадратичних форм, які нам будуть потрібні надалі.

Означення 2.1 Функція

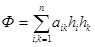, а_іk=а_kі=сonst, (2.1),

яка залежить від змінних h₁, h₂,…, h_n, називається квадратичною формою від вказаних змінних.

Означення 2.2 Квадратична форма називається додатньо визначеною (від’ємно визначеною), якщо при будь-яких значеннях h ₁, h₂,…, h_n, одночасно не рівних нулю, вона набуває додатніх (від’ємних) значень.

Додатньо визначені та від’ємно визначені форми називаються знаковизначеними.

Означення 2.3 Квадратична форма називається знакозмінною, якщо вона приймає як додатні так і від’ємні значення.

Означення 2.4 Квадратична форма називається квазізнаковизначеною, якщо вона приймає лише недодатні або лише невід’ємні значення, але при цьому вона дорівнює нулю при деяких h ₁, h₂,…, h_n, які одночасно не дорівнюють нулю.

Сформулюємо критерій Сільвестера знаковизначеності квадратичних форм.

Симетричну матрицю 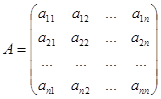будемо називати матрицею квадратичної форми (2.1). Визначники А ₁ =а ₁₁, ,..., називаються головними мінорами матриці А квадратичної форми.

Теорема 2.1 Для того, щоб квадратична форма (2.1) була додатньо визначеною необхідно і достатньо, щоб виконувалися нерівності:

А ₁ >0, A₂>0,…, A_n>0 (2.2).

Для того, щоб квадратична форма була від’ємно визначеною необхідно і достатньо, щоб знаки головних мінорів А ₁, А₂,..., А_п чергувалися, причому А ₁ >0.

Очевидно диференціал другого порядку функції U=f(x ₁, x₂,…,x_n) в точці М₀(х⁽⁰⁾ ₁ ,...,х⁽⁰⁾_п) є квадратичною формою змінних Dх ₁, Dх₂,...,Dх_п.

Для формулювання достатніх умов існування екстремуму функції багатьох змінних використовуються квадратичні форми.

Дата добавления: 2015-05-24