Умовний екстремум

Часто в математиці зустрічаються задачі пов’язані з відшуканням екстремуму функції, аргументи якої задовольняють додатковим умовам зв’язку. Екстремуми такого типу називаються умовними.

Розглянемо приклад. Знайти екстремуми функції U=x²+y² при умові, що х і у задовільняють умові зв’язку х+у- 1 = 0. Таким чином ми шукаємо екстремум функції не на всій площині, а лише на прямій х+у- 1=0. Для розв’язання цієї задачі в рівняння функції U=x²+y² підставляємо значення y=-x+ 1, знайдене з рівняння зв’язку. Цим самим ми звели поставлену перед нами задачу до задачі про відшукання звичайного екстремуму функції U=2x²-2x+ 1. Оскільки похідна U¢=4x-2 дорівнює нулю при х= 1/2 і U¢¢( 1/2 )= 4>0, то при х= 1/2 дана функція має мінімум, який дорівнює 1/2. Таким чином функція U=x²+y² при умові зв’язку х+у- 1 = 0 має умовний мінімум U= 1/2 в точці (1/2; 1/2). Слід відмітити, що мінімум функції досягається в точці (0,0) і дорівнює 0.

Перейдемо до загальної задачі про відшукання умовного екстремуму. Нехай треба знайти екстремум функції т+п змінних.

U=f(y ₁ ,y₂,…,y_m,x ₁ x₂,…,x_n) (4.1)

При наявності т -умов зв’язку

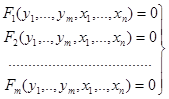(4.2)

Означення 4.1 Будемо говорити, що в точці М₀ (у ₁⁽⁰⁾,..., у_т ⁽⁰⁾ ,х ₁⁽⁰⁾,..., х_п ⁽⁰⁾) координати якої задовольняють умовам зв’язку (4.2), функція (4.1) при наявності зв’язків (4.2) має умовний максимум (мінімум), якщо існує окіл цієї точки такий, що для всіх точок М з даного околу, координати яких задовольняють рівнянням зв’язку (4.2), виконується нерівність: f(M)£f(M₀) (f(M)³f(M₀)).

Для знаходження умовного екстремуму функції (4.1) при наявності зв’язків (4.2) припустимо, що функції, які стоять в лівих частинах рівностей (4.2) диференційовані в деякому околі точки М₀, при цьому частинні похідні цих функцій по змінних у ₁ ,...,у_т неперервні в цій точці і якобіан

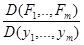(4.3)

не дорівнює нулю. В цьому випадку внаслідок теореми (3.1) (розділу 4 цієї частини) існують додатні числа e ₁ ,...,e_т і окіл точки М₀(х ₁ ⁽⁰⁾,...х_п⁽⁰⁾) такий, що в цьому околі визначені т функцій

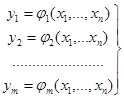(4.4),

які задовільняють умови ½ у ₁ -у ₁ ⁽⁰⁾ ½< e ₁,...,½ у_т-у_т⁽⁰⁾ ½< e_m і які є єдиним диференційованим розв’язком системи (4.2).

Підставивши знайдені функції (4.3) в (4.1) ми зводимо нашу задачу про існування умовного екстремуму до задачі про існування звичайного екстремуму функції.

U=f(j ₁ (x ₁ ,…,x_n),…,j_m(x ₁ ,…,x_n), x ₁ ,…,x_n,)=Ф(х ₁ ,...,х_п) (4.5).

Розглянемо, як не знаходячи розв’язків системи (4.2) можна встановити необхідні умови існування умовного екстремуму в точці М₀. Нехай функція диференційовна в точці М₀ і має умовний екстремум при наявності зв’язків (4.2) або те саме, що функція (4.5) має звичайний екстремум в точці М₀. Звідси слідує, що 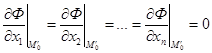, а значить

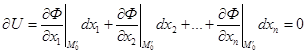(4.6)

при довільних дх ₁ ,...,дх_п. На основі інваріантності форми диференціала формулу (4.6) можна записати можна записати наступним чином:

(4.7)

(при цьому частинні похідні беруться в точці М₀). Зазначимо, що dy ₁ ,dy₂,…,dy_m є диференціалами функцій (4.4) і тому рівність (4.7) не є тотожністю відносно цих диференціалів. Якщо в рівняння зв’язку (4.2) замість у ₁ ,...у_т підставити функції (4.4) то одержимо тотожності. Диференціюючи їх одержимо 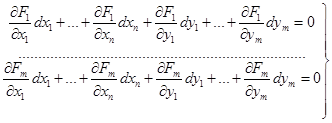(4.8).

Так, як якобіан (4.3) не дорівнює нулю в точці М₀, то з цієї системи можна знайти dy ₁ ,…,dy_m. Вони є лінійними функціями відносно dx ₁ ,…,dx_n, якщо знайти ці вирази і підставити в (4.7), то одержимо:

А ₁ dx ₁ +…+A_ndx_n=0, (4.9)

де А ₁ ,...,А_п виражаються через частинні похідні f, F ₁ ,…,F_m в точці М₀. Так, як в (4.9) фігурують тільки диференціали незалежних змінних, то А ₁ =А₂=...=А_п=0. Приєднуючи до цих рівностей т умов зв’язку (4.2), одержимо необхідну умову існування умовного екстремуму, яку записують у такому вигляді:

А ₁ =0,..., А_п=0, F ₁ =0,…,F_m=0 (4.10),

що являє систему т+п рівнянь з т+п невідомими.

При знаходженні точки можливого умовного екстремуму методом, який ми розглянули, часто виникають труднощі, зв’язані з тим, що частина змінних х ₁ ,...,х_п розглядаються нами, як незалежні, а інші – як функції від цих змінних. Лагранж запропонував метод, який спрощує цю незручність. Розглянемо функцію:

Y(у ₁ ,...,у_т,х ₁ ,...,х_п)=f(у ₁ ,...,у_т,х ₁ ,...,х_п)+l ₁ F ₁ (у ₁ ,...,у_т,х ₁ ,...,х_п) +…

…+ l_mF_m (у ₁ ,...,у_т,х ₁ ,...,х_п) (4.11),

де l _{1 ,...,} l_т – довільні сталі. Цю функцію називають функцією Лагранжа. Легко бачити, що якщо рівність (4.8) помножити відповідно на l _{1, ...,} l_т і одержані рівності скласти почленно з рівнянням (4.7), то одержаний результат можна записати у вигляді:

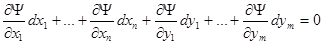(4.12).

Так, як при наявності зв’язків (4.2) F(M)-F(M₀)=Y(M)-Y(M₀) екстремуми функцій (4.3) і (4.11) співпадають. Підберемо l₁,...,l_т так, щоб

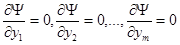(4.13).

Це можна зробити бо ці рівності приводять до лінійної системи рівнянь відносно l ₁ ,...,l_т

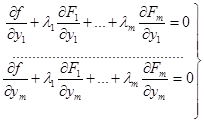
визначник якої рівний якобіяну (4.3), відмінний від нуля. При таких l ₁ ,...,l_т рівність (4.12) матиме вигляд

(4.14).

Оскільки х ₁ ,...,х_п – незалежні змінні, то з (4.14) слідує, що

(4.15).

Приєднавши до рівнянь (4.13) і (4.15) умови зв’язку (4.2), ми одержимо систему п+2т рівнянь

(4.16)

для визначення п+т координат точки умовного екстремуму і множників l ₁ ,...,l_т.

Практично для реалізації цього методу поступають наступним чином: складають функцію Лагранжа і для неї знаходять точки можливого звичайного екстремуму. Для виключення l ₁, ...,l_т застосовують умову зв’язку.

Розглянемо один із шляхів дослідження точок можливого умовного екстремуму. Припустимо, що в точці М₀ виконуються необхідні умови умовного екстремуму (4.16). Крім цього, нехай в деякому її околі функції (4.1) і (4.2) - двічі диференційовані і всі частинні похідні другого порядку – неперервні в точці М₀. Так, як при наявності зв’язків (4.2) екстремуми функцій U=f(y ₁ ,…,y_m,x ₁ ,…,x_n) і Лагранжа співпадають, то з результатів параграфу де розглядалися достатні умови існування екстремуму слідує, що якщо при наявності умов зв’язку (4.2) другий диференціал d²Y в точці М₀ є додатньо визначеною квадратичною формою, то в точці М₀ функція має умовний мінімум, а якщо d²Y є від’ємно визначеною квадратичною формою, то функція має умовний максимум.

Зазначимо, що другий диференціал d²Y в точці М₀ можливого умовного екстремуму можна вираховувати так, якби всі змінні x ₁ ,…,x_n,y ₁ ,…,y_m були незалежними. Дійсно:

.

Але, оскільки, 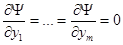, то

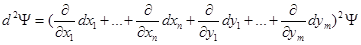(4.17).

Оскільки нам потрібно встановити знаковизначеність d²Y при наявності зв’язків (4.2), то в формулу (4.17) замість dy ₁ ,…,dy_m потрібно підставити іх значення, знайдені з системи (4.8) і після цього досліджувати знаковизначеність квадратичної форми d²Y.

Розглянемо приклад. Знайти умовні екстремуми функції: U=x ₁ ^m+…+x_n^m, якщо х ₁ +...х_п=па, а>0, n> 1.

Складаємо функцію Лагранжа . З системи

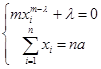
знаходимо l=-та^{т- 1} і координати х_і=а, точки М₀ можливого екстремуму. Знаходимо другий диференціал d²Y функції , . В точці М₀(а,...,а) . Так, як d²Y(a,…,a)>0, то в точці М₀ функція U має мінімум, U_min=na^m.

Частина III. Розробка електронного посібника “Елементи функціонального аналізу та диференціальне числення функцій багатьох змінних”

У час активного наукового розвитку, актуальною є проблема вибору таких засобів навчання, які б давали найкращі результати. Перехід на кредитно-модульну систему дав поштовх до використання нового навчально-методичного забезпечення.

Якщо в традиційній освітній системі навчання проходить шляхом читання книг, то сьогодні з'явилося багато інших методів. Особливістю сучасного педагогічного процесу є те, що на відміну від традиційного навчання, де центральною фігурою є вчитель, викладач, центр тяжіння при використанні інформаційних технологій поступово переноситься на учня, студента, який активно будує свій навчальний процес, вибираючи власний напрям в розвинутому навчальному середовищі. Важливою функцією викладача при цьому є підтримка студента в його діяльності: сприяти його успішному руху в морі навчальної інформації, полегшувати вирішення проблем, що виникають, допомагати в освоєнні великої за обсягом інформації.

Таким чином, в даний час з різних предметів існують електронні підручники. Розробники підручників такого типу намагаються широко використовувати специфіку віртуального середовища з ціллю підвищення ефективності самостійної роботи школярів і студентів з навчальним матеріалом. У новому інформаційному середовищі реалізується варіативний характер планування діяльності з вивчення даної теми, диференціюються рівні її освоювання, забезпечується оперативне орієнтування в структурі навчального тексту, використовуються різноманітні пошукові системи, представлені динамічні малюнки і відеосюжети, існує звуковий супровід візуальної інформації, має місце моніторинг навчальних успіхів учня, студента в роботі над кожною темою, а також контроль якості набутих ними знань і умінь.

Є ряд навчальних технологій, які сьогодні існують і можуть бути реалізовані в електронному навчальному посібнику. Структура і зміст електронного підручника, його функціональні можливості повинні підтримувати:

1. технологію формування у користувачів основних елементів структури наукового знання (фактів, понять, законів, теорій, наукової картини світу);

2. технологію формування загальних знань і навичок роботи користувачів з навчальною інформацією, представленою як у традиційній навчальній книзі, так і в електронній версії:

v Вміння працювати з блоками інформації, які мають різну знакову форму представлення:

· текстом

§ виділяти головне, істотні елементи його змісту;

§ систематизувати і узагальнювати інформацію (встановлювати зв'язок між його основними елементами);

§ користуватися раціональними способами наочної фіксації головного в змісті, способами візуального відображення структури прочитаного (конспект, план-конспект, тезиси, опорний конспект, схеми, таблиці тощо);

· науковою символікою;

· графіками;

· схемами, таблицями (в тому числі електронними), діаграмами;

· малюнками;

· фотознімками;

· анімаційними (або числовими) моделями.

v Вміння працювати з апаратом орієнтування, тобто раціонально користуватися:

· змістом;

· анотацією, вступом, висновками;

· предметним, іменним та іншими покажчиками, словниками тощо;

· бібліографічним списком;

· системою додатків;

· системою „навігатор” і пошуковими системами в віртуальному середовищі.

v Вміння працювати з апаратом засвоєння матеріалу:

· систематизуючими таблицями і схемами, які ілюструють структуру інформації;

· прикладами, що відображають досвід застосування інформації в розв’язанні конкретних задач;

· системою задач і запитань для самостійної роботи над матеріалом і самоконтролю якості його засвоєння.

v Вмінням користуватися книгою (інформаційною системою ПК і її інструментальними можливостями) з метою підготовки:

· успішного виступу;

· письмової роботи:

§ рецензії, анотації;

§ реферату;

§ тез.

3. технологію контролю якості знань і вмінь користувачів;

4. технологію розвитку творчих здібностей в процесі роботи з навчальною інформацією.

Інтерактивний характер електронного підручника та інструментальні можливості ПК дозволяють реалізувати дані технології навчання на найвищому рівні ефективності з точки зору їх освітнього характеру.

Надзвичайно важливий пошук нових конструктивних підходів до розробки електронного підручника, які дозволяють зробити цей підручник інформаційно більш об’ємним і процесуально більш ефективним по відношенню не тільки до традиційного паперового варіанту, але і до існуючих його віртуальних версій.

У ході виконання дипломної роботи нами створений такий навчальний посібник, який містить курс математичного аналізу.

Дата добавления: 2015-05-24