Вказівки до виконання роботи. Мета роботи:дослідитизакономірностіскладних рухів абсолютно твердих тіл та закони, що їх описують: закони динаміки поступального та обертального руху

Лабораторна робота № 1.3. Вивчення закономірностей руху маятника Максвела та визначення його моменту інерції

Мета роботи: дослідитизакономірностіскладних рухів абсолютно твердих тіл та закони, що їх описують: закони динаміки поступального та обертального руху, закон збереження механічної енергії; визначити на їхній підставі момент інерції тіла.

Для виконання роботи треба засвоїти такий теоретичний матеріал: кінетична та потенціальна енергії, закон збереження енергія, центр мас, закон руху центра мас, обертання твердого тіла, момент сили, основне рівняння динаміки обертального руху, момент інерції, плоский рух абсолютно твердого тіла.

Література: [ 1, т.1 §§ 3.2, 3.3, 4.2, 4.3, 4.4, 2, §§ 12, 13, 16, 17, 18; 6, §§ 2.2.3, 2.3.3, 2.5.1, 2.5.2, 2.5.3; 7, §§ 1.3, 1.4]

Перед виконанням ознайомитись з вказівками до роботи № 1.1.

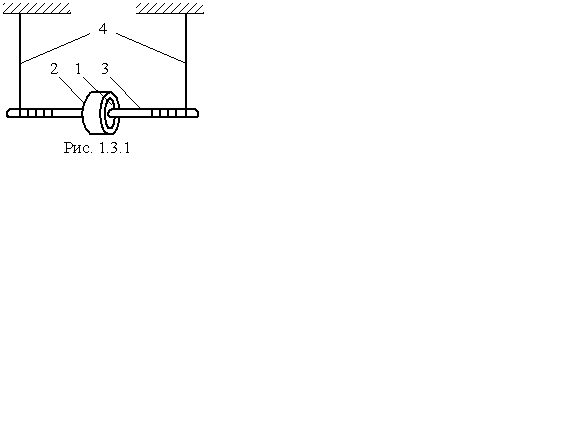
Маятник Максвелла (рис. 1.3.1) – це диск (1) з кільцем (2), насаджений на стрижень (3), на який намотані нитки (4). Диск маятника являє собою безпосередньо сам диск і змінні кільця, які закріплюються на ньому. Маятник в зафіксованому верхньому положенні має потенціальну енергію:

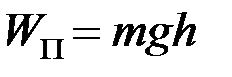. (1.3.1)

Оскільки потенціальна енергія визначається з точністю до адитивної константи, за її нульовий рівень обрано положення, коли маятник знаходиться в нижньому положенні (в положенні, коли нитки повністю розмотані).

Після звільнення маятника диск починає рухатись. Рух маятника – це складний рух, який є суперпозицією поступального руху центра мас та обер-
тального руху навколо осі, що проходить через центр мас і перпендикулярна до площини, у якій він рухається. Такий рух називається плоским рухом.

Потенціальна енергія маятника під час його руху перетворюється на суму кінетичної енергії його поступального руху та кінетичної енергії обертального руху в деякій точці траєкторії:

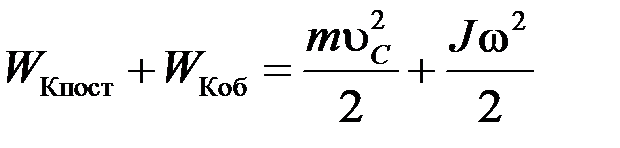,(1.3.2)

де 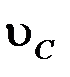– швидкість руху центра мас маятника, – кутова швидкість його обертання, m – маса маятника, J – момент інерції маятника відносно осі, яка проходить через його центр мас (про визначення моменту інерції див. лаб. роб. 1.1).

Якщо тертям знехтувати, то згідно із законом збереження енергії потенціальна енергія, яку маятник мав у найвищій точці відносно нульового рівня, перетворилась на кінетичну енергію в найнижчій точці:

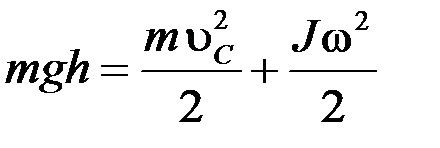. (1.3.3)

Після потрапляння маятника у найнижчу точку (коли нитки розмотані) завдяки інерції відбувається намотування ниток на стрижень, що призводить до подальшого підйому маятника вгору. Унаслідок підйому рух маятника вповільнюється, маятник зупиняється, а потім знову починає свій рух вниз. Такий процес відбувається з деякою періодичністю, завдяки чому це тіло і називається, власне, маятником.

Прискорення поступального руху центру мас маятника а_С може бути визначене за допомогою формул кінематики, тобто для його розрахунку достатньо виміряти час τ, за який маятник проходить відстань h:

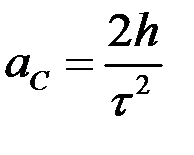. (1.3.4)

Знаючи лінійне прискорення центра мас а_С та його кутове прискорення 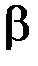, яке визначається із формул зв’язку кутових та лінійних величин так:

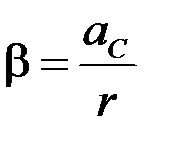, (1.3.5)

де r – радіус осі маятника, можна знайти кутову швидкість його обертання ω в найнижчій точці згідно з кінематичними рівняннями:

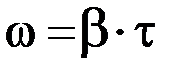(1.3.6)

та швидкість центра мас маятника в цій точці:

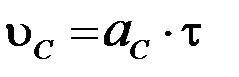. (1.3.7)

Підставимо формули (1.3.4) – (1.3.7) в формулу (1.3.3) та виразимо з останньої величину моменту інерції:

.

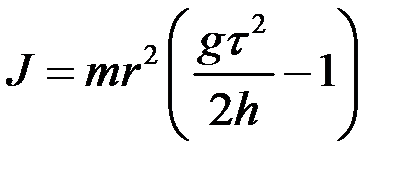Аналогічну формулу отримано на підставі законів динаміки поступального та обертального рухів в лабораторній роботі 1.1.

Зважаючи на те, що радіус осі 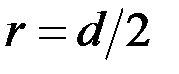(d – діаметр осі), а маса маятника m є сумою мас його частин 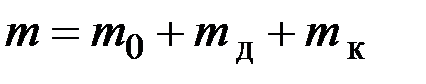(де m ₀ – маса осі, m _д – маса диска і m _к – маса кільця), маємо:

.

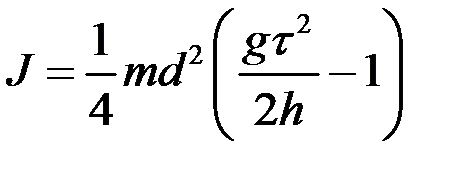Оскільки величина 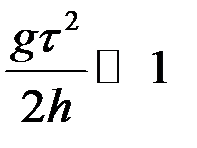, то остаточно отримаємо:

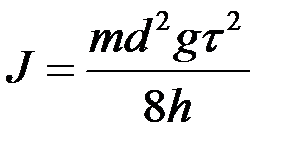. (1.3.8)

З другого боку, формулу для визначення моменту інерції маятника Максвелла можна також отримати за допомогою законів динаміки поступального та обертального рухів, оскільки маятник здійснює плоский рух, який є суперпозицією поступального і обертального рухів.

Момент інерції маятника Максвелла, як симетричного тіла, можна також обчислити, знаючи його геометричні розміри, за формулою:

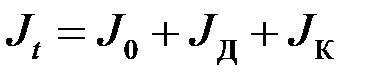, (1.3.9)

де 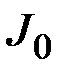, , 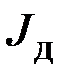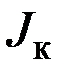– відповідно моменти інерції осі, диска й кільця маятника.

Момент інерції осі 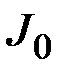маятника дорівнює:

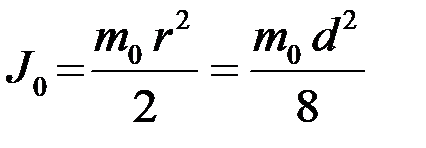. (1.3.10)

Момент інерції диска 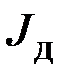може бути знайдений як:

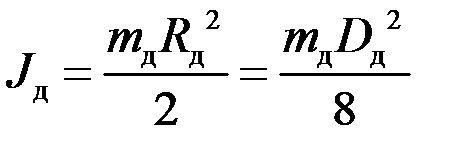, (1.3.11)

де R _д – радіус диска; D _д – діаметр диска.

Момент інерції кільця 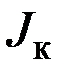розраховують за формулою:

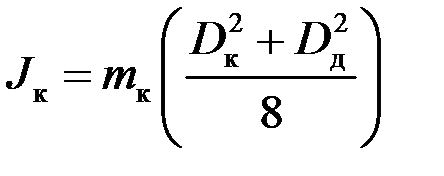, (1.3.12)

де D _к – зовнішній діаметр кільця.

Підставляючи формули (1.3.10) – (1.3.12) в (1.3.9), остаточно маємо:

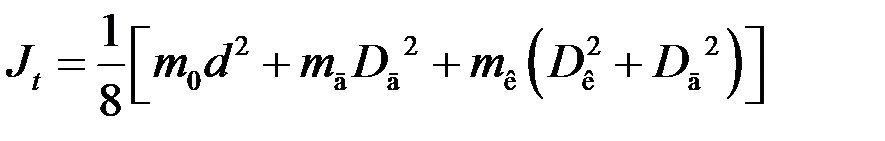. (1.3.13)

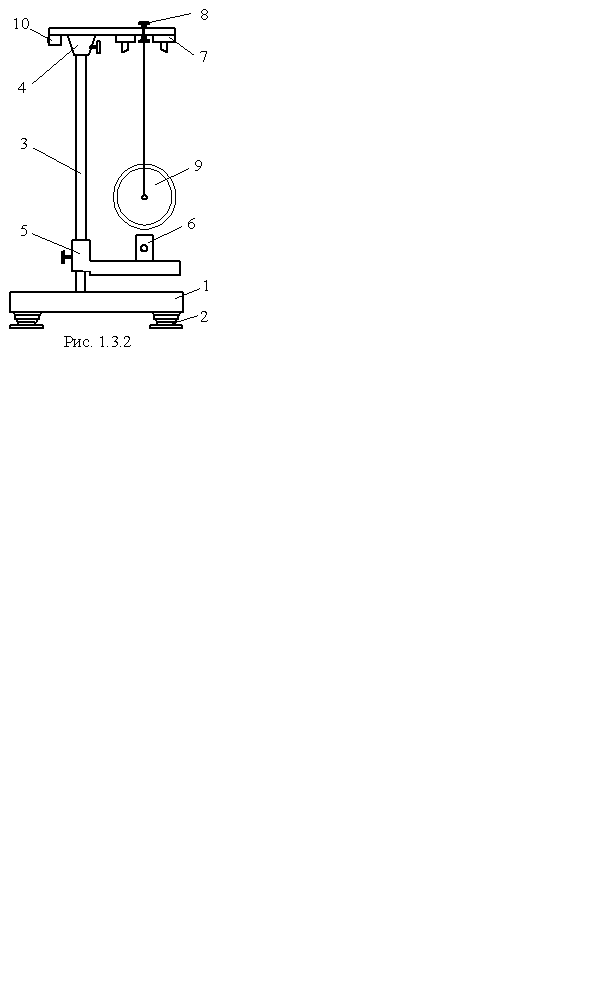Загальний вигляд установки показано на рис. 1.3.2. Підставка (1) оснащена регульованими ніжками (2), які дають змогу вирівняти прилад. На підставці закріплена стійка (3), до якої прикріплений нерухомий верхній кронштейн (4) і рухомий нижній кронштейн (5) із фотоелектричним датчиком (6). На верхньому кронштейні знаходиться електромагніт (7) і воротки (8) для закріплення й регулювання довжини біфілярної підвіски маятника (9). Маятник з накладеним кільцем утримується у верхньому положенні електромагнітом. Довжину маятника визначають за допомогою лінійки. Для вимірювання часу опускання маятника на підставці (10) закріплений секундомір, який автоматично вмикається в разі вимкнення електромагніта.

Дата добавления: 2015-05-24