Вказівки до виконання роботи. Контрольні запитання

Лабораторна робота № 1.4. Вимірювання пружних характеристик МАТЕРІАЛІВ

Контрольні запитання

1. Що являє собою маятник Максвелла? Який рух він здійснює?

2. Що називають моментом інерції точки (тіла або системи точок) відносно осі обертання?

3. Сформулюйте закон збереження механічної енергії.

4. Як визначається кінетична енергія поступального та обертального руху абсолютно твердого тіла?

5. Який рух називають плоским рухом абсолютно твердого тіла?

6. На основі закону збереження енергії отримайте формулу для визначення моменту інерції маятника Максвелла.

7. Як розрахувати момент інерції маятника Максвелла, відповідно до його геометричних розмірів?

8. Виведіть формулу для визначення моменту інерції маятника Максвелла на підставі законів динаміки поступального та обертального руху абсолютно твердого тіла.

Мета роботи: дослідити закономірності пружної деформації твердих тіл; визначити залежність деформації стального дроту від діючої сили та обчислити модуль Юнга.

Для виконання роботи потрібно засвоїти такий теоретичний матеріал: пружні сили, закон Гука; потенціальна енергія системи; консервативні сили; енергія пружної деформації.

Література: [ 2. §21; 3. т.1 §14, 21, 25; 6, §§ 2.6.1, 3.6.1, 3.6.2, 3.6.3, 3.6.4; 7, §§ 1.6.1, 1.6.2, 1.6.3, 1.6.4].

Під дією прикладених сил будь-яке тверде тіло деформується, тобто змінює свої розміри та форму. Якщо після припинення дії сили тіло набуває початкових розмірів, то деформацію називають пружною (в іншому випадку – пластичною). Одне й те саме тверде тіло може внаслідок короткочасної дії сили виявити ознаки крихкості, а за досить тривалої, але слабкої дії – бути пластичним.

Пружні деформації можна спостерігати тоді, коли сила (а точніше, сила, віднесена до одиниці площі, тобто напруга), що зумовлює деформацію, не перевищує деякої, визначеної для кожного тіла межі – межі пружності. Деякі речовини (метали, каучук) можуть зазнавати значної пружної деформації, тим часом як в інших випадках (кераміка, пресовані матеріали) навіть незначна деформація перестає бути пружною.

Пластичною називається деформація, яка не зникає (принаймні цілком) після припинення дії навантаження, а отже, форма твердого тіла не відновлюється (таку деформацію називають необоротною).На пластичних деформаціях засновані технологічні процеси обробки матеріалів, об’єднані назвою «обробка металів тиском», або холодна обробка металів. До таких процесів належать прокатування (прокатне виробництво), пресування, штампування і кування (ковальсько-штампувальне виробництво) тощо.

Деформації реального тіла завжди є пластичними, але якщо величина залишкової деформації є дуже малою, нею можна знехтувати та розглядати як випадок пружної деформації.

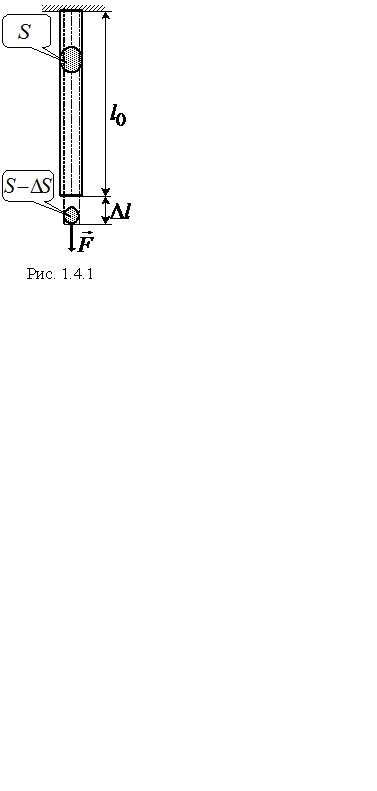Для встановлення робочої формули даної роботи розглянемо стрижень, який зазнає деформації розтягу (рис. 1.4.1). Під дією сили 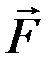стрижень з початковою довжиною l ₀ та площею поперечного перерізу S розтягується на величину абсолютного видовження .

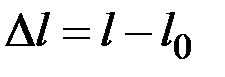Як величину, що характеризує деформацію стрижня, беруть відносну зміну її довжини Δ l / l ₀. Для стрижня із сталі відносне видовження внаслідок пружної деформації є пропорційним силі, що припадає на одиницю площі поперечного перерізу стрижня, тобто напрузі розтягу. За малих деформацій Δ l можна знехтувати зміною площі поперечного перерізу S (рис. 1.4.1). Тоді:

.

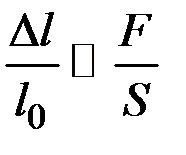Закон Гука, що виражає таку залежність, можна записати у вигляді формули:

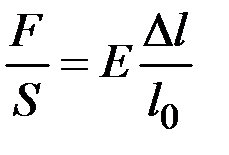, (1.4.1)

де E – модуль пружності, або модуль Юнга.

Отже, на підставі формули (1.4.1), можна записати:

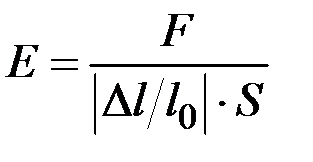. (1.4.2)

Модуль Юнга характеризує пружні властивості матеріалу і, як видно з формули (1.4.2), чисельно дорівнює силі, яку теоретично треба прикласти до стрижня, щоб збільшити його довжину вдвічі. Одиницею вимірювання модуля Юнга є 1 Н/м². Співвідношення (1.4.1) справедливе не лише для сил розтягу, а й для сил стиску.

У розглянутому випадку сила спрямована перпендикулярно до поверхні, і напруга називається нормальною. Якщо сила спрямована по дотичній до поверхні (рис. 1.4.2), на яку вона діє, напругу називають тангенціальною. Позначимо її буквою 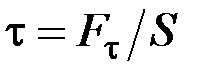, де S – площа грані, і розглянемо деформацію зсуву, що супроводжує тангенціальну напругу. Під дією напруги тіло деформується і одна грань зміщується відносно іншої на деяку відстань 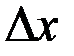. Якщо тіло уявно поділити на елементарні, паралельні до граней шари, станеться відносний зсув шарів. З цієї причини деформація такого виду називається деформацією зсуву.

Рис. 1.4.2

h

F _τ

Δ x

γ

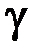Унаслідок деформації зсуву будь-яка пряма, перпендикулярна шарам, повернеться на деякий кут , тангенс якого є характеристикою деформації зсуву і називається відносним зсувом. Оскільки пружна деформація проявляється в ділянці малих зсувів, то .

Дослід свідчить, що відносний зсув є пропорційним тангенціальній напрузі, тобто: 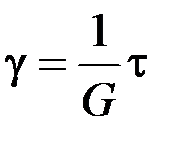, де G – коефіцієнт, який називається модулем зсуву, і, як і для модуля Юнга, його одиницею вимірювання є 1 Н/м².

Модуль Юнга і модуль зсуву повністю визначають механічні властивості однорідного твердого тіла у випадку пружних деформацій, зокрема швидкість поширення повздовжніх (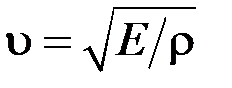) та поперечних
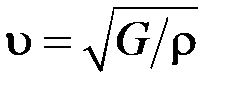() звукових хвиль, де 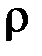– густина речовини. Унаслідок поширеня повздовжніх хвиль в середовищі відбувається періодична деформація стиску і розтягу, а за поширення поперечних – деформація зсуву.

Для визначення модуля Юнга в роботі треба знати довжину дроту, площу поперечного перерізу та виміряти видовження під дією відомої сили. Найбільше труднощів виникає під час вимірювання видовження, оскільки ця величина є дуже малою. Усі інші величини вимірюють звичайним способом: довжину – за допомогою лінійки, діаметр – за допомогою мікрометра.

Для виконання лабораторної роботи використовують установку, зображену на рис. 1.4.3. Установка складається із досліджуваного стального дроту А, верхній кінець якого нерухомо закріплено в стінному кронштейні К, а до нижнього кінця дроту прикріплено платформу С, на яку можна накладати набір каліброваних тягарців Р. Тягарці, потрібні для розтягування дроту А, беруть зі спеціального підвісу D, закріпленого на тому ж кронштейні К. Розвантажуючи дріт, тягарці слід знову розмістити на підвісі, адже саме цим досягається постійне навантаження підвісу.

Лінійка L, встановлена вертикально поблизу дроту А, використовується для вимірювання початкової довжини дроту 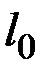від місця його вертикального закріплення до нижньої позначки B на дроті. Прецизійне вимірювання видовження дроту виконують за допомогою індикатора переміщення годинникового типу R, ціна поділки якого дорівнює 0,01 мм.

Для вимірювання видовження дроту під час його покрокового навантаження тягарцями щоразу фіксують показники індикатора годинникового типу R. Розтягальною силою, що діє з боку тягарців на дріт, є сила тяжіння, тобто F = mg, де m – сумарна маса усіх тягарців, що розтягують дріт, g = 9,81 м/с² – прискорення вільного падіння.

Нарешті, виразивши площу поперечного перерізу S через діаметр дроту d, з формули (1.4.2) отримаємо робочу формулу у вигляді:

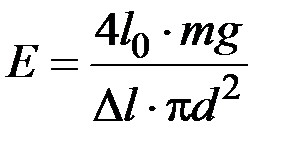, або 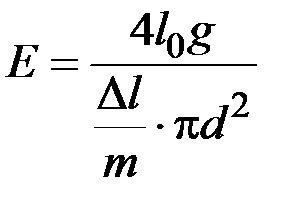. (1.4.3)

Ця формула є справедливою за умови, що деформація, якої зазнає дріт, залишається в межах її пружності.

Дата добавления: 2015-05-24