Вказівки до виконання роботи. Модуль 4. Коливальні та хвильові процеси

Лабораторна робота № 4.1. Визначення параметрів згасання коливань фізичного маятника

Модуль 4. Коливальні та хвильові процеси. Оптика

Мета роботи: вивчення основних закономірностей згасаючих коливань; визначення коефіцієнту згасання та логарифмічного декременту згасання коливань фізичного маятника.

Для виконання роботи потрібно засвоїти такий теоретичний матеріал: коливальні процеси та системи; фізичний маятник; згасаючі коливання; характеристики згасання.

Література: [ 1, т.1 §§ 10.1, 10.2, 10.4, 10.5, 10.8; 2, §§ 140–142, 146; 3, §§ 2.17, 2.18; 4, т.1 §§ 49, 50, 53, 54, 58].

Коливанням називають усякий регулярний або майже регулярний процес, в якому будь-яка величина набуває однакових значень через рівні або майже рівні проміжки часу.

Фізичний маятник − це будь-яке тверде тіло, здатне здійснювати під дією сили тяжіння коливання навколо нерухомої горизонтальної осі, яка не проходить через центр мас тіла (рис. 4.1.1).

Унаслідок відхилення фізичного маятника на деякий кут j від положення рівноваги виникає зумовлений силою тяжіння обертальний

O^/

O

j

j

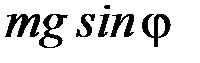
ℓ

Рис.4.1.1

момент, який прагне повернути маятник у положення рівноваги :

(4.1.1)

де m − маса тіла; ℓ − відстань від осі обертання до центра мас маятника.

Якщо маятник відпустити з такого положення, він почне здійснювати коливальний рух. Коливальному руху маятника перешкоджають опір повітря і тертя в осі маятника. Відомо, що в разі невеликої швидкості руху сумарний момент сил опору 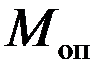буде пропорційний кутовій швидкості руху маятника:

, (4.1.2)

де – коефіцієнт опору навколишнього середовища; − кутова швидкість. Знак “мінус“ свідчить про те, що вектори та мають протилежний напрям.

За основним законом динаміки обертального руху

.

Оскільки фізичний маятник здійснює обертальний рух під дією двох моментів сил і , рівняння його руху після підстановок значень моментів сил і перетворень матиме вигляд:

, (4.1.3)

де J – момент інерції маятника відносно осі обертання; − кутове прискорення маятника.

Зважаючи на те, що за малих коливань (коливань з малими кутами відхилення, для яких можна вважати, що ), а також вводячи позначення та , диференціальне рівняння вільних згасаючих коливань фізичного маятника можна записати у вигляді:

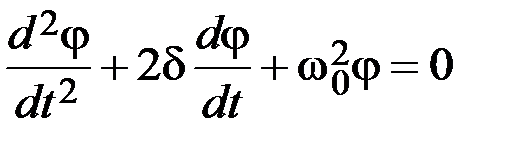. (4.1.4)

Розв’язком цього рівняння є функція залежності кута обертання маятника від часу: 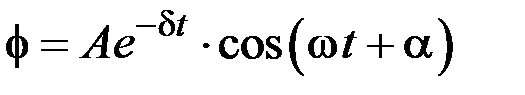. (4.1.5)

Графік функції (4.1.5) наведено на рис. 4.1.2.

Рух маятника можна розглядати як коливання з частотою та амплітудою, яка змінюється з часом за законом . Період згасаючих коливань дорівнює:

. (4.1.6)

Якщо коефіцієнт опору середовища невеликий, тобто можна вважати його рівним нулю (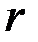 =0), то і коефіцієнт згасання d=0. Тоді формулу періоду коливань можна записати у вигляді:

. (4.1.7)

Швидкість згасаючих коливань характеризується коефіцієнтом згасання d. Для визначення коефіцієнта згасання користуються залежністю амплітуди від часу, яка подається у вигляді логарифмічної функції:

. (4.1.8)

У координатах () рівняння (4.1.8) є прямою лінією. Величина d визначає кутовий коефіцієнт нахилу прямої (4.1.8) до осі часу t (рис. 4.1.3):

або 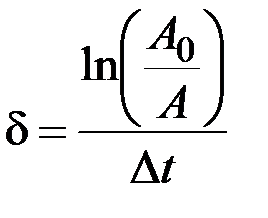. (4.1.9)

Якщо , то

.

t ₂

t ₁

t, c

d

Рис. 4.1.3

Отже, коефіцієнт згасання d – це величина, обернена до проміжку часу t_e, упродовж якого амплітуда коливань зменшується в раз. Співвідношення (4.1.9) можна використовувати для експериментального визначення d.

Окрім коефіцієнта, для характе-ристики згасання застосовують також логарифмічний декремент згасання χ, який визначають логарифмом відношення амплітуд, що відповідають моментам часу, які відрізняються на період:

. (4.1.10)

d

Рис. 4.1.4

Фізичний маятник виготовлено у вигляді металевого стрижня 1 (рис. 4.1.4), до верхнього кінця якого прикріплено дві призми, що спираються своїми ребрами на раму.

Для зміни періоду коливань на стрижень надітий масивний вантаж 2, положення якого можна регулювати гвинтами.

Відлік амплітуди коливань у градусах виконують за шкалою 3.

Дата добавления: 2015-05-24