Педагогіка як наука

S

V

V T T

VT1T2TT1T2T

№6

Закон Гей-Люсака

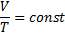
P P V

P₂ P₂ P₂<P₁

P₁ P₁ P₁

№7

Закон Дальтона

Тиск у газовій суміші дорівнює сумі парціальних тисків усіх газів у суміші.

№8

Закон Авогадро. Універсальна газова стала

При однакових тисках та температурах, об’єм 1 моля газу однаковий.

Універсальна газова стала: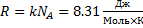

№9

Дати визначення середньої квадратичної та середньої швидкості молекул газу. Яка більша?

№10

Розподіл Максвелла. Найбільш імовірна швидкість молекул?

Якщо в системі знаходиться m частинок, то відносна кількість молекул, що матимемо в інтервалі швидкостей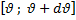

- найбільш імовірна швидкість

№11

Розподіл Больцмана. Барометрична формула

Розподіл молекул газу з висотою. Встановлюється завдяки дії сили тяжіння і теплового руху молекул.

№12

Внутрішня енергія термодинамічних систем

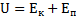
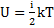(внутрішня енергія 1 частинки)

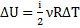(зміна внутрішньої енергії)

№13

Кількість теплоти. Зміна агрегатних станів речовини шляхом теплопередачі

Кількість теплоти – енергія, яка надається системі

– кількість теплоти при нагріванні

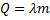– кількість теплоти при плавленні/кристалізації

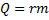– кількість теплоти при пароутворенні/конденсації

№14

Що означає, що dU є повним диференціалом? Яка основна властивість повного диференціалу

Внутрішня енергія – функція стану системи, не залежить від способу переходу з однієї точки системи в іншу, тому є повним диференціалом.

№15

Що означає твердження, що δQ та δA – варіації? Чим варіації відрізняються від повного диференціалу.

δQ та δA – варіації, бо при переході з однієї точки системи в іншу їх приріст може набувати різного значення, в залежності від способу переходу.

№16

Робота в термодинаміці. Вираз для δA при довільному процесі

Робота, яка виконується при переведенні термодинамічної системи зі стану 1 в стан 2. Дорівнює площі під графіком процесу.

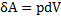
№17

Робота при ізобарному та ізохорному процесах

1)

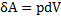
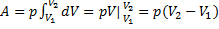
2)

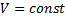
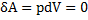
№18

Робота при ізотермічному процесі

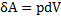
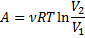
№19

Робота при адіабатичному процесі

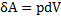
№20

1 закон термодинаміки та його застосування до різних ізопроцесів у газах

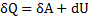
Процес	Рівняння	dU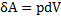
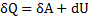
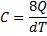
Ізохорний
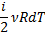
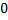
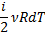
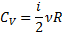
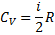
Ізобарний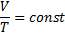
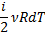
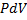
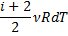
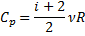
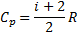
Ізотермічний
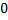
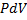
Адіабатичний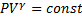

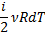
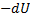
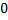
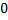
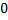
№21

Повна, питома та молярна теплоємності

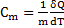- питома теплоємність

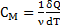– молярна теплоємність

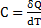- повна теплоємність

№22

Одержати вирази для молярних теплоємкостей C_p; C_ν; C_T; C_a з 1 закону термодинаміки

R

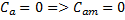
№23

Що таке ступінь вільності?

Ступінь вільності – найменше число координат, що визначає положення даної частинки в просторі

№24

Записати вирази для dU через кількість ступенів вільності та через C_ν для 1 моля і для довільної кількості газу

Процес	dU	dU(Cν)	dU(Cν 1моль)
Ізохорний V=const
Ізобарний P=const
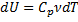
Ізотермічний T=const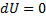
Адіабатичний Q=const

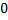
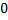
№25

Дати визначення адіабатичного процесу, рівняння адіабати.

Адіабатичний процес – це зміна стану тіла без обміну теплом з навколишнім середовищем.

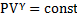- рівняння процесу

№26

Формула Майєра

C_p=C_V+R

№27

Чому дорівнює показник адіабати. Записати вираз для показника адіабати через кількість ступенів вільності?

№28

Дати визначення політропного процесу. Яким ізопроцесам відповідають записані показники політропи n=0;1;γ;∞

Політропний процес – це процес в ідеальному з довільною сталою в часі теплоємністю

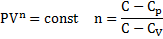
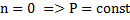- ізобарний

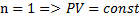– ізотермічний

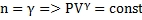– адіабатичний

- ізохорний

№29

Теплоємність при політропному процесі

№30

Записати вираз для теплоємності C_V через кількість ступенів вільності

№31

Записати вираз для C_p через кількість ступенів вільності

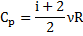
№32

Коловий процес. Оборотний та необоротний процес

Коловий процес – замкнутий цикл(прямий або зворотній).

Оборотний процес – термодинамічний процес, який здійснюється системою спочатку в прямому, а потім в зворотному напрямі, з поверненням системи в початковий стан, без змін в середовищі.

Необоротні процеси – всі інші.

№33

Чому графічно дорівнює робота при коловому процесі

Прямий цикл Зворотній цикл

P P

A>0 A<0

V₁ V₂ V V₁ V₂ V

№34

Цикл Карно в координатах P-V

P 1 ізотерма

2

4 3 адіабата

№35

Цикл Карно в координатах T-S. ККД циклу Карно

T 1(адіабата) 2

4 (адіабата) 3

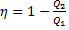, де Q₂ – теплота корисна (Або робота); Q₁ – теплота затрачена

, де T₂ – температура зовнішнього середовища; T₁ – температура нагрівача

№36

Другий закон термодинаміки

Другий закон термодинаміки – неможливо самовільно передати енергію від менш нагрітого тіла до більш нагрітого.

№37

Принцип роботи теплових машин та холодильника

Нагрівач Нагрівач

Робоче тіло Робоче тіло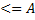

Холодильник Холодильник

№38

Дати визначення ентропії. Другий закон термодинаміки записаний через ентропію.

Ентропія (S) – міра енергії, яка не може бути використана для виконання роботи. Вона також є мірою безладдя, присутньої в системі

№39

Зміна ентропії для різних ізопроцесів у газах

Ізохора: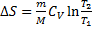

Ізотерма: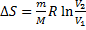

Адіабата:

№40

Нерівність Клаузіса. Об’єднання Першого та Другого законів термодинаміки.

Нерівність Клаузіса – ККД частково, або повністю необоротного циклічного процесу, завжди менша, ніж ККД оборотного циклу. Наслідок з теореми Карно.

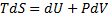– об’єднання першого та другого законів термодинаміки

№41

Третій закон термодинаміки

По мірі наближення температури до значення 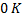, ентропія деякої рівноважної системи при ізотермічних процесах перестає залежати від будь-яких термодинамічних параметрів.

В граничному випадку ентропія приймає одне й те саме, для всіх систем, значення, яке можна приймати за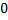

№42

Термодинамічні потенціали

Це набір функцій стану термодинамічної системи, який характеризує її поведінку при термодинамічних процесах.

1) U – внутрішня енергія

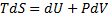
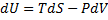
2) F – вільна енергія

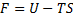
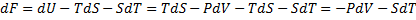
3) H – ентальпія

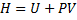
4) G – гіпсотермодинамічний потенціал

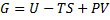
№43

Явища переносу в газах. Стаціонарні рівняння переносу

Явища переносу – це незворотні процеси в термодинамічних системах, при яких відбувається перенос енергії(теплопровідність), маси(дифузія), імпульсу(в’язкість).

	Теплопровідність	В’язкість	Дифузія
Рівняння переносу	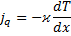Рівняння Фур’є	Рівняння Ньютона	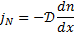Рівняння Фіка

№44

Зв'язок між коефіцієнтами переносу

Коефіцієнт теплопровідності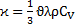

Коефіцієнт в’язкості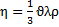

Коефіцієнт дифузії

Коефіцієнт теплопровідності зв’язується з коефіцієнтом дифузії за допомогою коефіцієнта температуропровідності

Коефіцієнт в’язкості зв’язується з коефіцієнтом дифузії за допомогою коефіцієнта кінематичної в’язкості

№45

Перелічити умови, за якими газ можна вважити ідеальним

1) Розмірами та формою частинок можна знехтувати

2) Силами взаємодії між частинками можна знехтувати

№46

Рівняння Ван-дер-Вальса. Які властивості реальних газів враховані в моделі Ван-дер-Вальса?

Фактично рівняння Ван дер Ваальса описує різницю між станом реального та ідеального газів. Також це рівняння враховує взаємодію молекул газів між собою, протягування яких зумовлене Ван-дер-Ваальсовими силами, а відштовхування принципом Паулі

№47

Ізотерми реального газу. Ізотерми Ван-дер-Вальса. Правило Максвелла.

Для дослідження поведінки реального газу розглянемо ізотерми Ван-дер-Ваальса для одного моля, які визначаються рівнянням:

.

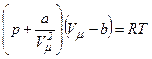Перетворимо це рівняння до вигляду:

і

.

Отримане рівняння є алгебраїчним рівнянням третього ступеня відносно молярного об’єму. Коефіцієнти рівняння залежать від тиску, температури і хімічної природи газу. Залежно від числових значень p і T для даного газу це рівняння може мати або три дійсні корені або один дійсний і два уявні, причому фізичний зміст мають лише дійсні додатні корені. Ізотерми газу, які описуються рівнянням Ван-дер-Ваальса, мають вигляд, наведений на рис. 91, де .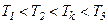

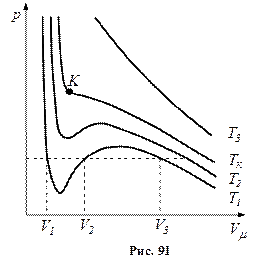При температурах 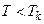є область станів, де кожному значенню тиску відповідають три точки ізотерми й ізотерма має хвилястоподібну ділянку. При підвищенні температури ці три точки зближуються і при зливаються в одну точку 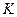, яка є точкою перегину ізотерми. Дотична до ізотерми в точці 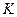паралельна до осі абсцис. При температурах ізотерми Ван-дер-Ваальса близькі до ізотерми ідеального газу.

№48

Критична точка. Критичні температура, тиск та об’єм.

При підвищенні температури серед ізотерм з хвилеподібними ділянками є одна, що не має таких ділянок. Така ізотерма називається критичною, а температура – критичною. При цій температурі зникає різниця між різними станами речовини і коефіцієнт поверхневого натягу дорівнює нулю. Відповідні об’єм 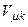і тиск 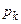називаються критичними. Стан з критичними параметрами називається критичним станом.

Знайдемо критичні параметри. Якщо

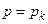, і ,

то

.

При всі три корені збігаються і дорівнюють 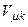. Отже, рівняння Ван-дер-Ваальса може бути записане у вигляді:

,

або

.

Отримані вище два вирази рівняння Ван-дер-Ваальса тотожні і в них повинні бути рівні коефіцієнти при однакових степенях. Тому

,
, .

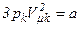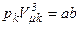Поділивши третє рівняння на друге, отримуємо вираз для 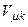. Якщо підставити отриманий вираз для 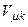у третє рівняння, маємо вираз для 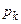. Тоді з першого рівняння, враховуючи вирази для 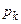і 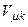, отримаємо співвідношення для . В результаті

, , .

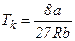Отже, критичні величини , , 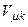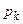безпосередньо виражаються через Ван-дер-Ваальсівські поправки a і b.

№49

Записати вирази для критичних параметрів

, , .

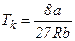№50

Фазові переходи. Зобразити лінії фазових переходів в координатах P-T

Якщо через крайні точки горизонтальних ділянок сімейства Ван-дер-Вааль­сівських ізотерм провести лінії, то одержуємо криву, що обмежує область двофазних станів речовини

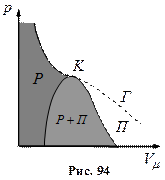Пара відрізняється від інших газоподібних станів тим, що при ізотермічному стиску відбувається процес зрідження.

Газ, який знаходиться в стані при температурі, що вища за критичну, не може бути перетворений в рідину ні при якому тиску.

Педагогіка — наука, що вивчає процеси виховання, навчання і розвитку особистості.

Назва її походить від грецьких слів «paidos» — дитина і «ago» — веду, тобто «дітоводіння». У Давній Греції так називали рабів, які супроводжували дітей рабовласників до школи, пізніше — вільнонайманих людей, котрі займалися наставництвом, вихованням та навчанням дітей. Називали ще їх педономами, дидаскалами, майстрами.

До XVII ст. педагогіка розвивалась у лоні філософії, що була тоді майже всеохоплюючою системою наукових знань. Але розвиток матеріального виробництва і духовної культури, зростання у зв'язку з цим ролі освіти і школи, розширення та ускладнення навчально-виховної діяльності й збагачення відповідного фахового досвіду зумовили виокремлення педагогіки в самостійну науку.

Кожна наука має свої предмет і об'єкт дослідження та є синтезом знань про явища дійсності, які вона вивчає. Разом з тим вона неодмінно перебуває в певних взаємозв'язках з іншими науками.

Предмет педагогіки — особлива сфера суспільної діяльності з виховання людини, складовими частинами якої є освіта і навчання.

Педагогіка досліджує виховання як свідомий і планомірний процес підготовки людини до життя і праці, розкриває його сутність, закономірності, тенденції та перспективи, вивчає принципи і правила, які регулюють виховну діяльність.

Як і кожна наука, педагогіка покликана теоретично узагальнювати факти, проникати у внутрішню природу явищ, виявляти їх причини, передбачати їх розвиток. Вона аналізує об'єктивні закономірності виховного процесу, досліджує істотні й необхідні, загальні та стійкі зв'язки, причинно-наслідкові залежності в ньому. Їх знання дає можливість правильно будувати педагогічний процес, прогнозувати результати виховання і здійснювати його відповідно до потреб суспільства.

Педагогічна наука виникла і розвивалась як теорія виховання підростаючих поколінь. Зумовлено це тим, що людина, її духовні та фізичні якості формуються в дитинстві, підлітковому віці та юності. Саме у ці періоди життя розвиток особистості відбувається найбільш інтенсивно, формуються найголовніші її риси та особливості — розумові та фізичні сили, основи світогляду, переконань, моральних почуттів, риси характеру, спрямованість потреб, інтересів, уподобань тощо. Тому істотні прогалини і недоліки у вихованні, допущені в ранньому віці, ліквідувати пізніше надзвичайно важко, а іноді й неможливо.

Педагогіка вивчає процеси виховання, освіти і навчання лише у властивих їй межах, розглядає у цих процесах тільки педагогічний аспект. Вона досліджує те, на яких загальнопедагогічних засадах, завдяки яким засобам виховної роботи потрібно будувати виховний процес, освіту і навчання людей різних вікових груп в освітніх закладах, в усіх типах установ, організацій і трудових колективів.

Дата добавления: 2015-05-24