Число. Раціональні, ірраціональні та дійсні числа

Основними поняттями сучасної математики є поняття числа, функції та границі. Хоча ці поняття мають багатовікову історію, яка іноді сягає в сиву давнину, але тільки в сучасній математиці вони набули характерної для них форми і стали наріжними каменями її будови.

Рахуючи окремі предмети, дістають так звані натуральні числа 1, 2, 3, 4,...

Вимірюючи ту чи іншу фізичну величину (час, довжину, температуру та ін.), дістають знову ж таки число. Воно може бути цілим, якщо величина, взята за одиницю масштабу, міститься у вимірюваній величині ціле число разів; дробовим, якщо існує інша менша одиниця, яка міститься ціле число разів як у вимірюваній величині, так і в обраній раніше більшій одиниці; і у цьому разі кажуть, що розглядувана величина спільномірна з одиницею міри. Нарешті, число буде ірраціональним, коли вимірювана величина неспільномірна з одиницею міри.

Розв’язання алгебраїчних задач викликало до життя у свій час (16 століття) від’ємні числа (цілі та дробові). Ще раніше (9 століття) індійці запровадили число нуль (санскритською мовою – “пустий”).

Цілі та дробові числа, як додатні, так і від’ємні разом з числом нуль звуть раціональними числами. Будь-яке раціональне число можна подати у вигляді нескоротного дробу 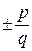, де p і q – натуральні числа. Наприклад:

; ;

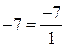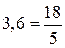
(дріб відноситься до нескоротних дробів).

Арифметичні дії над раціональними числами – додавання, віднімання, множення та ділення – завжди дають раціональне число. Ділення на нуль неприпустиме. Для практичних потреб (ліку, вимірювання, зважування та ін.) раціональних чисел цілком досить. Але в математиці та її застосуваннях обмежитись раціональними числами неможливо. Так, обчислюючи діагональ квадрата, сторона якого дорівнює 1, дістаємо число 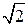, відсутнє серед раціональних чисел. Немає такого раціонального дробу (p і q – натуральні числа) квадрат якого дорівнював би 2. Справді, припустимо супротивне, а саме: що існує такий дріб , що 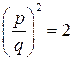. Дріб вважаємо за нескоротний (у противному разі зробили б скорочення!). З рівності 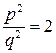маємо , тобто p є число парне . Підставляючи цю вартість p, дістанем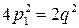о або . Звідси випливає, що й , а отже й 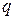- число парне. Виходить, що p і q мають спільник дільник 2, а це суперечить припущенню, що дріб - нескоротний. Отже, не існує раціонального дробу, квадрат якого дорівнює 2.

Таким чином, якщо обмежитися лише раціональними числами, то у геометрії не всім відрізкам можна було б приписати довжину, а в алгебрі просте рівняння , чи не мало б кореня. Про факт, щойно наведений з геометрії, кажуть, що діагональ квадрата неспільномірна з його стороною (довжина якої дорівнює одиниці). Можна було б навести багато фактів, які настирливо вимагали розширення поняття числа. Це розширення досягнуто запровадженням у математику (поряд з раціональними числами) ірраціональних чисел. До них належать, наприклад, числа 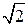, , 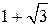, , , 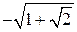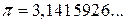та безліч інших.

З арифметики відомо що будь-яке раціональне число можна завжди виразити через скінченний десятковий дріб, або через нескінченний десятковий періодичний, або мішаний періодичний. Приміром, ; 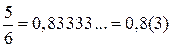. І, навпаки, будь-який періодичний десятковий дріб за відомими правилами, перетворюється у звичайний. Принципова відміна ірраціональних чисел від раціональних полягає у тому, що будь-яке ірраціональне число зображується нескінченним неперіодичним десятковим дробом.

Дата добавления: 2015-05-24