Числові ряди. Сума ряду. Умови збіжності рядів

Нехай задано числову послідовність 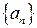. Вираз

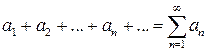(4)

називається числовим рядом. 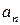- загальний елемент ряду (4), п – його номер.

Сума скінченного числа елементів ряду (4)

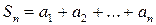(5)

називається частинною сумою ряду (4).

Ряд (4) називається збіжним, якщо 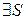, що

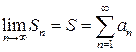(6)

У протилежному випадку ряд (4) розбігається. Число S називається сумою ряду (4).

Якщо ряд (4) збігається, тоді 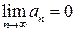(необхідна умова збіжності ряду (4)).

Приклад 1. Дослідимо на збіжність гармонічний ряд .

Необхідна умова збіжності виконується: 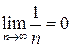. Розглянемо різницю його частинних сум, наприклад:

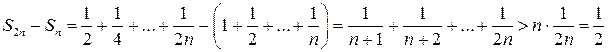Звідси випливає, що рівність 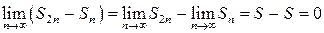неможлива, тобто гармонічний ряд розбігається.

Нехай дано два ряди 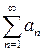і 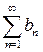з додатними елементами і 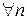виконується нерівність 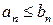. Тоді із збіжності ряду 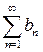випливає збіжність ряду 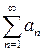, а із розбіжності ряду 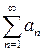–розбіжність ряду 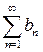(ознака порівняння).

Приклад 2. Дослідити на збіжність ряд .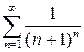

Оскільки 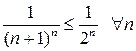і ряд 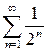збігається (як нескінченно спадна геометрична прогресія: 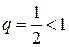), тоді, згідно з ознакою порівняння, збігається і ряд .

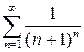Нехай задано ряд 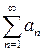з додатними елементами і 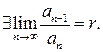Тоді: 1) за 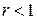ряд збігається; 2) за 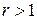ряд розбігається, 3) за 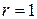ряд може як збігатися, так і розбігатися (потрібні додаткові дослідження ряду) (ознака Даламбера).

Приклад 3. дослідити на збіжність ряд .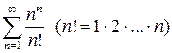

Згідно з ознакою Даламбера, маємо: 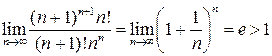(ряд розбігається).

Ряди, які містять елементи довільних знаків, називаються знакозмінними рядами.

Розглянемо ряд, побудований з абсолютних величин елементів ряду (4):

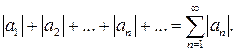(7)

Якщо ряд (7) збігається, тоді збігається і ряд (4) (достатня умова збіжності для знакозмінних рядів).

Приклад 4. Дослідити на збіжність ряд .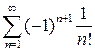

Згідно з ознакою збіжності, даний ряд збігається, оскільки збігається ряд 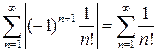. Дійсно, згідно з ознакою Даламбера, маємо: .

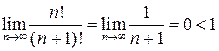Якщо 1) абсолютні величини елементів знакозмінного ряду монотонно спадають, тобто 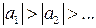і 2) 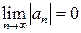, тоді такий ряд збігається (ознака Лейбніца).

Приклад 5. Дослідити на збіжність ряд .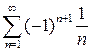

Згідно з ознакою Лейбніца, маємо: 1) 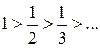і 2) .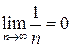

Отже, даний ряд збігається.

Зауваження. Дійсно, згідно з ознакою Лейбніца, ряд 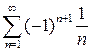збігається. У той самий час гармонічний ряд , побудований з абсолютних величин його елементів, розбігається. Ось чому усі збіжні ряди можна розділити на 1) абсолютно збіжні (одночасно збігається і сам ряд, і ряд, побудований з абсолютних величин його елементів) та 2) умовно збіжні (сам ряд збігається, а ряд, побудований з абсолютних величин його елементів, розбігається). Отже, ряд 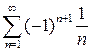– умовно збіжний, а ряд 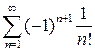– абсолютно збіжний.

Дата добавления: 2015-05-24