Визначений інтеграл. Формула Ньютона-Лейбніца. Невласні інтеграли. Ряд Фур’є

Якщо функція неперервна на , тоді вона інтегровна на ньому, тобто існує визначений інтеграл: , де числа і називаються нижньою і верхньою межею інтегрування функції відповідно. Відзначимо деякі основні властивості визначеного інтеграла, а саме:

(29)

Щоб обчислити визначений інтеграл, скористаємось основною формулою інтегрального числення (формула Ньютона-Лейбніца)

(30)

де 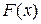– первісна функції .

Приклад 1. Обчислити інтеграл

Приклад 2. Обчислити інтеграл

Зробивши заміну в підінтегральному виразі, ми одразу змінили межі інтегрування: коли і при

Приклад 3. Обчислити площу фігури, яка обмежена графіками функцій і

Якщо фігура обмежена графіками неперервних функцій і то її площа може бути обрахована за формулою:

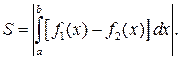(31)

Знайдемо спочатку абсциси точок перетину цих функцій, які і будуть межами інтегрування: 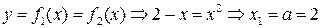і За формулою (31) маємо:

.

Приклад 4. Визначити роботу, необхідну для запуску супутника масою т з поверхні Землі вертикально вверх на висоту .

Робота змінної сили 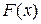по переміщенню тіла з початкової точки в кінцеву точку визначається за формулою:

(32)

Згідно із законом Ньютона, сила притягання супутника Землею визначається за формулою , де – гравітаційна стала, М – маса Землі, х – відстань від супутника до центра Землі: де – радіус Землі. За формулою (32) маємо:

Тут ми врахували той факт, що при сила притягання супутника Землею дорівнює його вазі, тобто: (прискорення вільного падіння біля поверхні Землі).

Нехай функція визначена, наприклад, на проміжку та інтегровна на будь-якому відрізку Тоді скінчену границю

(33)

називають невласним інтегралом першого роду.

Приклад 5. Обчислити інтеграл

Приклад 6. Обрахувати роботу, необхідну для виведення супутника в міжпланетний простір. Це означає, що (див. приклад 4). Отже,

Нехай функція визначена, наприклад, на проміж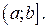ку Точку будемо називати особливою, якщо функція не обмежена в будь-якому її околі, але обмежена та інтегровна на відрізку . Тоді скінчену границю

(34)

називають невласним інтегралом другого роду.

Приклад 7. Обчислити інтеграл

Точка є особливою для підінтегральної функції. Згідно з формулою (34) маємо:

Окремо дослідимо поведінку інтеграла при :

(інтеграл розбігається).

Нехай функція визначена та інтегровна на . Тоді числа

(35)

при (п – цілі числа), (36)

(37)

називають коефіцієнтами Фур’є, а ряд

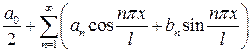(38)

називається рядом Фур’є функції .

Якщо функція парна, тоді при її інтегруванні за симетричними межами справедлива формула:

(39)

Якщо функція непарна, тоді інтеграл від неї за симетричними межами тотожно дорівнює нулю.

Зауваження. Якщо функція парна, тоді коефіцієнти , а якщо непарна, тоді коефіцієнти .

Приклад 8. Розкласти в ряд Фур’є на функцію . Оскільки функція є парною тоді і

Отже, шуканий ряд Фур’є функції має такий вигляд:

Дата добавления: 2015-05-24