Основные законы аэродинамики. Уравнение неразрывности

Уравнение неразрывности.

Уравнение неразрывности струи воздушного потока (постоянства расхода) - это уравнение аэродинамики, вытекающее из основных законов физики - сохранения массы и инерции. Устанавливает связь между плотностью, скоростью и площадью поперечного сечения струи воздушного потока.

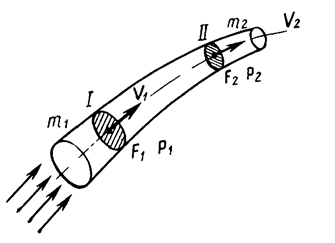
Рис. 2.5 Пояснение к закону неразрывности струи воздушного потока

Уравнение сформулировано Л. Эйлером в 1756г. применительно к движению струйки жидкости.

В струйке переменного сечения через сечение I за одну секунду протекает некоторый объем воздуха (рис.2.5). Этот объем равен произведению скорости воздушного потока V на площадь поперечного сечения F.

Секундный массовый расход воздуха в струйке m_c равен произведению секундного объема на плотность ρ воздушного потока.

Согласно закону сохранения материи масса жидкости (воздуха) в струйке m₁, протекающей через сечение I, должна быть равна массе m₁, протекающей через сечение II, при условии, если движение воздушного потока установившееся:

m₁=m₂=cons, ρ₁ F₁V₁₌ ρ₂ F₂V₂=const.

Для любого сечения струйки можно записать:

ρFV=const.

Это выражение называется уравнением неразрывности ( постоянства расхода ) для струйки воздушного потока.

При малых скоростях движения воздух ведет себя как несжимаемая жидкость. Поэтому плотность воздуха в любом сечении струйки одинакова r₁=r₂=const.

Для несжимаемой жидкости уравнение можно записать в следующем виде : F₁V₁=F₂V₂= const или в виде пропорции:

Из формулы видно, что для любого сечения скорость воздушного потока струи обратно пропорциональна площади ее поперечного сечения и наоборот:

V =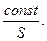

Вывод: Уравнение неразрывности устанавливает взаимосвязь между сечением струи и скоростью при условии, что воздушный поток струи установившийся.

Задача. Определить скорость течения потока жидкости V₂ в узком сечении трубки площадью S₂=5см²,если через широкое сечение трубки площадью S₁=7,5см² скорость течения составляет V₁=20м/с.

Решение: V₂/V₁=S₁/S₂. V₂=V₁S₁/S₂=20*7,5/5=30м/с.

Дата добавления: 2015-05-08