Контрольная работа № I 1 страница

Общие методические указания

Контрольные задания

Согласно учебному плану студент-заочник выполняет две контрольные работы, каждая из которых состоит их четырех задач по различным разделам курса.

Контрольные задачи составлены по стовариантной системе, в которой исходные данные к каждой задаче выбираются из таблиц по последней и предпоследней цифрам шифра студента-заочника. Работы, выполненные по чужому варианту, не рецензируются.

При решении контрольных задач необходимо придерживаться следующих правил:

а) выписывать условие задачи и исходные данные;

б) решение сопровождать краткими пояснениями;

в) вычисления выполнять в международной системе единиц СИ;

г) в конце работы привести список использованной литературы и поставить свою подпись;

д) для письменных замечаний рецензента на каждой странице оставить чистые поля и одну–две страницы в конце работы;

е) на обложке тетради указать номер контрольной работы, название предмета, фамилию, имя, отчество, свой шифр и номер специальности.

Задача 6.1. Воздух, имеющий начальное давление P ₁=0,1МПа и температуру t ₁=20°C, сжимается в одноступенчатом поршневом компрессоре до давления Р ₂. Сжатие может быть изотермическим, адиабатным и политропным с показателем политропы n. Определить для каждого процесса сжатия все начальные и конечные параметры воздуха, считая его идеальным газом; отведенную от воздуха теплоту Q, кВт и теоретическую мощность привода компрессора N, кВт, если производительность компрессора G, кг/с. Дать сводную таблицу и изображение процессов сжатия в pv- и Ts -диаграммах. Исходные данные выбрать из табл. 6.1.

Таблица 6.1.

Исходные данные к задаче 6.1.

Последняя цифра шифра	n	Предпоследняя цифра шифра	P2, МПа	G, кг/с
	1,10 1,12 1,14 1,16 1,18 1,20 1,22 1,24 1,26 1,28		0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7	0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0

РЕШЕНИЕ (вариант 99). Для воздуха, как для идеального газа, принять: изохорную массовую теплоемкость C _v=0,72кДж/кг×К, газовую постоянную R =287Дж/кг×К, показатель адиабаты К=1,41. тогда начальный удельный объем воздуха по уравнению Клапейрона:

.

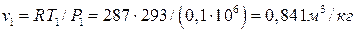Конечные температуры воздуха при изотермическом, адиабатном и политропном сжатиях соответственно:

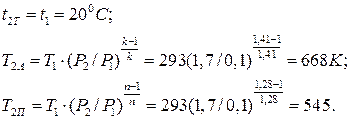
Конечные удельные объемы воздуха по уравнению Клапейрона:

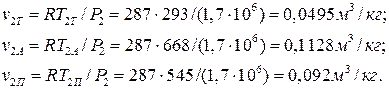
Теплота, отведенная от воздуха, по уравнению теплового баланса:

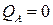(процесс без теплообмена)

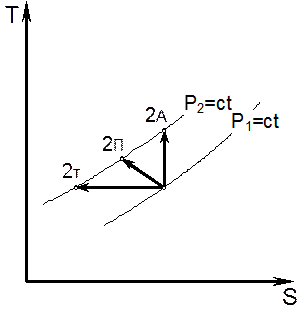Рис. 6.2. TS-диаграмма процессов сжатия.

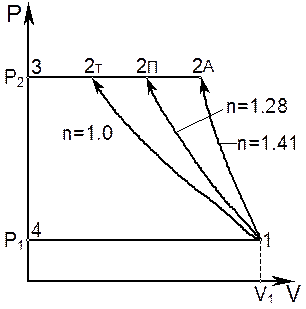Рис. 6.1. Pv-диаграмма процессов сжатия.

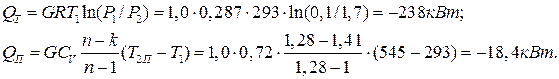
где знак (–) означает, что тепло отводится от сжимаемого воздуха.

Теоретические мощности привода компрессора:

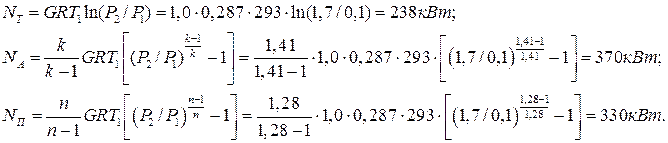
что подтверждает вывод о том, что мощность привода изотермического компрессора минимальна, а адиабатного – максимальна.

Таблица 6.2

Сводная таблица рассчитанных величин

Величина	Изотермическое сжатие	Адиабатное сжатие	Политропное сжатие
T2, К V2, м^3/кг Q, кВт N, кВт	0,0495 -238	0,1128	0,092 -18,4

Задача 6.2. Рассчитать теоретический цикл двигателя внутреннего сгорания (ДВС), считая, что рабочим тело является воздух с начальными параметрами P_{1 ­} =0,1МПа, t₁ =20°С. Определить основные параметры рабочего тела P, V, T во всех точках цикла, изменение внутренней энергии D U, энтальпии D h, энтропииD S для всех процессов и для цикла; теплоту и работу для процессов и для цикла, а также термический КПД цикла. Дать сводную таблицу и изобразить цикл в PV - и TS -диаграммах. Исходные данные брать из табл. 6.3.

Таблица 6.3

Исходные данные к задаче 6.2

Последняя цифра шифра	Цикл	Степень сжатия, e	Предпо-следняя цифра шифра	Степень повыше-ния давления, l	Степень предвари-тельного расши-рения, r
	Отто *)   Дизеля **)     Тринклера-Сабатэ			2,4 2,3 2,2   2,1 2,0 1,9   1,8 1,7 1,6 1,5	2,1 2,0 1,9   1,8 1,7 1,6   1,5 1,4 1,3 1,2

Примечание: независимо от исходных данных принимать *) r=1 для циклов с изохорным подводом теплоты (цикл Отто) и **) l=1 для циклов с изобарным подводом теплоты (цикл Дизеля).

РЕШЕНИЕ (вариант 99). Для воздуха, как для идеального газа, принять: теплоемкости C_p =1,01кДж/(кгК) и C_v =0,72 кДж/(кгК); газовую постоянную R =287 Дж/(кгК), показатель адиабаты K =1,41. Для варианта 99 задан цикл ДВС со смешанным подводом теплоты (цикл Тринклера-Сабатэ).

Начальный удельный объем рабочего тела по уравнению Клапейрона:

.

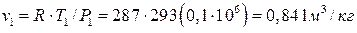По степени сжатия e= v₁/v₂ находим удельный объем рабочего тела в точке 2

.

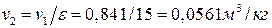Процесс 1-2 – это адиабатное сжатие рабочего тела, а уравнение адиабатного процесса

,

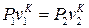Откуда находится давление в точке 2:

.

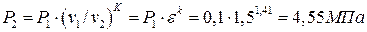Температура в точке 2 находится по уравнению Клапейрона:

.

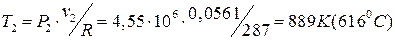Для изохорного процесса подвода тепла к рабочему телу 2-3 характеристикой является степень повышения давления l= P₃/P₂, откуда находится давление в точке 3:

.

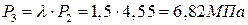С учетом того, что для изохорного процесса v₃= v₂ =0,0561м³/кг, температура рабочего тела в точке 3 по уравнению Клапейрона:

.

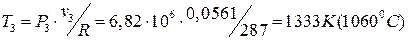Для изобарного процесса подвода тепла к рабочему телу 3-4 характеристикой является степень предварительного расширения r= V₄/V₃, откуда находится удельный объем рабочего тела в точке 4:

.

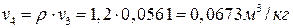Для изобарного процесса P₄=P₃= 6.82МПа, тогда температура рабочего тела в точке 4 по уравнению Клапейрона:

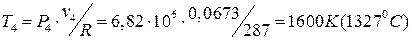
С учетом того, что процесс 5-I – это изохорный отвод тепла от рабочего тела, 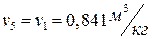. Тогда для адиабатного процесса расширения рабочего тела 4-5: 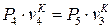, откуда находится давление в точке 5:

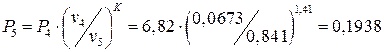МПа.

Температура рабочего тела в точке 5 по уравнению Клапейрона:

.

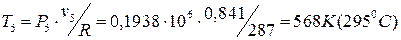Параметры всех точек цикла сводим в табл. 6.4.

Таблица 6.4

Рассчитанные параметры точек цикла

Параметры	Точки
Давление Р, МПа	0,1	4,55	6,82	6,82	0,1938
Удельный объем n, м^3/кг	0,841	0,0561	0,0561	0,0673	0,841
Температура Т, К
Температура t, ºC

Изменение внутренней энергии в процессах и для цикла в целом:

∆ ;

∆ ;

∆ ;

∆ ;

∆ ;

∆ .

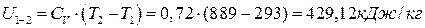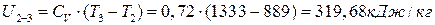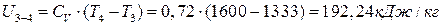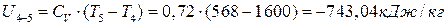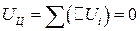Суммарное изменение внутренней энергии в цикле ∆ 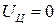, что подтверждает правильность расчетов, так как

∆ .

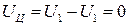Изменение энтальпии в процессах и для цикла в целом:

∆ ;

∆ ;

∆ ;

∆ ;

∆ ;

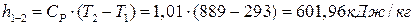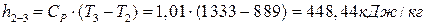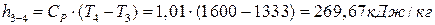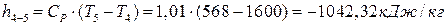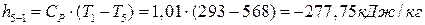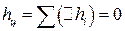∆ , действительно: ∆ .

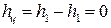Изменение энтропии в процессах и для цикла в целом: 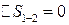, так как это процесс адиабатный, то есть без теплообмена между рабочим телом и окружающей средой:

;

;

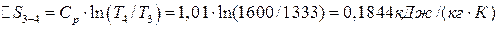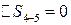, так как это процесс адиабатный;

;

,

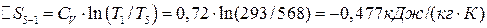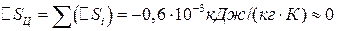что также подтверждает правильность расчетов, так как

.

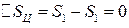Работа процессов и цикла в целом

,

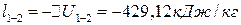так как это процесс адиабатный, то есть без отвода теплоты от рабочего тела, поэтому внутренняя энергия рабочего тела возрастает за счет теплоты сжатия, а знак “-” означает затрату работы на сжатие газа.

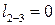, так как в изохорном процессе нет измерения объема газа, следовательно, работа против внешних сил не совершается.

;

; .

.

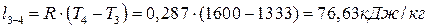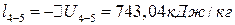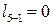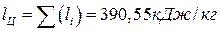Теплота процессов и цикла в целом; 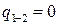, так как это процесс адиабатный, то есть без теплообмена;

;

;

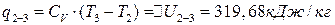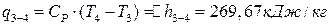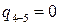, так как это адиабатный процесс;

,

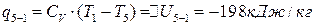
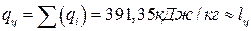что подтверждает правильность расчетов, так как для циклов 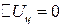, следовательно, по I закону термодинамики .

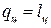Термический КПД цикла представляет собой отношение работы цикла к подведенной к рабочему телу теплоте:

.

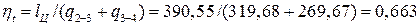Проверка:

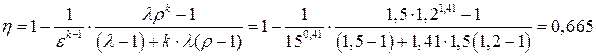
Погрешность расчета:

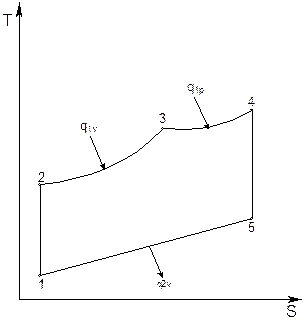Рис. 6.4. TS-диаграмма цикла Тринклера-Сабатэ.

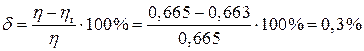<1%, то есть точность расчета достаточная.

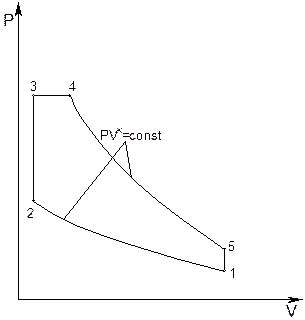Рис. 6.3. Pv-диаграмма цикла Тринклера-Сабатэ.

ЗАДАЧА 6.3. Определить эффективную мощность Ne газотурбинной установки (ГТУ) без регенерации теплоты и ее эффективный КПД по заданной степени повышения давления 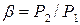, известным адиабатным КПД турбины 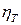и компрессора 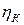, температуре воздуха перед компрессором 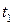, температуре газа перед турбиной 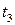и по расходу воздуха через ГТУ 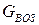. Изобразить цикл ГТУ в PV- и TS- диаграммах. Показать, как зависит термический КПД ГТУ от степени повышения давления 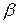. Исходные данные выбрать из табл.6.5.

Таблица 6.5

Исходные данные к задаче 6.3

Послед-няя цифра шифра	t1,ºC	t3, ºC	β	Предпос-ледняя цифра шифра	ηк	ηТ	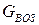, кг/с
			7,2 9,0 8,8 8,5 8,2 8,0 7,5 7,0 6,5 6,2		0,82 0,81 0,79 0,82 0,81 0,80 0,79 0,78 0,77 0,76	0,89 0,88 0,85 0,87 0,86 0,84 0,82 0,86 0,83 0,85

РЕШЕНИЕ (вариант 99). В расчете принимать теплоемкость воздуха и газа С_р=1,01кДж/(кгК); показатель адиабаты К=1,41; механический КПД ГТУ η_м=0,98; давление воздуха перед компрессором Р₁=0,1 МПа.

Удельный объем воздуха перед компрессором по уравнению Клапейрона:

.

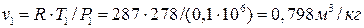Температура воздуха после компрессора при адиабатном теоретическом сжатии по уравнению адиабатного процесса:

;

,

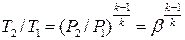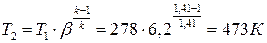а при действительном адиабатном сжатии – из выражения внутреннего адиабатного КПД компрессора:

;

.

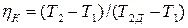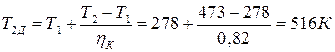Давление сжатого воздуха в компрессоре

.

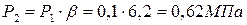Удельные объемы воздуха в точках 2, 2Д, 3 по уравнению Клапейрона:

;

;

.

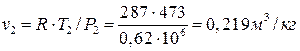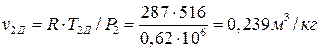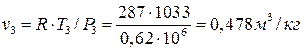Температура газов после газовой турбины при адиабатном теоретическом расширении

;

,

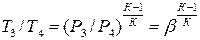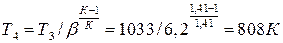а при действительном адиабатном расширении – из выражения внутреннего адиабатного КПД газовой турбины

;

.

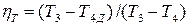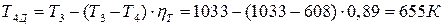Удельные объемы газа в точках 4 и 4Д по уравнению Клапейрона:

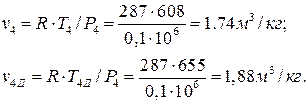
Для построения цикла ГТУ в TS – диаграмме необходимо определить изменения энтропии в процессах:

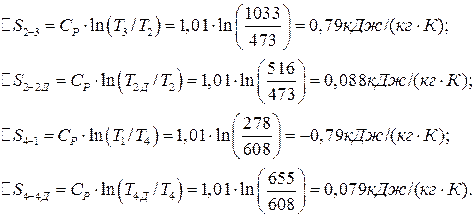
Эффективная работа ГТУ:

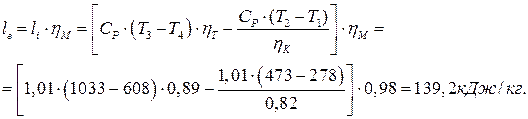
Эффективный КПД ГТУ:

.

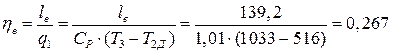Эффективная мощность ГТУ:

.

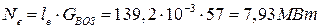Зависимость термического КПД цикла ГТУ от степени повышения давления определялась по выражению

,

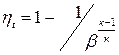результаты расчетов по которому представлены в табл.6.6.

Таблица 6.6

Зависимость термического КПД цикла

без регенерации теплоты от степени повышения

давления

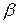
		6,2
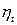
	0,374	0,412	0,432	0,454	0,472

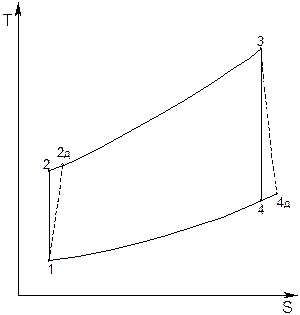Рис. 6.6. TS-диаграмма ГТУ без регенерации теплоты.

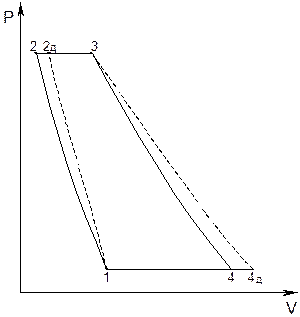Рис. 6.5. Pv-диаграмма ГТУ без регенерации теплоты.

Из табл. 6.6 следует, что термический КПД возрастает с увеличением степени повышения давления в компрессоре.

ЗАДАЧА 6.4. Определить термический КПД цикла Ренкина и эффективную мощность паротурбинной установки (ПТУ) по заданным начальному давлению Р₁ и температуре перегретого пара перед турбиной t₁; конечному давлению в конденсаторе Р₂, расходу пара через турбину D, внутренним относительным КПД турбины η_Т и питательного насоса η_Н. Изобразить цикл Ренкина в TS – диаграмме, а процессы сжатия воды в питательном насосе и расширения пара в турбине – в hS – диаграмме. Механический КПД ПТУ принять равным η_М=0,98. Исходные данные выбрать из табл.6.7.

Таблица 6.7

Исходные данные к задаче 6.4

Послед-няя циф-ра шифра	Р1, МПа	t1, ºC	ηТ	Предпос-ледняя цифра шифра	Р2, кПа	D, кг/с	ηН
	10,0		0,80		3,0		0,70
	10,5		0,81		3,5		0,71
	11,0		0,82		4,0		0,72
	11,5		0,83		4,5		0,73
	12,0		0,84		5,0		0,74
	12,5		0,85		3,0		0,75
	13,0		0,86		3,5		0,76
	13,5		0,87		4,0		0,77
	14,0		0,88		4,5		0,78
	14,5		0,89		5,0		0,79

РЕШЕНИЕ (вариант 99). Решение может быть выполнено с помощью hS – диаграммы водяного пара (приближенное) или с помощью таблиц термодинамических свойств воды и водяного пара (точное).

На рис. 6.7…6.9 изображены процессы в паротурбинной установке: 1-2 – теоретическое адиабатное расширение пара в турбине; 1-2_Д – действительное расширение пара; 2- 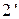– изобарно-изотермическая конденсация пара в конденсаторе; 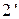-3 – теоретическое адиабатное сжатие воды в питательном насосе; 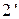-3_Д – действительное сжатие воды (в TS – диаграмме эти процессы не отражены, ввиду малого изменения параметров воды в этих процессах; они изображены в увеличенном масштабе в hS – диаграмме на рис. 6.8); 3_Д-4 – изобарный нагрев воды до температуры насыщения в водяном экономайзере; 4-5 – изобарно-изотермическое парообразование в парогенераторе; 5-1 – изобарный перегрев пара в пароперегревателе.

Точка I в hS –диаграмме находится на пересечении изобары Р₁ = 145 бар и изотермы t₁ = 590º C, для которой находится энтальпия перегретого пара перед турбиной h₁ = 3586 кДж/кг. Теоретическое расширение пара в турбине 1-2 изображается вертикальной линией S₂ = S₁ до пересечения с изобарой Р₂ = 0,05 бар, откуда в точке 2 находится энтальпия пара после турбины h₂ = 2035 кДж/кг.

Ниже приведены таблицы 6.8 и 6.9 термодинамических свойств воды и водяного пара, с помощью которых задача решается более точно. Критические параметры воды: Р_кр = 221,29 бар; t_кр = 374,15 º C; v_кр = 0,00326 м³/кг; h_кр = 2100 кДж/кг; S_кр = 4,43 кДж/(кгК).

Из табл. 6.9 свойств перегретого пара для давления Р₁ = 145 бар и температуры t₁ = 590º C находим методом линейной интерполяции энтальпию h₁ = 3554 кДж/кг и энтропию перегретого пара перед турбиной S₁ = 6,67 кДж/(кгК).

Теоретическое адиабатное расширение пара происходит при постоянной энтропии S₂ = S₁ = 6,67 кДж/(кгК) до давления Р₂ = 0,05 бар. Из hS – диаграммы процесса на рис. 6.9 видно, что состояние пара после турбины (в точке 2) соответствует влажному насыщенному пару, для которого энтропия находится по формуле:

,

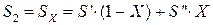где энтропия воды на линии насыщения при давлении Р₂ = 0,05 бар по табл. 6.8 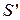= 0,4761 кДж/(кгК) и энтропия сухого насыщенного пара 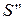= 8,393 кДж/(кгК). Тогда степень сухости влажного пара после турбины (в точке 2):

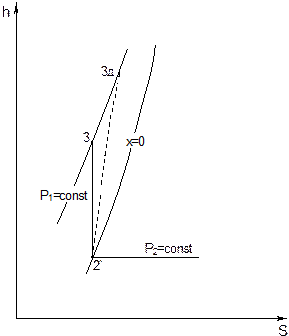Рис. 6.8. Процессы теоретического 2´-3 и действительного 2´-3_Д сжатия воды в питательном насосе.

.

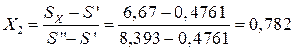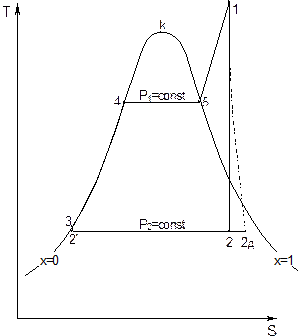Рис. 6.7. Цикл Ренкина в TS-диаграмме.

Рис. 6.9. Процессы расширения пара в турбине: 1-2- - теоретический; 1-2_Д – действительный.

Таблица 6.8

Таблица термодинамических свойств сухого насыщенного пара

и воды на линии насыщения

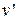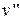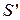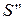РН, бар	tH, º C	, м^3/кг	, м^3/кг	, кДж/кг	, кДж/кг	r, кДж/кг	, кДж/(кгК)	, кДж/(кгК)
0,010	6,92	0,001000	129,9	29,3			0,1054	8,975
0,025	21,09	0,001002	54,24	88,5			0,3124	8,642
0,050	32,88	0,001005	28,19	137,8			0,4761	8,393
0,075	40,32	0,001008	19,23	168,8			0,5764	8,250
0,100	45,84	0,001010	14,68	191,9			0,6492	8,149
1,00	99,64	0,001043	1,694	417,4			1,3026	7,360
10,0	179,88	0,001127	0,1946	762,7			2,138	6,587
	263,91	0,001286	0,0394				2,921	5,973
	303,32	0,001417	0,0205				3,287	5,678
	310,96	0,001452	0,0180				3,360	5,615
	318,04	0,001489	0,0160				3,430	5,553
	324,63	0,001527	0,0143				3,496	5,492
	330,81	0,001567	0,0128				3,561	5,432
	336,63	0,001611	0,0115				3,623	5,372
	342,11	0,001658	0,0104				3,684	5,310
	347,32	0,001710	0,0093				3,746	5,247

Дата добавления: 2015-05-08