Теоретические основы электротехники 1 страница

1.1. Основные понятия и законы теории электрических цепей

Электрическая цепь - это совокупность устройств, образующих путь для электрического тока, электромагнитные процессы в которых могут быть описаны с помощью понятий об электродвижущей силе, токе и напряжении. Все составные части электрической цепи во время ее работы охвачены единым электромагнитным процессом, характеризующимся сложной совокупностью физических явлений. Поэтому процессы в электрических цепях определенным образом идеализируются, а реальные объекты электрической цепи заменяются элементами, удобными для математического описания. Таким образом, любой электрической цепи может быть поставлена в соответствие идеализированная схема замещения. Далее, говоря об электрической цепи (схеме), будем иметь в виду, что речь идет о введенной таким образом схеме замещения.

1.1.1. Элементы электрических цепей

Пассивными элементами (параметрами) электрической цепи являются сопротивление r, индуктивность L и емкость С. Условные графические обозначения элементов приведены на рис. 1.1. В реальных цепях сопротивлением, индуктивностью и емкостью обладают соответственно резисторы, катушки и конденсаторы.

r L C

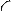
Рис. 1.1

Сопротивление - это идеализированный элемент цепи, в котором происходит необратимое преобразование электрической энергии в тепловую. Сопротивление определяется как отношение напряжения на зажимах элемента к току, который через него протекает

r = u/i,

где r - сопротивление, Ом.

Индуктивность - это идеализированный элемент цепи, характеризующийся способностью накапливать энергию магнитного поля.

Если по катушке с числом витков w протекает ток i, вызывающий магнитный поток Ф, то индуктивность L - это коэффициент, связывающий потокосцепление Y = wФ с током:

где L - индуктивность, Гн (генри).

Емкость - это идеализированный элемент, характеризующийся способностью накапливать энергию электрического поля. Емкость выступает коэффициентом между зарядом на обкладках конденсатора и приложенным к нему напряжением:

q = C×u,

где С - емкость, Ф (фарада).

Для работы электрической цепи необходимо наличие в ней активных элементов, т. е. источников электрической энергии. В любом источнике электрической энергии за счет сторонних (некулоновских) сил создается электродвижущая сила. При этом на зажимах источника возникает напряжение, под действием которого во внешней части цепи протекает ток. Источник электрической энергии может работать в режиме источника ЭДС или в режиме источника тока.

Источник ЭДС - это идеализированный источник электрической энергии, внутреннее сопротивление которого равно нулю. Условное графическое обозначение источника ЭДС приведено на рис. 1.2а. Источник ЭДС характеризуется тем, что напряжение на его зажимах не зависит от величины тока нагрузки.

Е

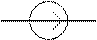а) б)

Рис. 1.2

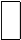
Реальные источники электрической энергии обладают внутренним сопротивлением. Схема реального источника напряжения и его вольт - амперная (внешняя) характеристика приведены на рис. 1.3.

а Uав

rвн = 0

rвн I rн E

rвн ¹ 0

U_ab

E

в I

а) б)

Рис. 1.3

Уравнение внешней характеристики реального источника напряжения имеет вид

, (1.1)

т. е. напряжение на зажимах источника меньше его ЭДС на величину падения напряжения на внутреннем сопротивлении.

Источник тока - это идеализированный источник электрической энергии, внутреннее сопротивление которого бесконечно велико. Обозначение источника тока приведено на рис. 1.2б. Ток идеального источника тока не зависит от величины сопротивления внешней части цепи. Схема реального источника тока и его внешняя характеристика приведены на рис. 1.4.

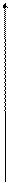а I Uав r ¹ 0 r = 0

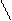
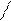
Iвн Uав

r

rвн

в

I

а) б)

Рис. 1.4

Учитывая, что

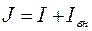и ,

получим выражение внешней характеристики реального источника тока:

. (1.2)

Сравнивая выражения (1.1) и (1.2), можно сделать вывод, что реальный источник электрической энергии может быть представлен как схемой реального источника напряжения (рис. 1.3а), так и схемой реального источника тока (рис. 1.4а). Эквивалентный переход от одной схемы к другой осуществляется через соотношение

.

Различают линейные и нелинейные элементы схемы замещения электрической цепи. Линейными называют элементы, параметры которых (r, L, C) не зависят от тока или напряжения, действующего на этих элементах. Такие элементы имеют линейные вольт-амперные характеристики. Кроме того, для линейных цепей выполняется принцип наложения: ток в любом из элементов такой цепи от действия нескольких источников электрической энергии может быть найден как алгебраическая сумма токов от действия каждого из источников в отдельности.

1.1.2. Ток и напряжение в элементах электрической цепи

При расчете цепи необходимо указать на схеме положительные направления токов, напряжений и ЭДС. Положительным направлением ЭДС считают направление, в котором внутри источника перемещаются положительные заряды, т. е. стрелки в источнике ЭДС и источнике тока направлены в сторону большего потенциала. Положительным направлением тока считают направление движения положительных зарядов, т. е. ток течет от большего потенциала к меньшему. Положительное направление напряжения на элементах цепи совпадает с положительным направлением тока.

Мгновенные значения тока, напряжения и ЭДС принято обозначать строчными буквами (i, u, e), не зависящие от времени - прописными (I, U, E). Перед расчетом цепи условные положительные направления токов задают произвольно. Если полученное в результате расчета значение тока положительно, значит действительное направление тока совпадает с заданным.

Для составления уравнений, описывающих электромагнитные процессы в цепи, необходимо знать связь между током и напряжением на элементах электрической цепи. Связь между током и напряжением на сопротивлении определяется законом Ома

.

Отсюда следует, что форма тока через сопротивление повторяет форму напряжения. Связь между током и напряжением на индуктивности устанавливается на основе закона электромагнитной индукции:

.

Учитывая, что на основе закона Ленца

, ,

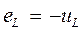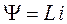получим

и .

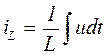Таким образом, напряжение на индуктивности определяется скоростью изменения тока.

Временные диаграммы (рис. 1.5) иллюстрируют связь между током и напряжением на индуктивности.

Ток через конденсатор равен скорости изменения заряда на его обладках:

.

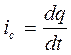Учитывая, что , получим связь между током и напряжением на емкости:

, .

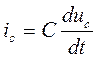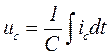Tаким образом, ток через емкость определяется скоростью изменения напряжения (рис. 1.6).

1.1.3. Мгновенные мощность и энергия

Пусть электрическая цепь, представленная в виде пассивного двухполюсника, подключена к источнику (рис. 1.7). Энергия источника затрачивается на работу по перемещению зарядов в направлении тока i. Если за время dt через двухполюсник переносится заряд dq, то совершаемая при этом элементарная работа или, что то же самое, поступающая в цепь элементарная энергия

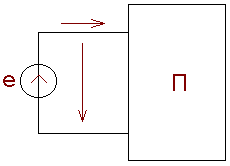
Рис. 1.7

Отсюда энергия, затраченная на перемещение заряда от момента времени t = -¥, где энергия принимается равной нулю, до рассматриваемого момента времени t

.

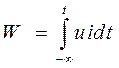Энергия измеряется в джоулях (Дж).

Мгновенная мощность - это скорость изменения энергии:

.

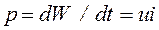Таким образом, мгновенная мощность равна произведению мгновенных значений напряжения и тока. Знак мгновенной мощности указывавет направление передачи энергии: если р > 0, то цепь (или элемент цепи) потребляет энергию, если р < 0 - отдает энергию. Мощность измеряется в ваттах (Bт).

Мгновенная мощность в сопротивлении

всегда положительна, т. е. энергия всегда поступает от источника в элемент и необратимо преобразуется в тепло.

Мощность в индуктивности

,

т. е. индуктивность накапливает энергию, если i > 0 и ток через индуктивность нарастает.

Полагая, что при t = -¥ i = 0, а в момент t ток равен i, получим выражение энергии, запасенной в индуктивности:

,

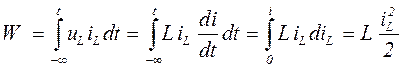т. е. энергия в индуктивности пропорциональна квадрату тока.

Мощность в емкости:

,

т. е. емкость накапливает энергию, если uc > 0 и напряжение на емкости нарастает.

Энергия, накапливаемая в емкости:

.

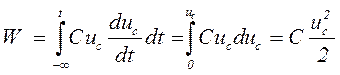1.1.4. Законы Кирхгофа

В основе расчета электрических цепей лежат законы Кирхгофа. Введем некоторые понятия, которые содержатся в формулировках этих законов. Участок цепи, по всем элементам которого проходит один и тот же ток, называют ветвью. Место соединения трех и более ветвей называют узлом. Любой замкнутый путь, включающий несколько ветвей, называют контуром.

Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю:

.

Если ток в k-й ветви направлен к узлу, то его берут со знаком “плюс”, в противном случае - со знаком “минус”.

Второй закон Кирхгофа: в любом контуре алгебраическая сумма падений напряжения равна алгебраической сумме ЭДС:

.

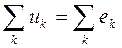Если в k-м контуре направления падений напряжения и ЭДС совпадают с произвольно выбранным направлением обхода контура, то их берут со знаком “плюс”, в противном случае - со знаком “минус”.

Пусть цепь содержит q узлов и p ветвей. Тогда для расчета всех токов необходимо составить q - 1 уравнение по первому закону Кирхгофа и p-(q-1) уравнение - по второму закону Кирхгофа. Уравнения по второму закону Кирхгофа составляют для независимых контуров (каждый из которых отличается от других хотя бы одной новой ветвью), не содержащих источников тока.

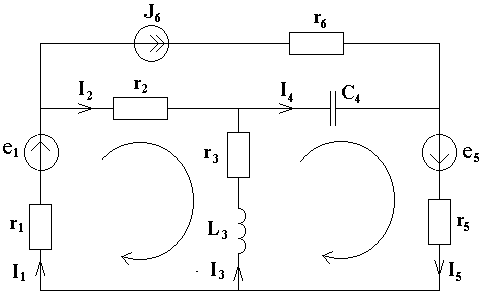
Рис. 1.8

Например, для схемы (рис. 1.8.) уравнения, составленные по законам Кирхгофа имеют вид

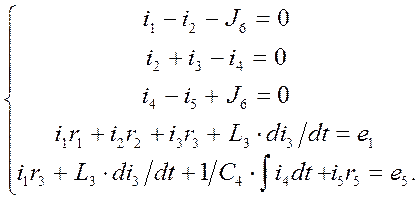
1.2. Цепи синусоидального тока

В электроэнергетике получение, преобразование и потребление электроэнергии осуществляется в основном на синусоидальном токе. Это связано с возможностью преобразования напряжения переменного тока с помощью трансформатора - относительно простого устройства, имеющего высокий КПД. Высокое напряжение используют для экономичной передачи электроэнергии на большие расстояния, пониженное - для питания потребителей.

1.2.1. Синусоидальный ток и его основные характеристики

Синусоидальным называют периодический ток, являющийся синусо-идальной функцией времени (рис. 1.9):

:

Рис. 1.9

Синусоидальный ток характеризуется тремя параметрами:

- амплитудой Im - максимальное значение тока;

- периодом Т - наименьший интервал времени, по истечении которого мгновенные значения тока повторяются;

- начальной фазой a - определяет значение тока в момент времени t=0.

Аргумент синусоидального тока 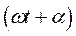называют фазой. Скорость изменения фазы называют угловой частотой:

.

Величину, обратную периоду называют частотой:

f = 1/T.

Величиной, характеризующей энергетическое действие тока, является его действующее значение. Действующее значение переменного тока численно равно такому значению постоянного тока, который выделяет в некотором сопротивлении одинаковое с переменным током количество энергии.

Пусть постоянный ток I за время Т выделяет в сопротивлении r энергию

, (1.3)

а переменный ток i

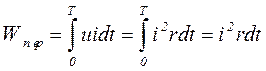. (1.4)

Приравнивая (1.3) и (1.4), получим

,

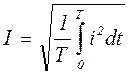т. е. математически действующее значение переменного тока - это его среднее квадратичное за период.

Найдем действующее значение синусоидального тока :

.

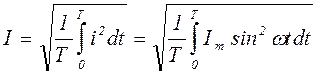Подкоренное выражение

.

Итак, действующее значение синусоидального тока

.

Аналогично определяются действующие значения синусоидального напряжения и ЭДС:

, .

Если речь идет о периодических напряжениях и токах, обычно подразумевают их действующие значения.

1.2.2. Изображение синусоидальных токов, напряжений и ЭДС

при помощи векторных диаграмм.

При расчете электрических цепей приходится складывать, вычитать, качественно сопоставлять величины токов и напряжений, являющихся синусоидальными функциями времени. Решение таких задач с использованием тригонометрических преобразований оказывается громоздким. Задача упрощается, если оперировать не синусоидальными функциями времени, а отрезками, проекции которых на некоторую ось образуют данные синусоидальные функции. Пусть отрезок длиной (рис. 1.10) начинает вращаться с постоянной угловой скоростью w против часовой стрелки из положения, при котором он образует с горизонтальной осью угол a. Проекция этого отрезка на вертикальную ось i в начальный момент времени 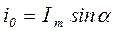. Когда отрезок повернется на угол 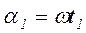, его проекция на ось i будет . Откладывая углы ,... 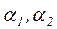по оси абсцисс, получим ряд значений синусоиды 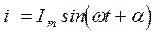. Угол a представляет собой начальную фазу. Повороту отрезка на угол 2p соответствует период синусоиды T.

Рис. 1.10

Таким образом, между синусоидальной функцией и вращающимся отрезком (радиусом-вектором) имеется однозначное соответствие. Если изменяющиеся по синусоидальному закону величины имеют одинаковую угловую частоту, то вращение радиусов-векторов можно не показывать. Итак, синусоидальным токам, напряжениям и ЭДС могут быть поставлены в соответствие векторы, длины которых равны амплитудам (или действующим значениям) синусоид, а сдвиг фаз между векторами равен сдвигу фаз между синусоидами. Совокупность векторов, изображающих синусоидальные токи, напряжения и ЭДС, называют векторной диаграммой. Положительный угол на векторной диаграмме отсчитывается против часовой стрелки, что позволяет судить о том, “отстает” данный вектор от другого или “опережает”. Поскольку при построении векторных диаграмм нас интересует лишь относительный сдвиг по фазе между синусоидальными функциями, то один из векторов можно расположить на диаграмме произвольно.

Действия над векторами упрощаются, если координаты концов записать в комплексной форме. Разместим векторную диаграмму на комплексной плоскости (рис. 1.11): пусть горизонтальная ось будет осью вещественных величин, а вертикальная - осью мнимых величин. Тогда вектор 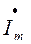, изображающий синусоидальный ток и называемый комплексной амплитудой тока, может быть записан в алгебраической форме:

.

В показательной форме

.

Переход от одной формы к другой осуществляется следующим образом:

.

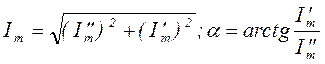Рис. 1.11 Рис. 1.12

Рассмотрим пример. Пусть необходимо найти ток

.

Токам и соответствует комплексные амплитуды

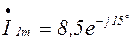и .

Построим указанные векторы в масштабе (M₁=2 A/см) и найдем их сумму по правилу сложения векторов (рис. 1.12) Получим вектор , модуль которого A, а начальная фаза - , т. е. .

Этот же результат можно получить аналитически. Действительно,

Переходя от комплексной амплитуды к мгновенному значению тока, получим

Дата добавления: 2015-05-08