
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Контрольная работа № I 2 страница
|
|
|
|
Таблица 6.9
Таблица термодинамических свойств перегретого пара
| Р, бар | ||||||||||
| t, º C | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | |
| 0,000999 0,001011 0,001042 0,001089 0,001156 | 2,1 210,9 420,1 632,8 852,4 | 0,0000 0,7020 1,3048 1,838 2,328 | 0,000999 0,001011 0,001042 0,001089 0,001155 | 3,1 211,8 420,9 633,4 852,6 | 0,0000 0,7018 1,3038 1,837 2,326 | 0,000998 0,001009 0,001041 0,001088 0,001153 0,001249 | 5,2 213,6 422,5 634,7 853,6 | 0,0004 0,700 1,302 1,835 2,322 2,789 | ||
| 0,1114 0,1255 0,1384 0,1511 0,1634 0,1755 0,1875 0,1995 0,2114 0,2232 | 6,539 6,757 6,949 7,122 7,282 7,429 7,569 7,701 7,827 7,947 | 0,0707 0,0812 0,0905 0,0993 0,1078 0,1161 0,1243 0,1325 0,1405 0,1484 | 6,283 6,530 6,735 6,916 7,080 7,231 7,373 7,506 7,633 7,755 | |||||||
| 0,0454 0,0519 0,0578 0,0633 0,0686 0,0737 0,0787 0,0836 0,0884 | 6,200 6,440 6,640 6,815 6,974 7,120 7,257 7,387 7,510 |
Окончание табл.6.9
| Р, бар | |||||||||
| t,º C | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | n, м3/кг | h, кДж/кг | S, кДж/(кгК) | n, м3/кг | h, кДж/кг | S, кДж/(кгК) |
| 0,000996 | 8,2 | 0,0004 | 0,000995 | 10,2 | 0,0004 | 0,000993 | 15,2 | 0,0008 | |
| 0,001008 | 216,2 | 0,6992 | 0,001007 | 218,0 | 0,698 | 0,001005 | 222,3 | 0,695 | |
| 0,001040 | 424,9 | 1,3996 | 0,001038 | 426,5 | 1,298 | 0,001036 | 430,4 | 1,294 | |
| 0,001086 | 636,6 | 1,832 | 0,001084 | 638,0 | 1,830 | 0,001081 | 641,3 | 1,824 | |
| 0,001150 | 855,0 | 2,317 | 0,001148 | 856,0 | 2,314 | 0,001144 | 858,3 | 2,306 | |
| 0,001244 | 1085,7 | 2,781 | 0,001240 | 2,776 | 0,001233 | 2,765 | |||
| 0,02429 | 5,788 | 0,001397 | 3,244 | 0,001377 | 3,222 | ||||
| 0,03003 | 6,126 | 0,02247 | 5,940 | 0,01150 | 5,442 | ||||
| 0,03438 | 6,356 | 0,02646 | 6,207 | 0,01568 | 5,878 | ||||
| 0,03821 | 6,552 | 0,02979 | 6,416 | 6,139 | |||||
| 0,04177 | 6,722 | 0,03281 | 6,596 | 0,02080 | 6,346 | ||||
| 0,04516 | 6,876 | 0,03566 | 6,756 | 0,02291 | 6,521 | ||||
| 0,04844 | 7,019 | 0,03837 | 6,901 | 0,02490 | 6,677 | ||||
| 0,05161 | 7,152 | 0,04097 | 7,038 | 0,02677 | 6,822 | ||||
| 0,05475 | 7,280 | 0,04354 | 7,167 | 0,02857 | 6,956 |
Тогда энтальпия влажного пара после турбины
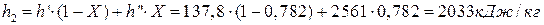 ,
,
где  = 137,8 кДж/кг – энтальпия воды на линии насыщения и
= 137,8 кДж/кг – энтальпия воды на линии насыщения и  = 2561 кДж/кг – энтальпия сухого насыщенного пара, взятые также из табл. 6.8 при давлении Р2 = 0,05 бар.
= 2561 кДж/кг – энтальпия сухого насыщенного пара, взятые также из табл. 6.8 при давлении Р2 = 0,05 бар.
Необратимые потери при действительном расширении пара в турбине 1-2Д учитываются внутренним относительным КПД турбины
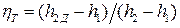 ,
,
откуда, при заданном 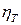 = 0,89, находим энтальпию в конце действительного расширения пара:
= 0,89, находим энтальпию в конце действительного расширения пара:
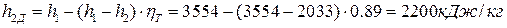 .
.
Степень сухости пара в точке 2Д:
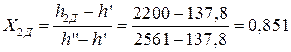 .
.
Энтропия пара в точке 2Д:
 .
.
Повышение энтальпии питательной воды в насосе:
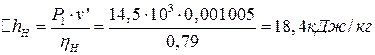 ,
,
где Р1 = 14,5·103 кПа – давление питательной воды после насоса; 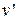 = 0,001005 м3/кг – удельный объем воды перед насосом (при Р2 = 0,05 бар);
= 0,001005 м3/кг – удельный объем воды перед насосом (при Р2 = 0,05 бар); 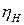 = 0,79 – внутренний относительный КПД насоса (задан).
= 0,79 – внутренний относительный КПД насоса (задан).
Энтальпия воды за питательным насосом:
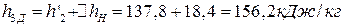 .
.
Внутренний относительный КПД насоса
 ,
,
откуда находим энтальпию питательной воды после теоретического сжатия:
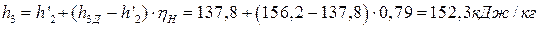 .
.
Процессы теоретического 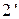 -3 и действительного
-3 и действительного 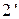 -3Д сжатия воды в питательном насосе изображены в hS – диаграмме на рис.6.8.
-3Д сжатия воды в питательном насосе изображены в hS – диаграмме на рис.6.8.
Термический КПД цикла Ренкина:
 .
.
Так как работа пара в турбине
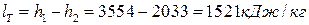
много больше работы сжатия воды в насосе.
 ,
,
то для приближенных расчетов работой сжатия воды в насосе пренебрегают ( ), тогда приближенно:
), тогда приближенно:
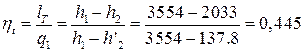 .
.
С учетом внутренних необратимых потерь в турбине и в насосе находим внутреннюю работу ПТУ:
 .
.
Теоретическая работа ПТУ:
 .
.
Следовательно, из-за необратимых потерь теряется работоспособность ПТУ на
 .
.
Эффективная мощность ПТУ:
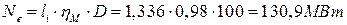 ,
,
где  = 0,98 – механический КПД ПТУ и D = 100 кг/с – расход пара через турбину – заданы.
= 0,98 – механический КПД ПТУ и D = 100 кг/с – расход пара через турбину – заданы.
7. Контрольная работа №2
Задача 7.1. Внутри стальной горизонтальной трубы (λст = 20 Вт/м·К) со скоростью W1 течет вода с температурой t1. Снаружи труба охлаждается воздухом (свободная конвекция), температура воздуха – t2. Определить коэффициенты теплоотдачи α1 и α2 соответственно от воды к внутренней стенке трубы и от наружной стенки к воздуху; линейный коэффициент теплопередачи Кl и линейный тепловой поток ql, если внутренний диаметр трубы d1, внешний – d2. Исходные данные взять из табл.7.1.
Указание. Для определения α2 в первом приближении температуру наружной поверхности tw2 принять равной tw1 = 0,5(t1+t2).
Таблица 7.1
Исходные данные к задаче 7.1
| Последняя цифра шифра | t1, ºC | W1, м/с | Предпоследняя цифра шифра | t2, ºC | м | |
| d1 | d2 | |||||
| 0,01 | 0,10 | 0,11 | ||||
| 0,05 | 0,11 | 0,12 | ||||
| 0,10 | 0,12 | 0,13 | ||||
| 0,15 | 0,13 | 0,14 | ||||
| 0,20 | 0,14 | 0,15 | ||||
| 0,25 | 0,15 | 0,16 | ||||
| 0,30 | 0,16 | 0,17 | ||||
| 0,35 | 0,17 | 0,18 | ||||
| 0,40 | 0,18 | 0,19 | ||||
| 0,45 | 0,19 |
Указание. Для определения коэффициентов теплоотдачи физические свойства воды и воздуха взять из табл.7.2, 7.3.
Таблица 7.2
Физические свойства воздуха при нормальном давлении [8]
и теплоемкость золы [9]
| t, ºC | Срm, кДж/кг·К | λ, Вт/м·К | ν·106, м2/с | Рr | Сз, кДж/кг·К |
| 1,003 | 0,0244 | 13,28 | 0,707 | - | |
| 1,003 | 0,0259 | 15,06 | 0,703 | - | |
| 1,003 | 0,0276 | 16,96 | 0,699 | - | |
| 1,004 | 0,0290 | 18,97 | 0,696 | - | |
| 1,004 | 0,0305 | 21,09 | 0,692 | - | |
| 1,005 | 0,0321 | 23,13 | 0,688 | 0,810 | |
| 1,006 | 0,0334 | 25,45 | 0,686 | - | |
| 1,007 | 0,0349 | 27,80 | 0,684 | - | |
| 1,008 | 0,0364 | 30,09 | 0,682 | - | |
| 1,009 | 0,0378 | 32,49 | 0,681 | - | |
| 1,010 | 0,0393 | 34,85 | 0,680 | 0,845 | |
| 1,014 | 0,0427 | 40,61 | 0,677 | - | |
| 1,018 | 0,0460 | 48,33 | 0,674 | 0,880 | |
| 1,022 | 0,0491 | 55,46 | 0,676 | - | |
| 1,027 | 0,0521 | 63,09 | 0,678 | 0,900 | |
| 1,038 | 0,0574 | 79,38 | 0,687 | 0,916 | |
| 1,049 | 0,0622 | 96,89 | 0,699 | 0,935 | |
| 1,060 | 0,0671 | 115,4 | 0,706 | 0,947 | |
| 1,069 | 0,0718 | 134,8 | 0,713 | 0,960 | |
| 1,080 | 0,0763 | 155,1 | 0,717 | 0,971 | |
| 1,090 | 0,0807 | 177,1 | 0,719 | 0,984 | |
| 1,099 | 0,0850 | 199,3 | 0,722 | 0,996 | |
| 1,107 | 0,0915 | 233,7 | 0,724 | 1,005 |
Таблица 7.3
Физические свойства воды на линии насыщения [8]
| t, ºC | ρ, кг/ м3 | Ср, кДж/кг·К | λ, Вт/м·К | ν·106, м2/с | β·104, 1/К | Рr |
| 999,9 | 4,212 | 0,551 | 1,789 | -0,63 | 13,67 | |
| 998,2 | 4,183 | 0,599 | 1,006 | +1,82 | 7,02 | |
| 992,2 | 4,174 | 0,635 | 0,659 | 3,87 | 4,31 | |
| 983,2 | 4,179 | 0,659 | 0,478 | 5,11 | 2,98 | |
| 971,8 | 4,195 | 0,674 | 0,365 | 6,32 | 2,21 | |
| 958,4 | 4,220 | 0,683 | 0,295 | 7,52 | 1,75 | |
| 943,1 | 4,250 | 0,686 | 0,252 | 8,64 | 1,47 | |
| 926,1 | 4,287 | 0,685 | 0,217 | 9,72 | 1,26 | |
| 907,4 | 4,346 | 0,683 | 0,191 | 10,7 | 1,10 | |
| 886,9 | 4,417 | 0,674 | 0,173 | 11,9 | 1,00 | |
| 863,0 | 4,505 | 0,663 | 0,158 | 13,3 | 0,93 | |
| 840,3 | 4,614 | 0,645 | 0,149 | 14,8 | 0,89 | |
| 813,6 | 4,756 | 0,628 | 0,141 | 16,8 | 0,87 | |
| 784,0 | 4,949 | 0,605 | 0,135 | 19,7 | 0,87 | |
| 750,7 | 5,230 | 0,574 | 0,131 | 23,7 | 0,90 | |
| 712,5 | 5,736 | 0,540 | 0,128 | 29,2 | 0,97 | |
| 667,1 | 6,574 | 0,506 | 0,128 | 38,2 | 1,11 | |
| 610,1 | 8,165 | 0,457 | 0,127 | 53,4 | 1,39 | |
| 528,0 | 13,98 | 0,395 | 0,126 | 2,35 |
РЕШЕНИЕ (вариант 99).
Для вынужденной конвекции воды в трубе определяется режим движения по числу Рейнольдса:
 ,
,
то-есть режим движения турбулентный.
 (7.1)
(7.1)
При ламинарном режиме (Re1<2300) уравнение подобия конвективной теплоотдачи имеет вид:
 (7.2)
(7.2)
и при переходном режиме (Re1 = 2300…104):
 (7.3)
(7.3)
Здесь 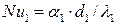 - число Нуссельта:
- число Нуссельта:
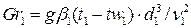 - число Грасгофа;
- число Грасгофа;
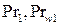 - числа Прандтля воды соответственно при температуре воды t1 и температуре внутренней стенки трубы tw1, которая в первом приближении принимается равной tw1 = tw2 = 0.5(t1+t2) = 110ºC (Prw1 = 1.6);
- числа Прандтля воды соответственно при температуре воды t1 и температуре внутренней стенки трубы tw1, которая в первом приближении принимается равной tw1 = tw2 = 0.5(t1+t2) = 110ºC (Prw1 = 1.6);
ν1 = 0,153 ·10-6 м2/с – коэффициент кинематической вязкости воды находится по табл.7.3 при t1 = 210ºC;
λ1 = 0,655 Вт/м·К – коэффициент теплопроводности воды;
g = 9,81м/ с2 – ускорение свободного падения;
β1 = 14,1·10-4 1/К – коэффициент объемного расширения воды,
итак, по уравнению (7.1) для турбулентного режима:
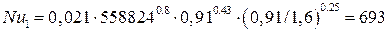 .
.
Коэффициент конвективной теплоотдачи от воды:
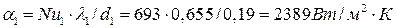 .
.
Число Грасгофа для воздуха:
 ,
,
где для воздуха  .
.
Коэффициент свободноконвективной теплоотдачи к воздуху определяется из уравнения подобия:
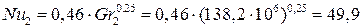 ,
,
 ,
,
где  - коэффициент теплопроводности воздуха при t2 = 10ºC по табл.7.2;
- коэффициент теплопроводности воздуха при t2 = 10ºC по табл.7.2;
 - коэффициент кинематической вязкости воздуха.
- коэффициент кинематической вязкости воздуха.
Линейный коэффициент теплопередачи:

Линейный тепловой поток:
 .
.
Температура внутренней поверхности трубы:
 .
.
Температура наружной поверхности трубы:
 .
.
Второе приближение:
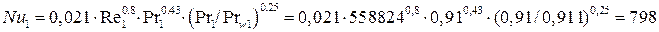 ;
;
 ;
;
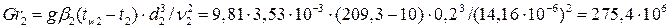 ;
;
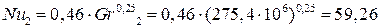 ;
;
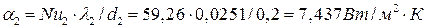 ;
;
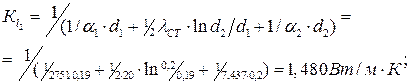
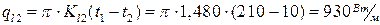 ;
;
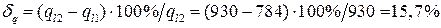 .
.
Расхождения между вторым и первым приближениями велико, следовательно, необходимо третье приближение.
Третье приближение.
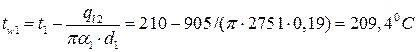 ;
;
 .
.
Так как по сравнению со вторым приближением tw1 изменилась всего на 0,1К, то можно принять Nu1 = 59.3 и α1 = 2751 Вт/м2·К по второму приближению;
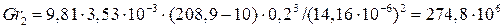 ;
;
 ;
;
 ;
;
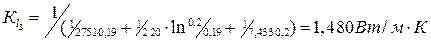 ;
;
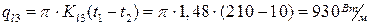 ;
;
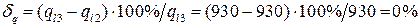 .
.
Это означает, что расчет в третьем приближении точный. Задача решена.
Задача 7.2. Определить поверхность нагрева рекуперативного газовоздушного теплообменника при прямоточной и противоточной схемах движения теплоносителей, если массовый расход нагреваемого воздуха m2, средний коэффициент теплопередачи от газов к воздуху К, начальные и конечные температуры газов и воздуха соответственно: 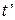 1 и
1 и  1,
1, 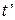 2 и
2 и  2. Исходные данные взять из табл.7.4.
2. Исходные данные взять из табл.7.4.
Изобразить графики изменения температур теплоносителей для обоих случаев.
Таблица 7.4
Исходные данные к задаче 7.2
| Последняя цифра шифра | m2, кг/с | К, Вт/м2·К | Предпоследняя цифра шифра | 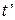 1,
ºC 1,
ºC
|  1,
ºC 1,
ºC
| 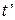 2,
ºC 2,
ºC
|  2,
ºC 2,
ºC
|
РЕШЕНИЕ (вариант 99).
 Рис. 7.2. Противоток.
Рис. 7.2. Противоток.
|
Графики изменения температур теплоносителей приведены на рис.7.1 и 7.2.
 Рис. 7.1. Прямоток.
Рис. 7.1. Прямоток.
|
Тепловой поток, воспринятый нагреваемым воздухом:
 ,
,
где средняя, массовая, изобарная теплоемкость воздуха
 .
.
Здесь средние теплоемкости 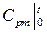 взяты из табл.7.2 для воздуха.
взяты из табл.7.2 для воздуха.
Большая и меньшая разности температур между теплоносителями для прямотока:
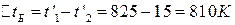 ;
;
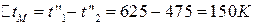 ;
;
 , поэтому средняя разность температур между теплоносителями определяется как средне-логарифмическая:
, поэтому средняя разность температур между теплоносителями определяется как средне-логарифмическая:
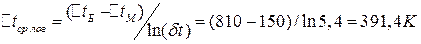 .
.
Необходимая поверхность нагрева прямоточного теплообменника:
 .
.
То же самое для противотока:
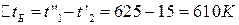 ;
;
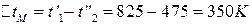 ;
;
 ;
;
то-есть среднюю разность температур между теплоносителями с достаточной точностью можно посчитать, как средне-арифметическую:
 .
.
Необходимая поверхность нагрева противоточного теплообменника:
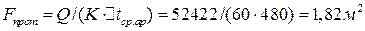 .
.
Среднюю разность температур называют “движущей силой” теплопередачи, при противотоке она больше ( ,
,  ), поэтому при одинаковых условиях противоточный теплообменник компактнее (Fпрот = 1,82 м2)<(Fпрям = 2,23 м2), требует для своего изготовления меньших затрат материалов (конструктивный расчет).
), поэтому при одинаковых условиях противоточный теплообменник компактнее (Fпрот = 1,82 м2)<(Fпрям = 2,23 м2), требует для своего изготовления меньших затрат материалов (конструктивный расчет).
Если же имеется готовый теплообменник, то при одинаковых условиях получится Qпрот>Qпрям (поверочный расчет) – из-за более высокой “движущей силы” при противотоке. Кроме того, как видно из рис.7.2, при противотоке можно нагреть холодный теплоноситель до температуры  2>
2>  , что невозможно в принципе при прямотоке (см. рис. 7.1).
, что невозможно в принципе при прямотоке (см. рис. 7.1).
ЗАДАЧА 7.3. Задано топливо и паропроизводительность котлоагрегата D. Определить состав топлива по рабочей массе и его низшую теплоту сгорания, способ сжигания топлива, тип топки, значение коэффициента избытка воздуха в топке αТ и в уходящих из топки газах αух по величине присоса воздуха по газовому тракту ∆α; найти теоретически необходимое количество воздуха V0 для сгорания 1кг (1м3) топлива и объемы продуктов сгорания при αух, а также энтальпию уходящих газов Iух при заданной температуре уходящих газов tух и их влагосодержании dух. Исходные данные выбрать из табл.7.5.
Таблица 7.5
Исходные данные к задаче 7.3
| Последняя цифра шифра | Вид топлива | Предпослед-няя цифра шифра | D, T/ч | ∆α | tyx, ºC |
| Кузнецкий уголь Г (каменный, газовый) | 0,15 | ||||
| Мазут малосернистый | 0,16 | ||||
| Газ из газопровода “Средняя Азия - Центр” | 0,18 | ||||
| Челябинский уголь БЗ (бурый) | 0,20 | ||||
| Мазут сернистый | 0,22 | ||||
| Газ из газопровода “Бухара – Урал” | 0,24 | ||||
| Канско–Ачинский уголь Б2 (бурый) | 0,26 | ||||
| Мазут высокосернистый | 0,28 | ||||
| Газ из газопровода “Саратов – Москва” | 0,30 | ||||
| Экибастузский уголь СС (бурый, слабоспекающийся) | 0,32 |
Таблица 7.6
|
|
|
|
|
Дата добавления: 2015-05-08; Просмотров: 617; Нарушение авторских прав?; Мы поможем в написании вашей работы!