На защиту выносятся 3 страница

8-^аЫ

и

Рис. 2.18. Тарировочная зависимость.

Ео² — длина отрезка на оси Е²; В — тангенс угла наклона. Показатель степени п определяется из условия лучшей аппроксимации тарировочных

2 2 п

значений зависимостью Е =Ео + В*и.В широком диапазоне условий величина п лежит в пределах от 0,4 до 0,5.

Интенсивность продольной составляющей скорости получается непосредственно с помощью обычной нити, расположенной
перпендикулярно направлению средней скорости. При этом интенсивности двух других составляющих скорости малы. Интенсивность продольной компоненты можно определить путем разложения в ряд формулы (1) по малым параметрам и' (правая часть) и е' (левая часть) и ограничиваясь первым членом разложения. В результате получим:

где - среднеквадратичное напряжение сигнала нагретой нити при

данной скорости потока; Е - среднее напряжение и Е'_а = 0,95* Е₀, где Е_й -

среднее напряжение при нулевой скорости потока.

Обращает на себя внимание, что заключенный в скобки коэффициент чувствительности термоанемометра к пульсациям скорости, зависит от средней скорости потока, что необходимо учитывать в практической работе.

Метод термоанемометрии также позволяет производить измерения осредненных и пульсационных характеристик, спектров и пространственно- временных корреляций в областях срыва [120].

В данной работе для измерения средней и пульсационной продольной составляющей скорости потока использовалось два термоанемометра постоянной температуры AN-1003 фирмы A.A.Labs (Израиль) на трубе Т-324 и Dantec 54Т30 на трубе МТ-324.

Аналоговый сигнал с моста термоанемометра переводился в цифровую форму 16-и разрядным аналого-цифровым преобразователем National Instruments 6523 (АЦП) с BNC коннектором, линеаризовался и записывался в память персонального компьютера как зависимость мгновенной величины сигнала (и) от времени (/).

Подходящий датчик для определенного эксперимента изготавливался в Институте теоретической и прикладной механики. Он имел высокую чувствительность к скорости потока, а также наивысший частотный отклик. Каждый датчик состоял из стального нержавеющего корпуса с выведенными сквозь него коническими державками, которые имели диаметр на конце порядка 0,1 миллиметра. Чувствительный элемент датчика — это вольфрамовая проволочка диаметром 5 микрон покрытая золотом, которая приваривалась на точечную сварку к заострённым концам датчика (рис. 2.19). Длина чувствительного участка около 2 мм. Такой датчик использовался, так как был специально разработан для высокотурбулентных потоков. Во всех измерениях датчик был ориентирован перпендикулярно направлению потока и с помощью координатного устройства мог перемещаться во всех трех направлениях X, У, Ъ.

Рис. 2.19. Схема датчика термоанемометра.

Датчик тарировался в свободном потоке напротив трубки Пито- Прандтля, соединенной со спиртовым микроманометром (рис. 2. 20). Связь средней скорости с показаниями микроманометра дается следующим образом:

?*дР / /

у_т; Г-А.»

где АР мм - показания микроманометра, р_д ^кг/ ₃ - плотность воздуха,

/ м

Ра, ^кг/ ъ ~ плотность спирта, % ^м/ ₂- ускорение свободного падения, а­/ м / сек

угол наклона микроманометра. Тем самым обеспечивалась точность

измерения средней скорости порядка +/-1%.

Рис. 2. 20. Спиртовой микроманометр.

При калибровке датчика использовался модифицированный закон Кинга:

и= к, * (Е² - Е²)^ш + к²* (Е- Е₀)^т,

где Е и Е₀ - выходные напряжения с моста термоанемометра при скорости потока и Ф 0 и в покое соответственно, к_ь к₂ и п - константы, определяемые эмпирически. Первый член с точностью до определения констант соответствует приведенному выше закону Кинга, а второй - добавлен для учета свободной конвекции при малых скоростях потока и несколько расширяет диапазон надежных измерений у стенки.

2.3.3. Методика пневмометрических измерений.

Вихревые структуры, возникающие над крылом, по-видимому, должны были отразиться на распределении статического давления по поверхности. Для малоразмерных беспилотных летательных аппаратов это представляется особенно важным, потому что автоматические системы управления летательным аппаратом нуждаются в надежной информации о текущем значении угла атаки самолета. Наиболее надежным и легко осуществимым способом получения такой информации считается способ измерения распределения давления по обтекаемому телу.

В данной работе для измерения статического давления был использован специальный насадок - подпружиненная трубочка диаметром 0.8 мм, запаянная с переднего торца и имевшая отверстие на боковой стенке (рис. 2.21). Насадок устанавливался на державке координатного комплекса, позволяющего перемещать датчик в трех плоскостях X, У, Z и получать информацию в большом количестве точек на поверхности модели. С помощью пневмотрасс насадок и трубка Пито-Прандтля соединялись со спиртовым микроманометром. Давление измерялось с помощью микроманометра как разница между полным давлением в насадке Пито- Прандтля, установленном в рабочей части трубы, и насадком, описанным выше. При измерениях плоскость А (рис. 2.15) всегда прилегала к поверхности модели. Сравнительные измерения статического давления с помощью дренажа и таким датчиком показали, что погрешность не превышает 5% от скоростного напора.

Коэффициент давления С_р вычислялся по формуле:

^ср ⁼ (Р-Ро)!

где С_р - коэффициент давления; р₀ - полное давление; р — статическое давление на поверхности модели; д — скоростной напор.

Рис. 2. 21. Схема приемника статического давления. 1 - поверхность модели; 2 - насадок статического давления; 3 - гибкая трубка; 4 — державка, закрепляющаяся на штангу датчика АИК.

Глава III. ВИХРЕВАЯ СТРУКТУРА ОТРЫВНЫХ ТЕЧЕНИЙ НА ПРЯМОМ И СКОЛЬЗЯЩЕМ КРЫЛЕ.

Данная глава посвящена экспериментальному изучению вихревых структур, возникающих внутри области срыва на моделях прямых крыльев и в зависимости от геометрии крыла и угла скольжения. Дело в том, что отрыв потока на крыле с нулевым углом скольжения исследован уже достаточно хорошо, однако данных о влиянии этого фактора на вихревую картину течения пока известно очень мало. В тоже время, малоразмерные летательные аппараты могут попадать одновременно в режим срыва и в режим скольжения из-за большого влияния порывов ветра на их обтекание и поэтому такие режимы требуют внимательного изучения.

Результаты проведенных экспериментов, описанных в данной главе, были опубликованы в работе [121].

3.1. Условия проведения эксперимента.

Эксперименты были проведены в дозвуковых аэродинамических трубах Т-324 и МТ-324 на моделях крыльев № 1 — 4. Каждая модель помещалась в рабочую часть и жестко закреплялась с помощью специального кронштейна к нижней поверхности рабочей части. Крепления крыла, кронштейн имели удобообтекаемый профиль и на поток существенного влияния не оказывали. Основным методом исследований картины течения была «саже-масляная» визуализация. Следует отметить, что картина течения на поверхности модели сильно зависит от угла атаки. В экспериментах модели устанавливались под достаточно большими углами атаки, при которых наблюдается срыв потока с передней кромки. Этот угол атаки определялся при помощи наклеенных на поверхность модели шелковинок, показывающих направление потока. Дело в том, что при достижении угла атаки, на котором происходит срыв, на поверхности модели возникает возвратное течение от задней кромки к передней. Поиск угла атаки, на котором происходит срыв, проводился на моделях, установленных под нулевым углом скольжения. Визуальное обнаружение возвратного течения по направлению шелковинок от задней кромки к передней служило признаком существования срыва потока. Затем шелковинки убирались, и все последующие эксперименты проводились уже на данном угле атаки, который не изменялся в ходе продувки. Объектом исследований была структура течения внутри области отрыва. После проведения эксперимента характерные картины течений фотографировались.

3.2. Зависимость структуры обтекания от удлинения крыла.

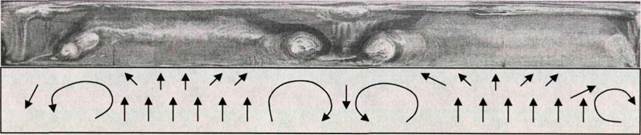
Описанные в этом разделе исследования должны были дать ответ на вопрос о влиянии краевых условий на образование парных крупномасштабных вихрей в области срыва. Дело в том, что в упоминаемых выше работах обнаруживалась только одна пара вихрей в области срыва [54, 57, 62, 64, 95, 96]. Однако, при отрыве турбулентного пограничного слоя в задней части крыла всегда образовывалось несколько пар вихрей. Поэтому высказывались предположения, что в области срыва большое влияние оказывают краевые эффекты, и поэтому вихри образуются только у боковых кромок модели. Для того чтобы проверить эти предположения, эксперименты были проведены на моделях с разным удлинением, что позволило оценить влияние краевых эффектов на картину течения. Полученные результаты показаны на рис. 3.1. Здесь приведены картины течения при срыве потока на моделях крыльев с удлинением от 0,7 до 9,8 в диапазоне скоростей потока от 10 до 30 м/с. В этих экспериментах впервые было зарегистрировано образование при срыве не одной, а двух пар вихрей на крыле большого удлинения. Направление потока — сверху вниз.

На рис. 3.1 (а) показана картина течения на крыле № 1 малого удлинения. Скорость потока составляла 11,5 м/с, угол атаки - а = 21°. Яе = 2,2 * 10⁵ по хорде. Хорошо видны два вихря вблизи передней кромки по бокам модели. Впервые аналогичные картины были опубликованы в работах В.Я. Нейланда с соавторами [61, 62, 63]. Было показано, что «возникновение при некотором угле атаки отрыва потока в носовой части крыла приводило при сильном взаимодействии концевых вихревых жгутов с пограничным слоем к скачкообразному развитию сложного вихревого течения с обширной циркуляционной зоной в середине крыла. Дальнейшее увеличение угла атаки не сказывалось на положении и размерах циркуляционной зоны» [61,62, 63]. Следует пояснить, что в указанных работах угол атаки а модели постепенно увеличивался в ходе эксперимента, в то время, как в нашем случае модель устанавливалась на выбранном угле атаки до начала продувки. Тем не менее, результаты очень похожи.

На рис. 3.1 (б) показана картина течения на модели № 2 умеренного удлинения. Скорость потока составляла 10 м/с, угол атаки - а =14°. Яе = 0,7 * 10⁵. В области отрыва на поверхности модели также присутствуют два вихря, и они расположены в центральной и задней части модели. Между вихрями существует возвратное течение от задней кромки вихря к передней, и затем растекание от центра модели в трансверсальном направлении, вдоль линии растекания направо и налево к фокусам вихрей. В передней части модели существует застойная зона, расположенная между линией отрыва потока у передней кромки модели и уже упомянутой линией растекания.

На рис. 3.1 (в) показана картина течения на модели № 3 среднего удлинения. Скорость потока составляла 30 м/с, угол атаки - а =12°. Яе = 3,9 * Ю³. В отличие от описанных выше результатов, в данном случае не наблюдается ярко выраженных фокусов вихрей, но в целом сохраняется течение с двумя вихрями, наиболее хорошо заметное по краям модели.

На рис. 3.1 (г) показана картина течения на модели № 4 большого удлинения. Скорость потока составляла 29 м/с, угол атаки - а = 12°. Яе = 1,9 * 10⁵. Оказалось, что в данном случае (при увеличении удлинения до 9,8) в области срыва возникает две пары вихрей. Эти результаты показывают, на взгляд автора, что появление вихрей в области срыва связано не только с

влиянием краевых эффектов. По-видимому, есть некий предельный размер вихревой пары, и если размах крыла больше этого предельного размера, то образуется уже не одна, а две вихревые пары.

•«-------- с—х	—►
о.	.О
\ т X

(а). Крыло малого удлинения X = 0,7. (б). Крыло умеренного удлинения X = 2.

4 --------------- - '
	\ \ 1 i	г к i	/ к ¿	к i

(в). Крыло среднего удлинения X = 4,8.

(г). Крыло большого удлинения X = 9,8. Рис. 3.1. Зависимость вихревой структуры течения от удлинения крыла.

3.3. Процессы перестройки структуры вихревого течения на поверхности моделей крыльев разного удлинения в зависимости от угла скольжения.

Целью, проведенных экспериментов, описанных в данной главе, было изучение вихревых структур, возникающих внутри области срыва на моделях прямых крыльев, и их зависимость от угла скольжения. Дело в том, что отрыв потока на крыле с нулевым углом скольжения исследован уже достаточно хорошо, однако данных о влиянии этого фактора на вихревую картину течения пока известно очень мало. В то же время малоразмерные летательные аппараты могут попадать одновременно в режимы срыва и скольжения из-за большого влияния порывов ветра на их обтекание, и поэтому такие режимы требуют внимательного изучения.

Для исследования влияния угла скольжения (угол между направлением набегающего потока и передней кромкой) при срывном режиме обтекания модели поворачивались на своих подставках так, чтобы этот угол составлял ноль, 15, 30 или 45 градусов. Данные эксперименты проводились на трех моделях крыльев № 2, 3 и 4. Принципиальное различие между этими моделями в том, что при обтекании без скольжения на крыле № 2 и № 3 образуется одна пара вихрей, а на модели № 4 большого удлинения - две пары вихрей. Скорость потока в экспериментах была в диапазоне от 15 м/с до 30 м/сек, угол атаки 12 градусов.

3.3.1. Крыло умеренного удлинения.

На рис. 3.2 показаны картины течения на поверхности модели № 2. Скорость набегающего потока 15 м/с. Яе = 1 * 10⁵. Угол атаки составлял а =12°. При нулевом угле скольжения Р (рис. 3.2, а) на поверхности модели наблюдается возвратное течение от задней кромки крыла к передней и растекание из центральной части к боковым кромкам. При повороте модели на угол скольжения 15 градусов картина течения существенно изменилась (рис. 3.2, б). Образовалась так называемая «застойная зона» вблизи передней кромки и один крупномасштабный вихрь. При увеличении угла скольжения до 30 градусов (рис. 3.2, в) «застойная зона» значительно уменьшилась в размерах и сместилась ближе к левому краю. На большей части крыла наблюдается присоединённое течение.

б. Угол скольжения (3=15.

Рис. 3.2. Зависимость вихревой структуры от угла скольжения на крыле

в. Угол скольжения (3 = 30.

а. Угол скольжения (3 = 0.

удлинения Х = 2.

3.3.2. Крыло среднего удлинения.

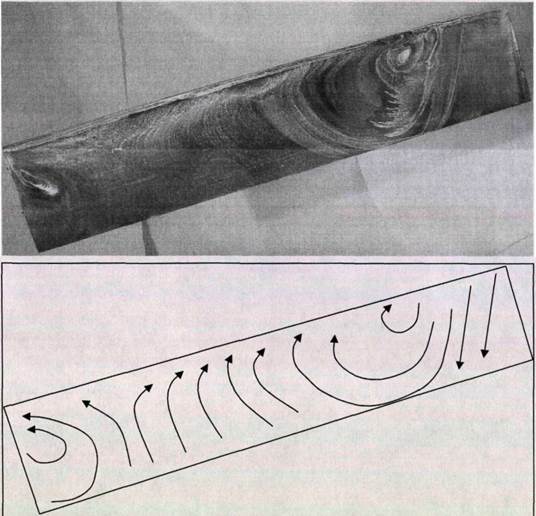
На рис. 3.3 показаны картины течения на поверхности модели № 3 с удлинением 4,8. Скорость набегающего потока 30 м/с. Яе = 3,9 * 10^э. Угол атаки составлял а =12°. При нулевом угле скольжения (рис. 3.3, а) картина течения при срыве характеризуется существованием одной пары вихрей, хорошо заметных у боковых кромок модели. При повороте модели на угол скольжения 15° картина течения существенно изменилась (рис. 3.3, б). Размеры левого вихря значительно уменьшились, при этом части модели доминирует правый вихрь, закручивающий поток по часовой стрелке. Еще более кардинально изменилась картина течения при увеличении угла скольжения до 30°. В этом случае на поверхности модели вместо пары вихрей остался только один вихрь, сдвинувшийся к левому краю модели, и вращающийся по часовой стрелке (рис. 3.3, в). При достижении угла скольжения р = 45° на всей поверхности наблюдается присоединенное течение (рис. 3.3, г).

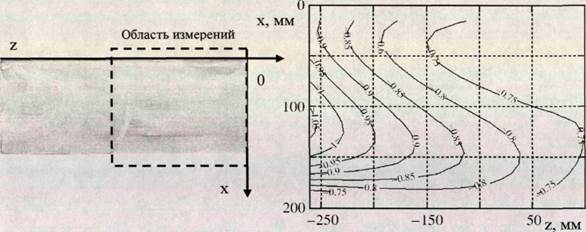
С целью сопоставить картины саже-масляной визуализации и распределение давления по поверхности крыла, были проведены пространственные измерения с помощью насадка статического давления. Измерения проводились с шагом 10 мм по хорде и по размаху. Область измерения простиралась от оси симметрии модели до, приблизительно, Ул части размаха. Измерения показали, что для прямого крыла без скольжения (рис. 3.4, а) при срыве потока распределение давления, даже вблизи от оси симметрии крыла, носит трехмерный характер вследствие влияния концевого вихря, но градиенты давления небольшие. На передней кромке крыла обтекаемого со скольжением (рис. 3.4, б) в зоне центра вихря давление минимально и увеличивается от центра к краю крыла и от передней кромки к задней. Кривая распределения давления по оси симметрии вдоль хорды (рис. 3.4, в) для крыла без скольжения имеет вид, характерный для срывного обтекания, а для крыла с углом скольжения Р = 30°, из вида кривой следует, что в этом сечении срыва нет, течение присоединенное. Оказалось, что на скользящих крыльях области отрывного вихревого обтекания могут близко соседствовать с областями безотрывного присоединенного течения. Это обстоятельство накладывает более строгие требования к выбору места установки датчиков давления для систем, дающих информацию о угле атаки крыла. Датчики должны располагаться не только по линии хорды, но и по размаху крыла. Конкретное положение и требуемое количество датчиков зависят как от стреловидности крыла, так и от его удлинения.

и,

а. Угол скольжения ß = 0.

б. Угол скольжения ß = 15.

а

в. Угол скольжения ß = 30.

г. Угол скольжения р = 45.

Рис. 3.3. Зависимость вихревой структуры от угла скольжения на крыле

и.

^ г

<

¿Г

удлинения А, = 4,8.

а) Изобары статического давления. Угол скольжения Р = 0^и.

X, мм Область измерений

200 -300

-200 -100 б) Изобары статического давления. Угол скольжения р

Ср

-1.4 -0.8 -0.2

в) Распределение давления вдоль хорды по оси симметрии модели.

Рис. 3.4. Распределение статического давления на поверхности модели с

= 30°.

удлинением X = 4,8.

3.3.3. Крыло большого удлинения.

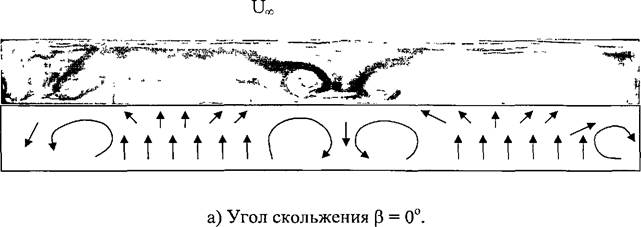
Далее исследовалось влияние угла скольжения на модели № 4 с большим удлинением, равным X = 9,8. Скорость набегающего потока 29 м/с. Яе = 1,9 * 10⁵. Угол атаки составлял а =12°. На поверхности модели при обтекании без скольжения (рис. 3.5, а) в области отрыва имеются две вихревые пары, как это было отмечено выше. При р = 15° в левой части модели сохранилась вихревая пара, но произошло присоединение потока на правой части модели (рис. 3.5, б). Здесь линии тока на поверхности модели направлены от передней кромки к задней, но вдоль задней кромки существует течение в левую часть модели к фокусу вихря. При увеличении угла скольжения Р до 30° вихри на поверхности модели полностью исчезли, (рис. 3.5, в), однако сохранилось течение справа налево вдоль задней кромки модели.

в) Угол скольжения 30°.

Рис. 3.5. Зависимость вихревой структуры от угла скольжения на крыле

удлинения X = 9,8.

3.4. Выводы к главе III.

1. Проведены экспериментальные исследования вихревых структур, возникающих внутри области срыва на моделях прямых крыльев в зависимости от геометрии крыла и угла скольжения.

2. Получены картины течений на поверхности моделей крыльев разного удлинения и при разных углах скольжения.

3. Показаны процессы перестройки структуры вихревого течения на поверхности моделей крыльев разного удлинения в зависимости от угла скольжения.

4. Установлено, что на крыле большого удлинения при отрывном течении «, образуются две пары вихрей, т.е. можно сделать вывод, что появление таких парных вихрей не является влиянием краевых эффектов, но является фундаментальным свойством отрывных течений.

5. Показано, что появление угла скольжения приводит к возникновению несимметричных вихревых структур, и, при большом угле скольжения, к их полному исчезновению.

Глава IV. УПРАВЛЕНИЕ ОБТЕКАНИЕМ МОДЕЛИ С ПОМОЩЬЮ ЛОКАЛЬНОГО ВДУВА ВОЗДУХА.

Изучение отрывных течений имеет большое практическое значение для нового направления в авиации - малоразмерных летательных аппаратов различного назначения, которые в настоящее время получают все более широкое распространение. Связано это с несколькими причинами: их экономичностью, уникальными летными характеристиками, малой уязвимостью и т.д. Полетное число Рейнольдса по хорде крыла у таких летательных аппаратов лежит в диапазоне Яе = 10⁵ - 10⁶. В настоящее время существует настоятельная необходимость улучшения летных качеств малоразмерных летательных аппаратов. Дело в том, что используемые на таких аппаратах классические дозвуковые профили крыла на малых (докритических) углах атаки имеют большое сопротивление в результате образования обширных отрывных пузырей. При больших (критических) углах атаки на классических профилях отрыв потока создает не только дополнительное сопротивление, но и при определенных условиях приводит к резкому, скачкообразному снижению подъемной силы крыла. Поэтому устранение отрыва в этом случае является весьма актуальной задачей.

Данная глава посвящена экспериментальному исследованию возможности управления обтеканием модели прямого крыла с помощью точечного воздействия — локального вдува. Метод основан на, полученных в предыдущих исследованиях, данных о существовании трехмерной вихревой структуры течения внутри области срыва.

Результаты проведенных экспериментов, описанных в данной главе, были опубликованы в работе [122].

4.1. Условия проведения эксперимента.

Эксперименты были проведены в дозвуковой аэродинамической трубе МТ-324 на моделях крыльев малого № 1 и умеренного № 2 удлинения.

Каждая модель помещалась в рабочую часть и жестко закреплялась с помощью специального кронштейна к нижней поверхности рабочей части. Крепления крыла, кронштейн имели удобообтекаемый профиль и на поток существенного влияния не оказывали. Проводилось несколько серий экспериментов при разных скоростях набегающего потока с вдувом воздуха и без, в которых модели устанавливались от малых до критических углов атаки, тем самым изменяя режим обтекания от образования отрывного пузыря на верхней поверхности крыла до глобального срыва потока с передней кромки. Также изменялось местоположение отверстия на поверхности крыла и его геометрические размеры. Угол скольжения - Р = 0°.

Объектом исследований была структура течения до и после локального воздействия воздухом. Основными методами исследований картин течения была «саже-масляная» визуализация и метод шелковинок. Для получения количественных данных о структуре течения над крылом были проведены термоанемометрические и пневмометрические измерения.

4.2. Влияние локального воздействия при срывном режиме обтекания на крыле малого удлинения.

Выше уже отмечалось, что существуют методы устранения отрыва и присоединения потока, в которых используются турбулизаторы или вихрегенераторы. Эти устройства устанавливаются перед зоной отрыва и приводят к присоединению потока. Отличие метода локального вдува в том, что отверстие, через которое подается воздух, находится внутри области отрыва, тем самым влияние оказывается на его внутреннюю структуру. Особенно важным представляется понять, как такое воздействие повлияет на интегральные характеристики течения.

Подобные эксперименты необходимы для поиска новых принципов управления обтеканием, основанных на применении точечных источников возмущений, что энергетически выгодно, поскольку позволяет с минимальными затратами энергии добиться улучшения аэродинамических характеристик летательных аппаратов. Именно в этом направлении сейчас в мире разрабатываются перспективные способы управления обтеканием с помощью микроэлектронных механических систем (MEMS). Задача заключается в том, чтобы значительно увеличить несущие свойства крыла без применения сложных технических устройств, что особенно важно для малоразмерных беспилотных летательных аппаратов.

Первая серия экспериментов была посвящена изучению возможности управления срывным обтеканием крыла с помощью локального вдува воздуха на модели № 1.

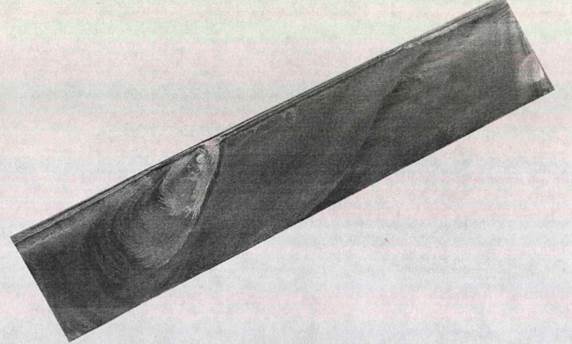
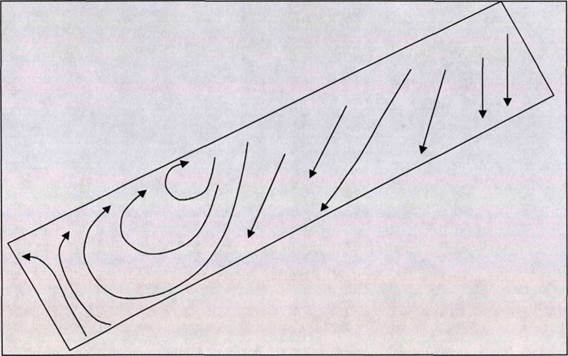
Для выхода на нужный режим обтекания модели крыла, при котором наблюдается возвратное течение и срыв потока, постепенно менялся угол атаки до достижения диапазона критических углов. На рис. 4.1 представлен, в данном случае, один из наиболее интересных результатов при таком режиме обтекания. Угол атаки был равным а — 21°. Скорость набегающего потока составляла и«, = 11,5 м/с. Re = 2,2 * 10⁵. Визуализация различными методами показала, что при таком режиме обтекания существует не только возвратное течение с парой крупномасштабных вихрей, но и существование застойной зоны, находящейся между передней кромкой и крупномасштабными вихрями (рис. 4.1). Направление потока - сверху вниз. Стоить отметить, что эти вихри образовались только на верхней половине крыла, в отличие от образовавшихся вихрей, представленных на рис. 3.1 (б-г).

Как уже отмечалось выше, для управления обтеканием локальное воздействие должно быть расположено внутри области срыва. Согласно этому, воздух подавался со скоростью в диапазоне 3-5 м/с через отверстие, расположенное за линией отрыва вниз по потоку. Также изменялся угол атаки а, скорость набегающего потока U», местоположения отверстия и его размеры. Наиболее характерные результаты представлены ниже.

В результате экспериментов было выявлено, что максимальный эффект от локального воздействия достигается, если отверстие расположено по оси

Дата добавления: 2015-05-08