На защиту выносятся 5 страница

5.3. Развитие возмущений в отрывном течении до и после локального воздействия.

Для более подробного изучения структуры обтекания в режиме при угле атаки а = 20° и скорости набегающего потока и«, — 19 м/с были проведены дополнительные исследования. Это тот случай когда эффект от локального воздействия максимален. Визуализация этого режима представлена выше (рис. 5.2 и рис. 5.3). В данных измерениях в качестве локального воздействия использовался только конический выступ.

Термоанемометрические измерения, выполненные вдоль хорды модели на 1/4 по размаху крыла (рис. 5.7, а), дали результаты, подтверждающие отрыв потока без локального воздействия и присоединенное течение при локальном воздействии. Профили средней скорости течения без локального воздействия, начиная с точки х/Ь=0,05, имеют отрывную форму (здесь х/Ь - продольная координата, отнесенная к хорде модели). В режиме обтекания с локальным воздействием профили средней скорости имеют форму, показывающую, что от передней до задней кромки модели крыла течение присоединенное.

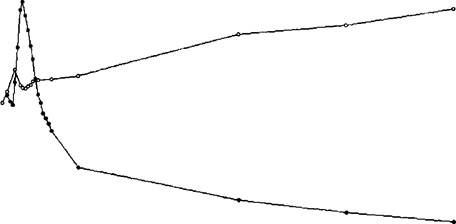
Была получена кривая нарастания пульсаций вдоль хорды крыла при обоих режимах обтекания. Изменение уровня возмущений вдоль линии равной средней скорости, составляющей 0,5 от скорости набегающего потока, что соответствует максимуму амплитуды пульсаций (рис. 5.7, б). При обоих режимах обтекания наблюдается пики амплитуды пульсаций, при ламинарно-турбулентном переходе, примерно в одной и той же области х/Ь=0,08-0,1 над моделью крыла. Частотные спектры пульсаций, см. ниже, подтверждают наличие ламинарно-турбулентного перехода. При срывном обтекании модели после завершения перехода уровень пульсаций уменьшается и далее снова начинает нарастать вниз по потоку. Максимальная амплитуда пульсаций в конце отрывной зоны превышает соответствующую величину, достигаемую при ламинарно-турбулентном

хЛ1=0.05

х/Ъ=0 09

х/Ъ=0.18

хЛ1=0.27

хЛ1=0.44

>(/11=0.62

1С0

£0

СО

ьи

СО

I»

^г ' ' О

О 10 20 30 0 10 20 30 0 10 20 30 0 10 20 30 0 10 20 30 0 10 20 30 0 10 20 30

и, м/с

Л'

О

О

а) профили средней скорости.

и'/ио, %

5 ______ I_____ I_____ I______ I_____ I______ I______ 1_____ I 0 01 02 03 04 05 ОБ 07 0В

х/Ь

б) кривые нарастания пульсаций.

Рис. 5.7. Средняя скорость и амплитуда пульсаций, о - течение без локального воздействия, • - течение с локальным воздействием.

переходе. В режиме обтекания с локальным воздействием после завершения перехода уровень пульсаций уменьшается вниз по потоку. Следует отметить, что в присоединенном режиме обтекания пик амплитуды пульсаций приходится над областью отрывного пузыря, существование которого было подтверждено визуализацией и измерениями статического давления на поверхности модели крыла — «полочка» на графике при х/Тг=0,1 (рис. 5.8). Эти измерения показали существенную разницу между уровнем разрежения над верхней поверхностью крыла потока при двух режимах обтекания.

Данный метод воздействия изменяет обтекание крыла и, возможно, позволит улучшить его аэродинамические характеристики. Таким образом, найден новый способ управления обтеканием. Применение этого метода для повышения несущих свойств крыла будет целью дальнейших исследований.

О 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 х/Ь

Рис. 5.8. Распределение статического давления на верхней поверхности

крыла.

По частотному составу пульсации при разных режимах обтекания различны (рис. 5.9, а и б). Переход от ламинарного к турбулентному течению происходит через развитие пакета волн неустойчивости, что наблюдается как в срывном режиме в области х/Ь=0,053-0,066 (частота волны 3,2 кГц), так и в присоединенном течении при х/Ь=0,067-0,075 (частота волны 8 кГц). Следует отметить появление и развитие субгармоники в обоих случаях, т.е. наблюдается субгармонический режим ламинарно-турбулентного перехода. При смещении вниз по потоку (до х/Ь=0,8) максимальная амплитуда

пульсаций в частотном спектре смещается в область низких частот, как при

/

срыве, так и при присоединенном течении.

Au(f)

x/h=0.800 x/h=0.440 x/h=0.110 x/h=0.089 x/h=0.075

0.8 0.7 0.6 05

0.4

x/h=0.066

^ч^^Л'^^_______________ x/h=0.058

\ x/h=0.053

0.2 0.1

i ~ -

V x/h=0.044

8 10 12 14 16 18

f, кГц

а) режим естественного обтекания.

x/h=0.800

x/h=0.092

x/h=0.075

Au(l)

0.5

0.3

0.2

x/h=0.070

₍yv_v

V

0.1

x/h=0.067

x/h=0.057

_i____ i__._ i____ ^{1 1}

6 10 12 14 16 18

f, кГц

б) течение с локальным воздействием.

Рис. 5.9. Частотный состав пульсаций в пограничном слое вдоль хорды

крыла.

5.4. Выводы к главе V.

1. Представлены результаты экспериментальных исследований обтекания модели прямого крыла, установленной под постоянным углом атаки, в режиме обтекания, при котором на поверхности крыла возникает срыв потока вблизи передней кромки или, при локальном воздействии, присоединенное течение с ламинарно-турбулентным переходом вблизи передней кромки крыла.

2. Установлено, что точечное локальное воздействие внутри области срыва позволяет преобразовать течение из срывного в присоединенное.

3. Получены данные визуализации и термоанемометрические измерения скорости и амплитуды пульсаций в обоих вариантах обтекания.

4. Найдено, что в результате искусственного присоединения значительно изменяется частота волны, развивающейся при переходе. Таким образом показано, что эта частота зависит не от частотного состава пульсаций в набегающем потоке, а от параметров пограничного слоя на поверхности крыла. Показано, что в обоих случаях развивается субгармоника основной волны, и её амплитуда становится больше амплитуды основной волны.

5. Обнаружен эффект увеличения амплитуды пульсаций вдоль хорды в срывном течении после ламинарно-турбулентного перехода за счет роста низко-частотных колебаний.

Глава VI. ИЗУЧЕНИЕ ВОЗМОЖНОСТЕЙ УПРАВЛЕНИЯ ОТРЫВОМ С ПОМОЩЬЮ ЛОКАЛЬНОГО ВОЗДЕЙСТВИЯ ПРИ РАЗЛИЧНЫХ УГЛАХ

СКОЛЬЖЕНИЯ.

Описанные выше эксперименты оставили открытым вопрос о возможности управления обтеканием крыла, установленном на разных углах скольжения, при срыве потока. Для решения этого вопроса были проведены экспериментальные исследования, описанные в данной главе. В качестве локального воздействия применялись выступы различной формы. Эта серия экспериментов также имела поисковый характер. Новизна работы заключалась в том, что локальное воздействие производилось за линией глобального отрыва вниз по потоку при разных углах скольжения крыла.

6.1. Условия проведения эксперимента.

Эксперименты были проведены в дозвуковой аэродинамической трубе МТ-324 на модели крыла умеренного удлинения № 6. Модель помещалась в рабочую часть и жестко закреплялась с помощью специального кронштейна к нижней поверхности рабочей части. Крепления крыла, кронштейн имели удобообтекаемый профиль и на поток существенного влияния не оказывали. Проводилось несколько серий экспериментов при разных углах скольжения крыла в срывном режиме обтекания с локальным воздействием и без него. Скорость набегающего потока оставалась постоянной и не изменялась в течение исследований. В качестве локального воздействия применялись выступы в форме конуса и ребра. Эти выступы устанавливались за линией отрыва вниз по потоку в различных местах.

Объектом исследований была структура течения до и после локального воздействия. Основными методами исследований картин течения была саже- масляная визуализация.

6.2. Трансформация отрывной зоны с изменением угла скольжения.

Первым этапом экспериментов стало изучение эволюции вихревых структур в области отрыва при изменении угла скольжения. Исследования были начаты с угла скольжения [3 = 0°. Срывной режим обтекания наблюдался при закритическом угле атаки а = 16° (рис. 6.1, а). Скорость набегающего потока составляла и» = 25 м/с и в дальнейшем это значение не изменялось. На крыле сформировалась пара крупномасштабных вихрей, вращающихся в противоположных направлениях, и появилось пристенное возвратное течение от задней кромки крыла в сторону передней. Вблизи передней кромки и по всему размаху крыла образовалась, так называемая, застойная зона, перед которой происходило растекание возвратного течения в левую и в правую сторону. Необходимо отметить, особенность данного профиля состоит в том, что фокусы крупномасштабных вихрей размазаны, и точно указать их местоположение не представляется возможным.

Увеличение угла скольжения крыла до Р = 15° существенно изменило картину обтекания (рис. 6.1, б). Полностью исчез один крупномасштабный вихрь. Второй вихрь остался, и стал четко виден фокус вихря. На большей части крыла наблюдалось возвратное течение.

При достижении угла скольжения (3 = 30° срывной режим начинался только со значения угла атаки а = 18°. При этом крупномасштабный вихрь сместился в центральную часть крыла, и область возвратного течения значительно уменьшилась (рис. 6.1, в).

При дальнейшем увеличении угла скольжения срыв потока с передней кромки исчезал, и на крыле наблюдалось присоединенное течение.

Таким образом, зная структуру обтекания крыла при различных углах скольжения, можно исследовать возможности управления.

Рис. 6.1. Процессы перестройки вихревого течения в зависимости от угла скольжения.

6.3. Влияние выступов на вихревую структуру обтекания.

На втором этапе экспериментов изучалась возможность управления структурой вихревого течения с помощью конических выступов и ребер в зависимости угла скольжения, как и в экспериментах на первом этапе.

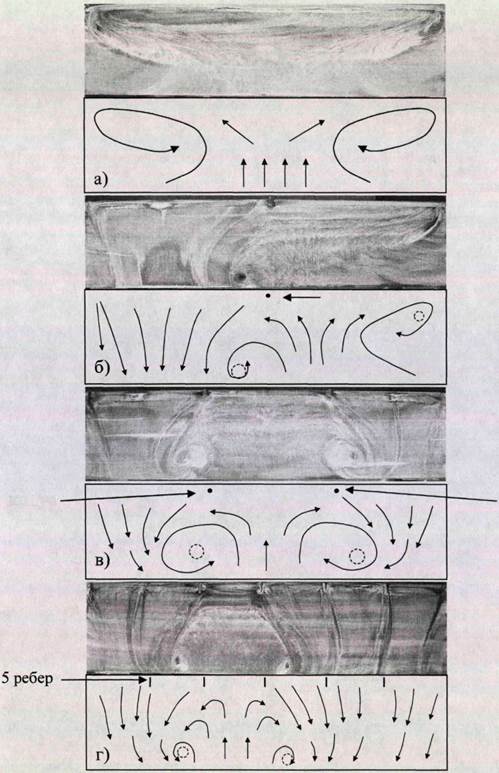
На рис. 6.2 приведены картины визуализации на поверхности модели с локальным воздействием при нулевом угле скольжения. Угол атаки составлял а = 16°, и скорость набегающего потока была равна 25 м/с, значение которой в последующих экспериментах не менялось. Один конический выступ, установленный на 1/2 части размаха крыла, позволил присоединить поток на половине поверхности крыла и, тем самым, значительно уменьшил область срыва (рис. 6.2, б). Высота и диаметр основания конуса были равны 20 мм и 8 мм соответственно. Расстояние от передней кромки составляло 12 мм. Затем было установлено два идентичных выше описанному по размерам конуса на 1/3 и 2/3 части по размаху крыла и на расстоянии 12 мм от передней кромки. В результате локального воздействия срывная область значительно уменьшилась в размерах (рис. 6.2, в).

Замена конусов на ребра дала тот же эффект в экспериментах описанных выше. Были получены идентичные картины течения. Длина одного ребра составляла 20 мм, высота- 4 мм и ширина- 3 мм. Расстояние от передней кромки до ребра было равно 4 мм. Ребра устанавливались в продольном направлении.

При установке 5 ребер на 1/6, 1/3, 1/2, 2/3 и 5/6 части размаха крыла осталась только одна срывная область (рис. 6.2, г).

Нужно отметить, что конусы выступали вверх из области отрыва, создавая тем самым турбулентный след, который мешал перетеканию потока из одной части крыла в другую, тем самым видоизменяя структуру обтекания в целом. Ребра, которые были полностью погружены внутрь отрывной области, мешали перетеканию вблизи передней кромки, что также видоизменяло структуру обтекания в целом.

При угле скольжения р = 15° максимально удалось присоединить поток с помощью только одного конуса, расположенного на 1/2 части по размаху крыла. Расстояние от передней кромки равнялось 14 мм. Высота конуса составляла 15 мм, диаметр основания- 10 мм. На правой части крыла было безотрывное обтекание, на левой - возвратное течение (рис. 6.3, б). Крупномасштабный вихрь сместился в центральную часть. Ребро, установленное также на 1/2 части по размаху крыла, дало тот же эффект (рис. 6.3, в). Расстояние до передней кромки составляло 7 мм. Высота равнялась 4 мм и длина- 22 мм.

Нужно отметить, что установка большого по размерам ребра, расположенного на 1/2 части размаха крыла, совсем не повлияла на вихревую структуру потока (рис. 6.3, г). Длина ребра составляла 73 мм и высота- 8 мм. Расстояние до передней кромки - 49 мм. Из этого следует, что влиять на структуру потока можно только вблизи передней кромки.

Затем был увеличен угол стреловидности до (3 = 30° и угол атаки до а = 18°. Максимальный эффект от локального воздействия в виде ребра наблюдался на 1/4 и на 1/6 части размаха крыла (рис. 6.4, б и в). В первом случае отрывную область удалось значительно уменьшить в размерах. Во втором получилось полностью присоединенное течение. В обоих случаях расстояние от передней кромки составляло 6 мм. Длина ребра равнялась 20 мм и высота - 4 мм.

Установка ребра на 1/2 части размаха крыла, также как при угле скольжения (3 = 15°, не повлияло на структуру обтекания (рис. 6.4, г). Расстояние до передней кромки было 63 мм. Длина составляла 82 мм, высота - 9 мм.

Рис. 6.2. Влияние локального воздействия на структуру вихревого течения

U. (3 = 0°

конус

конус

конус

при угле скольжения р = 0°. • - конус, | - ребро.

Р= 15°

Рис. 6.3. Влияние локального воздействия на структуру вихревого течения при угле скольжения р = 15°. • - конус, | - ребро.

и_о

р = 30^е

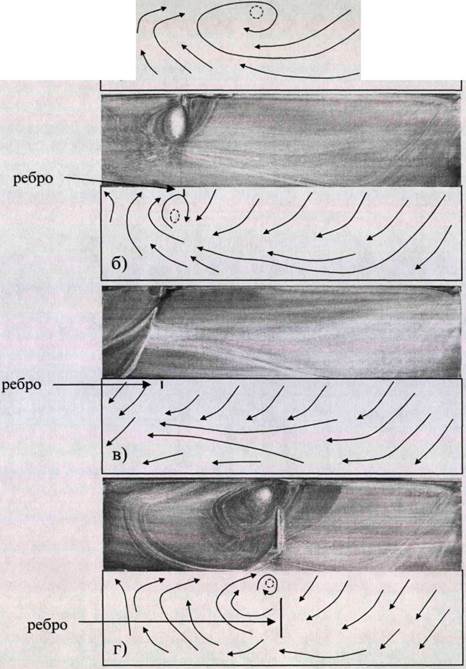Рис. 6.4. Влияние локального воздействия на структуру вихревого течения при угле скольжения [3 = 30°. • - конус, | - ребро.

6.4. Выводы к главе VI.

1. Экспериментально были изучены вихревые структуры, возникающие внутри области срыва на модели прямого крыла, и их зависимость от углов скольжения и атаки.

2. Проведены экспериментальные исследования обтекания модели крыла, установленной под разными углами скольжения, в которых изучались возможности управления обтеканием с помощью локального воздействия.

3. Обнаружено, что рёбра, как и канонические выступы, также значительно изменяют картину течения, вследствие того, что они препятствуют поперечным течениям в области отрыва вблизи передней кромки.

4. Найдены места на поверхности скользящего крыла, в которых ребра оказывают максимальное воздействие. Это область вблизи передней кромки модели вниз по потоку от фокуса вихря, в которой наблюдается возвратное течение.

ЗАКЛЮЧЕНИЕ.

В работе выполнен комплекс экспериментальных исследований отрывного обтекания моделей крыльев и возможностей управления отрывом с помощью локального воздействия с учетом таких факторов, как форма профиля, удлинение крыла, скорость набегающего потока, углы скольжения и атаки. Полученные сведения могут использоваться для решения практических задач по изучению и совершенствованию обтекания летательных аппаратов и для уточнения физических моделей наблюдаемых явлений.

Основные результаты работы заключаются в следующем:

Определена структура вихревого обтекания моделей крыльев при различных углах скольжения (в диапазоне от 0° до 45°) и атаки (в диапазоне от 0° до 21°). Показано влияние этих параметров на процессы перестройки течения вблизи поверхности моделей крыльев. Найдено, что увеличение угла скольжения приводит, в некоторых случаях, к устранению отрыва и присоединению потока. Определен критерий по удлинению крыла, при котором происходит деление и образование новых крупномасштабных вихревых пар.

• Используя полученные данные о картине отрывного обтекания, предложен новый метод локального воздействия на структуру течения. Показано, что преобразовать течение из срывного в присоединенное можно с помощью локального воздействия в одной точке на поверхности модели, причём эта точка находится внутри области срыва.

Показано, что в качестве локального воздействия можно использовать как точечный вдув воздуха, так и выступы в виде ребер или конусов. Продемонстрировано, что механизм воздействия во всех этих случаях имеет общую природу, вследствие того, что создается препятствие поперечным течениям в области отрыва, которое, в свою очередь, приводит к значительному изменению картины обтекания.

Установлено, что точечное локальное воздействие на модели крыла может влиять на срыв потока при всем его многообразии, вплоть до полного устранения отрыва, если заранее известна структура течения вблизи крыла. Тем самым этот метод может быть применен для управления обтеканием.

СПИСОК ЛИТЕРАТУРЫ.

1. Чжен П. Отрывные течения. // Т 1. М.: Мир, 1972. 300 с.

2. Шлихтинг Г. Теория пограничного слоя. // М.: Наука, Физматлит. 1969. 744 с.

3. Horton Н.Р. A semi-empirical theory for the growth and bursting of laminar separation bubbles.//Aeronaut. Research Council CP. 1967. No. 1073.

4. Жук В.И., Рыжов О.С. Свободное взаимодействие и устойчивость пограничного слоя в несжимаемой жидкости. // Докл. АН СССР. 1980.

, Т. 253(6). С.1326-1329.

5. Smith F.T. On the non-parallel flow stability of Blasius boundary layer. // Proc. Roy. Soc. London Sr. A. 1979. Vol. 366. P. 91-109.

6. Briley W.R. A numeral study of laminar separation bubble using the Navier- Stokes equations. //J. Fluid Mech. 1971. Vol. 47. P. 713-736.

7. Bestek H., Gruber K., Fasel H. Direct numerical simulation of unsteady separated boundary-layer flows over smooth backward-facing steps. // Physics of Separated Flows. Numerical, Experimental, and Theoretical Aspects / Ed. K. Gersten. Brauschweig: Vieweg, 1993. P. 73-80.

8. Bestek H., Gruber K., Fasel H. Self-exited unsteadiness of laminar separation bubbles caused by natural transition. // The Prediction and Exploitation of separated Flow / Royal Aeronautical Society. London, 1989. P. 14.1-14.16

9. Dallmann U., Herberg Т., Gebing H., Su W.H., Zhang H.Q. Flow field diagnostics: Topological flow changes and spatio-temporal flow structure. AIAA Paper N95-0791. 1995.

1 O.Pauley L.L., Moin P., Reynolds W.C. The structure of two-dimensional separation. // J. Fluid Mech. 1990. Vol. 220. P. 397-411.

ll.Tafti D.K., Vanka S.P. A numerical study of flow separation and reattachment on a blunt plate. // Phys. Fluids A. 1991. Vol. 3. P. 1749-1759.

12. Gaster M. The structure and behavior of separation bubbles. ARC R and M 3595. 1967.

13. Arena A.V., Mueller T.J. Laminar separation, transition, and turbulent reattachment near the leading edge of airfoils. // AIAA J. 1980. Vol. 18(7). P. 747-753.

14. Rannacher J., Untersuchung von geraden ebeden Fluge 1 gittern im kritischen Reynoldszahlbereich. // Kurzfassung in Maschinenbautechnik. 1969.

15. Gates E.M. Observation of transition on some axisymmetric bodies. // Laminar-Turbulent Transition. Eds. R. Epper, H. Fasel. Berlin: Springer­Verlag. 1980. P. 351-353.

16. Brendel M., Mueller T.J., Boundary-layer measurements on an airfoil at low Reynolds numbers. // J. Aircaft. 1988. Vol. 25. P. 612-617.

17. Довгаль A.B., Занин Б.Ю. Влияние турбулентности набегающего потока на развитие возмущений в течении с отрывом пограничного слоя. // Неустойчивость до- и сверхзвуковых течений. Под. ред. В.Я. Левченко; Ин-т теорет. и прикл. механики СО АН СССР. Новосибирск. 1982. С. 77-84.

18. Cousteix J., Pailhas G. Étude exploretore d'un prosessus de transition laminaire-turbulent au voisinage du decollement d'une couche laminare. // La Recherche Aérospatinale. 1979. № 3. P. 213-218.

19. Leblanc P., Blackweier R., Liebec R. Experimental results on separation on two airfoil at low Reynolds numbers. // 29th Aerospace Sciences Meeting. Reno. USA. 1991.

20. Бойко A.B., Довгаль A.B., Козлов В.В., Щербаков В.А. Неустойчивость и восприимчивость пограничного слоя в окрестности двумерных неоднородностей поверхности. // Изв.СО АН СССР. Сер. техн. наук. 1990. Вып. 1. С. 50-56.

21. Довгаль А.В., Козлов В.В. Устойчивость отрывного течения в двугранном угле. // Изв.СО АН СССР. Сер. техн. наук. 1984. Вып. 1(4). С. 47-51.

22. Masad J.A., Nayfeh А.Н. Stability of separating boundary layers. // Fourth Intern. Conf. of Fluid Mench.Vol. 1. Alexandria. 1992. P. 261-278.

23. Masad J.A., Nayfeh A.H. The influence of imperfections on the stability of subsonic boundary layers. // Instabilities and Turbulence in Engineering Flows / Eds. D.E. Ashpis et al. Netherlands: Kluwer. 1993. P. 65-82.

24. Бойко A.B., Довгаль A.B., Козлов В.В. и др. Отрыв ламинарного течения на двумерном препятствии в пограничном слое. Новосибирск, 19886. (Препринт / АН СССР. Сиб. отд-ние. Ин-т теорет. т прикл. механики; 7-88).

25. Левченко В.Я., Володин А.Г., Гапонов С.А. Характеристики устойчивости пограничных слоев. - Новосибирск: Наука. Сиб. отд-ние, 1975.

26. Герценштейн С.Я. О влиянии единичной шероховатости на возникновение турбулентности. // Изв.СО АН СССР. Механика жидкости и газа. 1966. № 2. С. 163-166.

27. Klebanoff P.S., Tidstrom K.D. Mechanism by which a two-dimensional roughness element induces boundary-layer transition. // Phys. Fluids. 1972. V. 15(7). P. 1173 - 1188.

28. Michalke A. On the inviscid instability of wall-bounded velocity profiles close to separation // Z. Flugwiss. Weltraumforsch. 1990. Vol. 14. P. 24­31.

29. Taghavi H., Wazzan A.R. Spatial stability of some Falkner - Skan profiles with reversed flow. // Phys. Fluids. 1974. Vol. 17(12). P. 2181-2183.

30. Nayfeh A.H., Ragab S.A., Masad J.A. Effect of a bugle on the subharmonic instability of boundary layers // Phys. Fluids A. 1990. Vol. 2(6). P.937-948.

31. Browand F.R. An experimental investigation of the instability of incompressible separated shear layer. // J. Fluid Mech. 1966. Vol. 26. P. 281-307.

32. Kachanov Yu., Levchenko V.Ya. The resonant interaction of disturbances at laminar-turbulent transition in a boundary layer. // J. Fluid Mech. 1984. Vol. 138. P. 209-247.

33. Miksad R.W. Experiment on the non-linear stages of free-shear layer transition. // J. Fluid Mech. 1972. Vol. 56. P. 695-719.

34.Sato H. Further investigation on the transition of two-dimensional separated layers at subsonic speed. // J. Phys. Soc. Japan. 1959. Vol. 14(12). P. 1797-1810.

35. Бойко A.B., Довгаль A.B., Козлов B.B. Нелинейные взаимодействия возмущений при переходе к турбулентности в зоне отрыва ламинарного пограничного слоя. // Изв. СО АН СССР. Сер. техн. наук. 1988а. Вып. 5(18). С. 44-49.

36. Качанов Ю.С., Козлов В.В., Левченко В.Я. Эксперименты по нелинейному взаимодействию волн в пограничном слое. Новосибирск. 19786. (Препринт / АН СССР. Сиб. отделение. Ин-т теорет. и прикл. механики; 16-18).

37. Miksad R.W., Jones F.L., Powers E.J. Measurements of nonlinear interactions during natural transition of a symmetric wake. // Phys. Fluids. 1983. Vol.26. P. 1402-1409.

38.Sato H. An experimental study of non-linear interaction of velocity fluctuations in the transition region of a two-dimensional wake. // J. Fluid Mech. 1970. Vol. 44. P. 741-765. 39.Kiya M. Separation bubbles. // Theoretical and Applied Mechanics / Eds. P.Germain, M.Piau, D.Caillerie. Elseiver Sci. Pub. B.V., 1989. P. 173-191.

40. Hasan M.A.Z. The flow over a backward-facing step under controlled perturbation: laminar separation. // J. Fluid Mech. 1992. Vol. 238. P. 73-96.

41. Roos F.W., Kegelman J.T. Control of coherent structures in reattaching laminar and turbulent shear layers. // AIAA J. 1986. Vol. 24. P. 1956-1963.

42.Sigurdson L.W., Roshko A. The structure and control of a turbulent reattaching flow. // Turbulence Management and Relaminarization / Eds. H.W. Liepmann, R. Narasimha. Springer-Verlag. 1988. P. 497-514.

43. Kiya M., Shimizu M., Mochizuki O., Ido Y., Tezuka H. Active forcing of an axisymmetric leading-edge turbulent separation bubble. // AIAA Pap. No. 93-3245. 1993.

44. Hammond D.A., Redekopp L.G. Local and global instability properties of separation bubbles. // Eur. J. Mech., B/Fluids. 1998. Vol. 17(2). P. 145-164.

45. Bogucki D.J., Redekopp L.G. A mechanism for sediment resuspension by internal solitary waves. // Geophysical Research Letters. 1999. Vol. 26(9). P. 1317-1320.

46. Hein S., Theofilis V., Dallmann U. Unsteadiness and three-dimensionality of steady two-dimensional laminar separation bubbles as result of linear instability mechanisms. // DLR IB. Goettingen. 1998. No. 223-98 A 39.

47. Choi D.H., Kang D.J. Calculation of separation bubbles using a partially parabolized Navier-Stokes procedure. //AIAA J. 1991. Vol. 29(8). P. 1267.

48. Crimi P., Reeves B.L. Analysis of leading-edge separation bubbles on airfoils. // AIAA J. 1976. Vol. 14. P. 1548-1555.

49. Vatsa V.N., Carter J.E. Analysis of airfoil leading-edge separation bubbles. //AIAA J. 1984. Vol. 22. P. 1697-1704.

50. Dini P., Maughmer M.D. A locally interactive laminar separation bubble model. // AIAA Paper № 90-0570. 1990.

51. Dini P., Selig M.S., Maughmer M.D. Simplified linear stability transition prediction method for separated boundary layers. // AIAA J. 1992. Vol. 30. P.1953-1961.

Дата добавления: 2015-05-08