
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Энергетический подход к взаимодействию
|
|
|
|
Электрическая энергия системы зарядов.
Часть 1
Ответы письменной работы по математике
| № задания | Ответ |
| Б1 | В |
| Б2 | С |
| Б3 | В |
| Б4 | А |
| Б5 | D |
| Б6 | В |
| Б7 | Е |
| Б8 | В |
| Б9 | A |
| Б10 | С |
| Б11 | 
|
| Б12 | 10 ч и 15 ч. |
| Б13 | 24 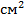 и и
 см. см.
|
| Б14 | 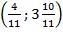 , (1; 2) , (1; 2)
|
Часть 2
| № задания | Ответ |
| П15 | 378 см2 |
| П16 | 50 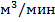
|
| П17 | 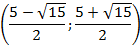
|
| П18 | 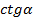
|
1.Рассмотрим систему, состоящую из двух точечных зарядов 1 и 2. Найдем алгебраическую сумму элементарных работ сил F1 и F2, с которыми эти заряды взаимодействуют. Пусть в некоторой К-системе отсчета за время dt заряды совершили перемещение dl1 и dl2. Тогда работа этих сил
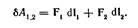
Учитывая, что F2 = -F1 (по третьему закону Ньютона), перепишем предыдущее выражение:
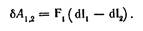
Величина в скобках – это перемещение заряда 1 относительно заряда 2. Точнее, это есть перемещение заряда 1 в К'-системе может быть представленно как перемещение dl2 К'-системы плюс перемещение dl1’заряда 1 относительно этой К'-системы: dl1 = dl2 + dl1’. Отсюда dl1 - dl2 = dl1’ и
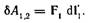
Итак, сумма элементарных работ в произвольной К-системе отсчета всегда равно элементарной работе, которую совершает сила, действубщая на один заряд, в системе отсчета, где другой заряд покоится. Иначе говоря, работа не зависит от выбора исходной К-системы отсчета.
Сила F1, действующая на заряд 1 со стороны заряда 2, консервативная (как сила центральная). Поэтому работа данной силы на перемещении dl1’ может быть представленна как убыль потенциальной энергии заряда 1 в поле заряда 2 или как убыль потенциальной энергии взаимодействия этой пары зарядов:
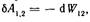
Где W12 – величина, зависящая только от расстояния между данными зарядами.
2. Теперь перейдем к системе из трех точечных зарядов. Работа, которую совершают все силы взаимодействия при элементарных перемещениях всех зарядов, может быть представлена как сумма работ всех трех пар взаимодействий, т.е. 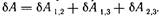 . Но для каждой пары взаимодействий, как только что было показано,
. Но для каждой пары взаимодействий, как только что было показано, 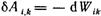 по этому
по этому
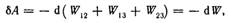
Где W– энергия взаимодействия данной системы зарядов.
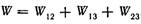 .
.
Каждое слагаемое этой системы зависит от расстояния между соответствующими зарядами, поэтому энергия W данной системы зарядов есть функция её конфигурации.
Это справедливо для любого числа зарядов. Значит, можно утверждать, что каждой конфигурации произвольной системы зарядов присуще свое значение энергии W, и работа всех сил взаимодействия при изменении этой конфигурации равна убыли W:
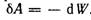 (4.1)
(4.1)
Энергия взаимодействия. Рассмотрим систему из трех точечных зарядов, для которой
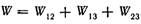 .Представим каждое слагаемое в виде:
.Представим каждое слагаемое в виде: 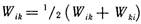 , поскольку
, поскольку  тогда
тогда 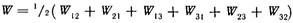 сгруппируем члены с одинаковыми первыми индексами
сгруппируем члены с одинаковыми первыми индексами
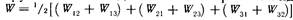
Каждая сумма в круглых скобках – это энергия Wi взаимодействия i – го заряда с остальными зарядами. Поэтому последнее выражение можно переписать так: 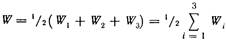
Данное выражение верно для любого количества зарядов. Итак, энергия взаимодействия системы точечных зарядов 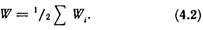
Зная, что 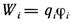 где
где 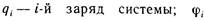 - потенциал, создаваемый всеми остальными зарядами в месте нахождения i – го заряда, получим выражение
- потенциал, создаваемый всеми остальными зарядами в месте нахождения i – го заряда, получим выражение 
|
|
|
|
|
Дата добавления: 2015-05-08; Просмотров: 288; Нарушение авторских прав?; Мы поможем в написании вашей работы!