Энергия электрического поля

О локализации энергии.Формула (4.4) определяет электрическую энергию W любой системы через заряды и потенциалы. Но энергию W можно выражить также и через величину, характеризующую само электрическое поле,- через напряженность Е. Убедимся в этом на примере плоского конденсатора, пренебрегая искажением поля у краев пластин(краевым эффектом). Подстановка в формулу 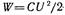выражения 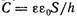дает

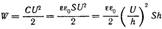
А поскольку 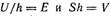(объем между обкладками конденсатора), то

Полученная формула справедлива для однородного поля, заполняющего объем V.

В случае неоднородного поля энергия W для изотропных диэлектриков определяется формулой

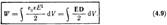
Подынтегральное выражение в этом уравнении имеет смысл энергии, заключенной в объем dV. Это подводит нас к физический идее о локализации энергии в самом поле. Данное предположение нашло опытное подтверждение в области переменных во времени полей. Именно переменные поля могут существовать независимо от возбудивших их электрических зарядов и распространяться в пространстве в виде электромагнитных волн. И опыт показывает, что электромагнитные волны переносят энергию, таким образом носителем энергии является само поле.

Из формулы(4.8 и 4.9) следует, что электрическая энергия распределена в пространстве с объемной плотностью

Заметим, эта формула справедлива в случае изотропного диэлектрика, для которого выполняется соотношение .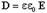

Для анизотропных диэлектриковдело обстоит сложнее.

Еще об обосновании формулы (4.9). Энергия уединеного заряженного проводника, как известно, есть 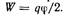Покахем, что это так, исходя иэ идеи о локализации энергии в поле.Рассмотрим произврльный положительно заряженный проводник. Выделим мысленно бесконечного малого сечения трубку, ограниченную линиями вектора Е (рис4.2) и вней воэьмем элементарный объем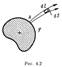

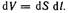Вэтом объеме закдючена энергия

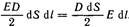
Теперь найдем энергию, локализованную во всей выделенной нами трубке. Для этого проинтегрируем последнее выражение, учитывая что произведение 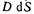одинаково во всех сечениях трубки, и поэтому его можно вынести за знак интеграла:

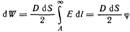
где А-начало трубки.

Остается сделать последний шаг –проинтегрировать полученное выражение во всех трубках, и мы найдем энергию, локализованную во всем поле. Принимая во внимание, что потенциал 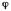одинаков у торцов всех трубок (они ведь начинаются на поверхности проводника), запишем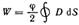

что и требовалось доказать.

Дата добавления: 2015-05-08