Оптимальная стратегия планирования дефицита

с его покрытием при очередной поставке

(без учета временной стоимости денег)

Рассматриваем суммарные годовые потери как функцию F (T, γ) двух переменных Т и γ (T>0, 0£ γ £1):

F(T, γ) = C₀/T + [ C_h·(1- γ)² + C_B·× γ ²] ·D·T/2

ЗАМЕЧАНИЯ 1.

¨ Отметим, что в граничной ситуации, когда γ = 0 (т.е. когда заведомо или априори дефицит не планируется) как легко видеть, параметры оптимальной стратегии будут определяться формулами Уилсона.

¨ Аналогично в другой граничной ситуации, когда γ = 1 (т.е. когда заведомо планируются поставки именно такого размера, который только покрывает дефицит), параметры оптимальной стратегии в невырожденном случае C_B >0 также будут определяться формалами Уилсона, но с учетом следующей особенности. А именно, - «роль» издержек хранения в такой ситуации будут «исполнять» уже издержки дефицита C_B, т.е. для оптимальных параметров при априори заданном значении γ = 1 получаем

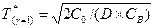
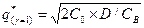
Вернемся к решению задачи минимизации суммарных потерь, представленных функцией F(T, γ).

Необходимое условие экстремума (T>0, 0£ γ £1):

∂F /∂ T = 0 C_h· (1- γ)² + C_B·γ² - 2C₀/(D·T²)= 0

∂F / ∂γ = 0 (C_h+C_B) · γ = C_h

ЗАМЕЧАНИЯ 2. Для невырожденного случая, когда C_h>0 и C_B >0 обратим внимание на следующее.

¨ Решение приведенной системы уравнений действительно дает именно точку минимума для F(T, γ) в интересующей нас области T>0, 0£ γ £1 (убедитесь в этом самостоятельно);

¨ Величина [ F (T, γ) – C₀/T)] при фиксированном Т представляет суммарные издержки хранения и дефицита, обусловленные именно планируемым балансом между t₁ и t₂ на Т.

Таким образом можно отметить следующее.

УТВЕРЖДЕНИЕ.

Для стратегии планирования дефицита (в невырожденном случае, когда C_h > 0 и C_B >0) при любом фиксированном Т>0 баланс длительностей интервалов наличия запасов t₁ и дефицита t₂ в рамках интервала повторного заказа зависит только от тарифов издержек С_h и С_В. При этом оптимальный такой баланс, при котором издержки при фиксированном Т будут минимальными, достигается, если

γ* = С_h/(C_h + C_B),

Дата добавления: 2015-05-08