Величина суммарных годовых затрат

Указанная величина для анализируемой модели определяется выражением:

,

причем для любого фиксированного Т = T₀ имеем: q_i = T₀ · D_i .

ЗАМЕЧАНИЕ. Учет стоимости продукции по каждому виду i -товара даст дополнительное слагаемое , не зависящее ни от q_i, ни от Т, а следовательно, не влияющее на точку минимума интересующей нас функции.

Введем дополнительно обозначения, которые помогут в удобном виде формализовать задачу нахождения оптимальной стратегии применительно к интересующей нас многономенклатурной модели управления запасами. А именно, пусть:

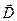=(D₁,D₂,…,D_N) – вектор потребления i -товаров;

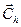=(C_h1,C_h2,…,C_hN) – вектор затрат на их хранение;

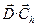- скалярное произведение этих векторов (напомним, что это – число, которое ищут по формуле 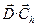= D₁× C_h1+ D₂× C_h2+ …+ D_N× C_hN).

ЗАДАЧА НАХОЖДЕНИЯ ОПТИМАЛЬНОЙ СТРАТЕГИИ

Соответствующая задача теперь может быть рассмотрена как задача минимизации суммарных затрат, представленных функцией С_Г(Т₀) переменной Т₀:

С_Г(Т₀) =

ЗАМЕЧАНИЯ.

1) Задача свелась к аналогичной задаче для базовой модели управления запасами, что позволяет легко найти основные параметры оптимальной стратегии. А именно, сначала находим оптимальное значение интервала Т₀* повторного заказа, затем (с учетом равенств q*_i = D_i∙Т₀*) находим оптимальный размер заказа q*_i по каждому i -товару.

2) Первое слагаемое в правой части представленного выражения (как функция переменной Т₀) представляет собой гиперболу, а второе слагаемое – линейную функцию. При этом легко видеть, что точка минимума существует.

3) Условие ∂С_Г/∂T₀ = 0 позволяет найти соответствующее единственное оптимальное значение длительности периода времени между общими поставками для рассматриваемой задачи минимизации общих годовых затрат, а затем и другие требуемые параметры оптимальной стратегии. Однако, указанные параметры проще получать, на основе соответствующей модификации приведенных в главе 2 формул Уилсона. Приведем соответствующие формулы.

ИНТЕРВАЛ ПОВТОРНОГО ЗАКАЗА (общий)

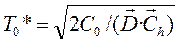(в годах).

Подчеркнем, что в случае когда поставки по каждому i-товару организуются независимо друг от друга, то соответствующий оптимальный интервал повторного заказа для i-товара равен . Сравнивая это выражение для Т_i^* c приведенным выше выражением для Т₀^* легко видеть, что применительно к многономенклатурной модели с общими поставками интервал повторного заказа становится (при сохранении накладных расходов на поставку) более «коротким»: Т₀*<Т_i*, т.к. С_hi ∙ D_i < .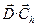

ЭКОНОМИЧНЫЙ РАЗМЕР ЗАКАЗА (i-товара).

,

Приведем пример использования соответствующих формул при управлении запасами.

Дата добавления: 2015-05-08