С учетом временной структуры процентных ставок. Для удобства записи соответствующей оптимизационной задачи введем, дополнительно, следующие обозначения

ПАРАМЕТРЫ ОПТИМАЛЬНОЙ СТРАТЕГИИ УПРАВЛЕНИЯ

Для удобства записи соответствующей оптимизационной задачи введем, дополнительно, следующие обозначения. Пусть

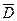· = (D₁, D₂ , …, D_N) – вектор годового потребления i -товаров;

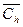· = (C_h1, C_h2, …, C_hN) – вектор соответствующих годовых затрат на хранение для единиц i -товаров;

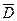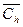· × - скалярное произведение векторов 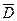и ;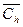

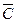· _п = (C_п1, C_п2, …, C_пN) – вектор стоимостей единиц i -товаров;

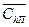· – вектор, равный сумме вектора 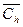и вектора r_З× 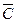_п;

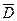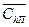· × - скалярное произведение векторов 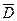и ;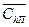

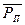· = (Р _п1, Р _п2, …, Р _пN) – вектор прибылей для единиц i -товаров;

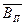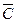· = _п+ 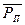– вектор выручки для единиц i -товаров;

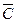· _оп= (C _{оп 1} , C_{оп 2} , …, C _{оп N}) – вектор соответствующих издержек доставки для единиц i -товаров;

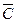· _опп - вектор, равный сумме вектора 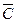_опи вектора 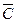_п;

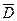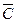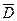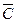· × _опп – скалярное произведение векторов и _опп.

Вернемся к анализу интересующей нас целевой функции F = F(Т_об ) в рамках рассматриваемой задачи максимизации интенсивности потока доходов для соответствующей системы управления запасами. Используя введенные обозначения перепишем (с учетом равенств Т_об = q_i /D_i ) эту функцию в следующем более компактном виде

F₀ (Т_об) = 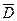× 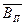– (1 + r T_об /2)[ 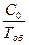+ 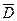× 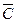_опп + × × ]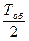

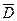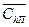Упорядочивая слагаемые по степеням Т_об, домножая при этом для удобства на 2, причем опуская слагаемые, которые не зависят от Т_об ,и меняя знак целевой функции на противоположный, перепишем задачу оптимизации в виде

[ 2 C₀ / Т_об + Т_об (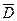 × 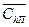)] + Т_об × r ×( 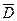× 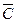_опп)+ Т²_об × 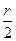×( ×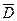 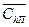) ® min.

Анализируя последнее выражение легко видеть, что в этой записи оно вполне аналогично (с учетом замены 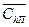на 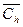) выражению для целевой функции применительно к рассмотренной в главе 7 модификации модели с учетом временной стоимости денег. Следовательно, все выводы, сделанные ранее в главе 7, относятся (с учетом указанной замены) и к анализируемому здесь случаю, когда помимо учета временной стоимости денег требуется учитывать и потери, обусловливаемые «замороженными» в запасах денежными средствами. А именно, отметим следующее.

1. В частности, первое слагаемое (специально выделенное и взятое в квадратные скобки), рассматриваемое как функция переменного Т_об в области Т_об > 0, имеет единственную точку минимума Т_об⁰ (напомним, что для такой точки справедливо равенство Т_об⁰ 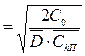, – см. приведенное выше сравнение для случая r = 0). Применительно к Т_об⁰ будут иметь место рекомендации, относящиеся к соответствующей модели, но без учета временной структуры процентных ставок и, соответственно, без учета временной стоимости денег.

2. Точка минимума (обозначим ее через Т_об^*) для функции F(Т_об) окажется расположенной в интервале (0; Т_об⁰), т.е. левее рекомендуемой при традиционном подходе точки Т_об⁰ применительно к аналогичной модели, когда временная структура процентных ставок не учитывается. Другими словами, оптимальное значение Т_об^* длительности периода времени между общими поставками (с учетом издержек «замороженных» в запасах денежных средств, а также с учетом временной стоимости денег) с всегда будет меньшим, чем дадут традиционные рекомендации, т.е. всегда в условиях рынка, когда необходимо учитывать соответствующие процентные ставки, выполняется неравенство

Т_об^* < Т_об⁰.

3. При этом, естественно, и для значений оптимальных размеров i -заказов q_i^* в поставляемой партии также выполняются неравенства

q_i^* < q_i⁰,

где q_i⁰ - рекомендуемые (но без учета временной стоимости денег) размеры i -заказов в партии общей поставки применительно к рассматриваемой модификации модели. Насколько велико соответствующее расхождение для этих основных параметров стратегии управления запасами и какие возможности для повышения эффективности системы дает учет временной стоимости денег можно будет увидеть из дальнейшего анализа.

4. Параметры, характеризующие оптимальную стратегию управления запасами применительно к анализируемому здесь случаю, когда помимо учета временной стоимости денег требуется учитывать и потери, обусловливаемые «замороженными» в запасах денежными средствами можно находить по представленному в главе 7 алгоритму. А именно, оптимальная величина длительности Т_об^* периода времени между общими поставками и оптимальные размеры i -заказов q_i^*, максимизирующие интенсивность потока доходов для рассматриваемой модификации модели управления запасами находятся по формулам

Т_об^* = Т_об⁰ / z₀

q_i^* = Т_об^* × D_i,

где

,

.

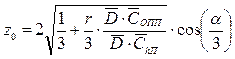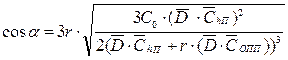ЗАМЕЧАНИЕ 1. Обратим внимание на следующий факт. Анализ полученных результатов для оптимальной стратегии управления запасами показывает, что в рамках рассматриваемой модели исследуемые параметры (оптимальная длительность периода времени Т_об^* между общими поставками и оптимальные размеры i -заказов q_i^* в партиях поставок) не зависят, как и для модификации модели в главе 7, от показателей Р_Пi , характеризующих прибыль на единицу i -товара.

ЗАМЕЧАНИЕ 2. Кстати, обратим внимание на то, что полученное выше выражение для функции F = F(Т_об ) дает возможность получать соответствующие формулы, по которым следует оценивать различные годовые издержки или потери применительно к рассматриваемой модели для ситуации, когда учитывается временная стоимость денег (в отличие от традиционных рекомендаций, при которых процентные ставки не учитываются). А именно, в частности, приведем их применительно к следующим показателям.

1. Для накладных расходов на общие поставки анализируемой группы товаров за год –

(1+ r×Т_об/2)×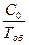

(а не С₀ /Т_об, как это принято в традиционных рекомендациях).

2. Для годовых издержек хранения по i -товарам –

(1+ r×Т_об/2)× 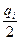× C_hi

(а не 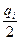× C_hi, как это принято в традиционных рекомендациях).

3. Для суммарных годовых издержек хранения по всем видам товаров –

(1+ r×Т_об/2)×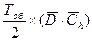

(а не 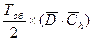, как это принято в традиционных рекомендациях).

4. Для годовых потерь из-за «замороженных» денежных средств в i-товарах –

(1+ r×Т_об/2)× r_З× 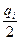× C_Пi

(а не r_З× 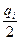× C_Пi, как это принято в традиционных рекомендациях).

5. Для суммарных годовых потерь из-за «замороженных» денежных средств по всем видам товаров –

(1+ r×Т_об/2)× r_З×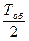

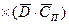
(а не r_З× 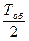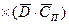, как это принято в традиционных рекомендациях).

6. Для среднегодовых затрат на содержание запасов по i -товарам –

(1+ r×Т_об/2)× 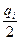× C_Пi

(а не 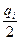× C_Пi, как это принято в традиционных рекомендациях).

7. Для суммарных среднегодовых затрат на содержание запасов по всем видам товаров –

(1+ r×Т_об/2) ×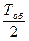

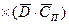
(а не 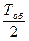× 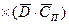, как это принято в традиционных рекомендациях).

ПРИМЕР 8.2. Для иллюстрации соответствующих процедур нахождения интересующих нас параметров оптимальной многономенклатурной стратегии управления запасами с общими поставками в рамках рассматриваемой модели с учетом временной стоимости денег, а также для иллюстрации отклонений основных показателей такой оптимальной стратегии по сравнению с рекомендациями традиционного подхода (без учета временной структуры процентных ставок) рассмотрим условную ситуацию предыдущего примера 8.1 с тремя видами продуктов. А именно, параметры модели соответствуют классическому примеру из книги [Дж. Букан, Э. Кенигсберг Научное управление запасами. – М.: Наука, 1967]. Для наглядности они представлены в следующей таблице.

Табл. 8.2

Показатели, характеризующие запасы трех видов продукции

Продукт
Годовое потребление Di	D1 = 12000	D2 = 25000	D3 = 6000
Издержки хранения Сhi	Ch1 = 0,6	Ch2 = 0,4	Ch3 = 1,2
Стоимость ед. товара Спi	Cп1 = 3	Cп2 = 2	Cп3 = 6

Дополнительно, для удобства дальнейшего сравнения результатов с аналогичными, но уже для классической модели без учета временной стоимости денег, как и ранее, полагаем C_опi = 0 (например, соответствующие издержки уже включены в стоимость товара). Кроме того, пусть при общих поставках накладные расходы на одну поставку составляют С₀ = 40 (у.е.). Также для определенности считаем, что Р_пi / C_пi = 0,5 (для всех видов продуктов). Наконец, принимаем, что годовая ставка наращения составляет 20%, т.е. r = 0,2, а соответствующие годовые потери для «замороженных» в запасах денежных средств также составляют 20%, т.е. r_З = 0,2.

Найдем параметры оптимальной стратегии управления запасами при общих поставках этих товаров с учетом временной структуры процентных ставок и сравним их с полученными в примере 8.1.

РЕШЕНИЕ. Прежде всего отметим, что в рамках рассматриваемого примера имеем:

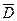· = (12000; 25000; 6000), 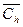= (0,6; 0,4; 1,2), так что ( 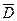× 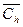) = 24400, (т.к. 24400 = 12000×0,6 + 25000×0,4 + 6000×1,2);

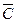· _п = (3; 2; 6), так что 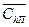= (1,2; 0,8; 2,4);

· поскольку 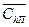=2× 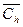, то ( 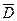× 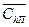) = 48800;

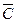· _опп = 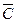_п = (3; 2; 6), т.к. С _опi = 0;

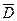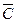· × _опп = 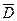× 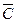_п = 122000 (=12000×3 + 25000×2 + 6000×6).

Для нахождения оптимальной стратегии в данной ситуации с учетом временной стоимости денег, предварительно находим значение соответствующего cosa:

,

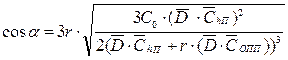
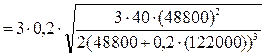т.е. cosa = 0,011452.

Затем, переходя к 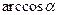(как видим, для данной ситуации он, практически, соответствует 90°) находим значение 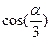= 0,867. После этого определяем значение показателя z₀:

,

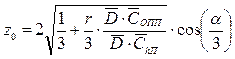
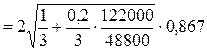т.е. z₀ = 1,2247.

Определив значение z₀ = 1,2247, переходим к анализу основных параметров оптимальной стратегии управления запасами в рамках рассматриваемого примера. А именно, соответствующее оптимальное значение Т_об ^* периода времени между общими поставками с учетом временной стоимости денег для рассматриваемого случая составляет (с учетом того, что Т_об⁰ = 0,04049, - см. пример 8.1):

Т_об ^* = Т_об ⁰ / z₀ = 0,04049 / 1,2247 = 0,03306.

Соответственно, в оптимальном случае с учетом временной стоимости денег при общих поставках этих товаров (после округления) имеем:

· объемы товаров в заказе –

q₁⁰ = 397, q₂⁰ = 826, q₃⁰ = 198;

· издержки хранения Х_i⁰ (годовые) по видам i- товаров –

Х₁⁰ = 119, Х₂⁰ = 165, Х₃⁰ = 119 (у.е.);

· среднегодовые стоимости запасов по видам i- товаров –

C₃₁ = 594; C₃₂ = 826; C₃₃ = 594.

· накладные расходы на общие поставки по анализируемой группе товаров за год составят 1210(у.е.).

· средние годовые потери из-за «замороженных» в запасах суммах – 403 (у.е.).

Теперь напомним параметры оптимальной стратегии для случая традиционного подхода, когда временная стоимость денег не учитывается. В этом случае, как было показано в примере 8.1, получилось Т_об⁰ = 0,04049 (или @ 15 дней). Соответственно такой рекомендации при общих поставках этих товаров было найдено (после округления):

· объемы i-товаров в заказе –

q₁⁰ = 485, q₂⁰ = 1012, q₃⁰ = 242;

· годовые издержки хранения (обозначим их через Х_i⁰) по видам i- товаров –

Х₁⁰ = 146, Х₂⁰ = 202, Х₃⁰ = 146 (у.е.);

· среднегодовые стоимости запасов по видам i- товаров –

C₃₁ = 727; C₃₂ = 1012; C₃₃ = 727;

· накладные расходы на поставки товаров за год составят 988 (у.е.);

· средние годовые потери из-за «замороженных» в запасах суммах – 493 (у.е.).

Как видим, для модифицированной модели при оптимальном управлении запасами с учетом временной стоимости денег (сравните с исходной моделью примера 8.1) имеем:

издержки, обусловливаемые накладными расходами на поставки за год составят 1210 (вместо 988);

суммарные годовые издержки хранения по всем трем видам продуктов составят 403 (вместо 494);

средняя годовая суммарная стоимость запасов по всем трем видам продуктов - 2014 (вместо 2466);

среднегодовые потери из-за «замороженных» в продуктах денежных суммах – 403 (вместо 493).

Итак, если не учитывать временную структуру процентных ставок, то рекомендуемое в рамках традиционного подхода значение периода времени между общими поставками в рамках рассматриваемого примера равняется Т_об ⁰ = 0,04049 (@ 15 дней). Учет временной стоимости издержек/доходов приводит соответственно к оптимальному значению этого показателя, которое в нашем примере составляет Т_об ^* = 0,03306 (@ 12 дней). Как видим, отклонение для периода времени между общими поставками партий заказов от оптимального с учетом временной стоимости денег соответствует в данной ситуации ошибке порядка 25%. Понятно, что такая ошибка может привести к существенному изменению стратегии управления запасами и, кроме того, может значительно отразиться на показателе эффективности работы системы. В частности, оценим соответствующее отклонение показателя интенсивности доходов в рамках рассматриваемого примера для интересующих нас двух случаев:

1) при T = T_об ^* = 0,03306 (стратегия реализуется с учетом временной стоимости издержек/доходов);

2) при T = Т_об ⁰ = 0,04049 (стратегия реализуется по рекомендациям без учета временной стоимости издержек/доходов).

Случай 1. При стратегии, использующей показатели T_об ^* и q_i ^* для интенсивности доходов F_max (годовой) имеем:

F_max = 183 – (1+ 0,2×0,03306 / 2)×(0,04 / 0,0341 +122+ 48,8×0,03306 / 2) = 58,6

(тыс. у.е./год)

Случай 2. При стратегии, использующей соответственно показатели Т_об ⁰ и q_i ⁰ для интенсивности доходов F⁰ (годовой) имеем:

F⁰ = 183 – (1+ 0,2×0,04049/2)×(0,04/0,04049+122+48,8×0,04049/2)= 58,51

(тыс. у.е./год)

Как видим, разность F_max – F⁰ в интенсивности доходов (годовой) для этих случаев по анализируемым видам товаров снова имеет порядок 90 у.е. (за год) несмотря на некоторое увеличение общих издержек. Напомним, что в реальных системах управления запасами соответствующий перечень номенклатуры товаров может измеряться сотнями и даже тысячами наименований. Кроме того, при уменьшении длительности интервала времени между общими поставками товаров соотвественно уменьшается и объем страхового запаса по этим товарам, а следовательно и «замороженные» в таком запасе вложенные в товар деньги. Поэтому суммарный показатель возможного повышения эффективности системы за счет учета временной структуры процентных ставок по всей группе товаров может оказаться весьма существенным.

Дата добавления: 2015-05-08