Оптимальные параметры для стратегии

ПЛАНИРОВАНИЯ ДЕФИЦИТА

Избавляясь от q_i в выражении для F (с учетом равенств Т = q_i /D_i), после простых преобразований (они здесь опускаются из-за ограниченности объема работы) целевая функция F как функция переменных T и γ_i легко приводится к следующему виду

F = SD_i × (Р_Пi – С_0Пi) – С₀ × 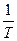– TS 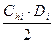∙ (1 –γ_i)² – TS 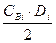∙γ_i ²

– T S(C_Пi + P_Пi) × D_i ∙ (1 – γ_i)² ×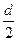

(*)

Далее, опуская первое слагаемое, которое не зависит от параметров стратегии управления запасами, меняя знак целевой функции на противоположный и умножая при этом для удобства записи на 2, перепишем задачу оптимизации в виде

f ® min,

где функция f определяется равенством

f = 2 C₀ / T + TSD_i ×(1 – γ_i)² ∙[ C_hi + d(C_Пi+Р_Пi) ] + TSD_i × γ_i ²∙ С_Вi.

При этом значения функции f уже характеризуют соответствующие потери в интенсивности потока доходов при конкретном выборе длительности Т периода повторного заказа и параметров γ_i (из-за указанного выше «перехода» к противоположному знаку целевой функции).

Для нахождения оптимальных параметров стратегии управления запасами, характеризующих точку минимума функции f, выпишем соответствующие условия первого порядка (уравнения ∂ f/ ∂ T = 0 и ∂ f/ ∂ γ_i = 0, где i =1,2,…,N):

SD_i ×(1 – γ_i)² ∙[ C_hi + d(C_Пi+Р_Пi) ] + SD_i × γ_i ²∙ С_Вi – 2С₀/T² = 0,

С_Вi∙γ_i – [ С_hi + d(C_Пi + Р_Пi) ] (1 – γ_i) = 0, i=1,2,…,N.

Из второй группы равенств (∂f/∂γ_i = 0, i =1,2,…,N) легко находим:

γ_i = [ С_hi + d(C_Пi + Р_Пi) ] / [ С_hi + d(C_Пi + Р_Пi)+ С_Вi ],

1 – γ_i = С_Вi / [ С_hi + d(C_Пi + Р_Пi)+ С_Вi ].

Как видим, в интересующем нас невырожденном случае анализа имеем γ_iє (0;1) для всех i.

Соответственно из первого равенства для условий первого порядка (∂ f/ ∂ T = 0)

получаем

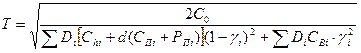
Таким образом, условия первого порядка дают единственное решение для оптимальной стратегии. При этом нетрудно убедиться, что это и есть интересующая нас точка, максимизирующая показатель интенсивности потока доходов при планировании дефицита.

Окончательно, подставляя в найденное выражение для T соответствующие формулы для γ_i и 1 – γ_i определяем оптимальное значение T^* периода повторного заказа при общих поставках для многономенклатурной стратегии планирования дефицита с учетом временной стоимости денег

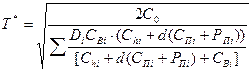
При этом для оптимальной стратегии планирования дефицита в интересующем нас невырожденном случае анализа также имеет место следующее.

q Оптимальное значение размера i- заказа (q_i^*) в партии общей поставки составляет

q_i^* = D_i×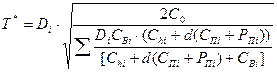

q Оптимальное значение для уровня максимально допустимого дефицита для i- товара (S_i^*) составляет

S_i^* = g_i^*× q_i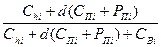^* = × D_i×

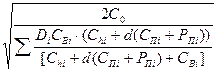
q Оптимальные значения γ_i^* доли времени наличия дефицита для i- товара определяются приведенными выше выражениями для γ_i.

q Оптимальные значения (1-γ_i^*) доли времени наличия запасов для i- товара определяются приведенными выше выражениями для (1-γ_i).

q Оптимальный баланс для длительностей промежутков времени наличия дефицита и наличия запасов для i– товаров определяется пропорцией

.

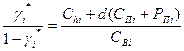Дата добавления: 2015-05-08