Суммарные годовые потери

Указанная величина для анализируемой модели планирования дефицита при управлении запасами без учета временной стоимости денег традиционно в теории управления запасами представляется выражением:

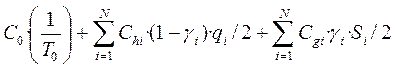
(при любом заданном значении длительности Т₀ интервала времени между общими поставками и при заданных значениях параметров γ_i, характеризующих балансы для промежутков t_1i и t_2i по каждому i -товару в пределах заданного интервала общего повторного заказа). Подчеркнем, что здесь q_i/2 – среднее количество хранимого i -товара на промежутке t_1i. Соответственно величина (1 - γ_i)∙ q_i/2 - среднее количество хранимого товара для всего интервала повторного заказа Т₀. Поэтому, с учетом заданных годовых тарифов C_hi, второе слагаемое в приведенном выше выражении представляет именно суммарные годовые потери из-за хранения товаров. Аналогично, последнее слагаемое представляет годовые потери из-за соответствующего планируемого дефицита.

ЗАДАЧА МИНИМИЗАЦИИ ГОДОВЫХ ПОТЕРЬ

Подставим в указанное выражение вместо q_i и S_i соответствующие формулы, выражающие их через Т₀. Тогда интересующая нас задача минимизации суммарных годовых потерь может быть записана в виде

С₀ ∙ 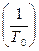+ 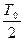∙∑(1-γ_i)² C_hi∙D_i + 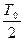∙∑ γ_i ² C_gi∙D_i → min,

причем минимум ищется в области Т₀ > 0, γ_i є [0; 1], i= 1,2,…, N.

ЗАМЕЧАНИЯ 1.

¨ В граничной ситуации, когда γ_i = 0 (дефицит для i- товаров заведомо не планируется), получаем задачу минимизации, решение которой приведено ранее в главе 7.

¨ В другой граничной ситуации, когда γ_i = 1 (заведомо не планируются поставки i- товаров, несмотря на соответствующие штрафные санкции), причем C_gi >0 (невырожденный случай анализа), снова получаем задачу минимизации того же типа, как и в главе 7, но с учетом следующей особенности. В этой ситуации “роль” издержек хранения “исполняют” соответствующие издержки дефицита C_gi, а С₀ - накладные расходы, связанные с погашением издержек дефицита. Соответственно, для нахождения минимума в такой ситуации можно использовать формулы главы 7 с учетом указанной замены.

ЗАМЕЧАНИЯ 2.

Для вырожденного случая анализа, когда C_gi = 0 (издержками дефицита можно пренебречь), отметим следующее.

¨ Соответствующие значения для параметров γ_i, как легко видеть, применительно к такому случаю равны 1. Другими словами, для минимизации потерь i- товары не поставляются.

¨ Разумеется, такое вырожденной решение обусловливается тем, что атрибуты модели не учитывают рентабельности i- товаров.

¨ Соответственно, для менеджеров и лиц, принимающих решения, в такой ситуации потребуются другие подходы к оптимизации стратегии управления запасами, позволяющие учитывать показатели прибыли для i- товаров. В частности, это будет продемонстрировано ниже в рамках соответствующего подхода к оптимизации с учетом временной стоимости денег.

Далее рассматриваем невырожденный случай анализа, когда C_gi >0 и C_hi >0. Интересующая нас задача оптимизации стратегии планирования дефицита (не покрываемого при поставках) в указанном невырожденном случае анализа вполне аналогична задаче оптимизации, рассмотренной в предыдущей главе для стратегии планирования дефицита, покрываемого при очередной поставке. Действительно, формальное представление этих задач отличается (при переходе к задаче планирования непокрываемого при поставках дефицита) лишь заменой показателей тарифов издержек C_Bi от удовлетворяемого дефицита на показатели таких тарифов издержек C_gi от непокрываемого поставками дефицита. Следовательно, для каждого i- товара для параметров γ_i остаются справедливыми равенства γ_i = C_hi/(C_hi+ C_gi), если временная стоимость денег не учитывается. В частности, это позволяет записать интересующую нас задачу минимизации суммарных годовых потерь в более компактном виде. А именно, пусть

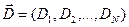- вектор годового потребления i- товаров;

- вектор с компонентами , ;

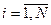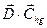- скалярное произведение указанных векторов.

Тогда задача нахождения оптимальной стратегии представляет собой следующую задачу минимизации

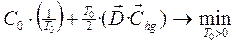
Легко видеть, что задача определения оптимального периода поставки (общей по всем анализируемым товарам) для рассматриваемой в этой главе модели совпадает с аналогичной задачей планирования дефицита, но для модели, рассмотренной в главе 9. Действительно, после формальной замены издержек от не удовлетворяемого поставками дефицита C_gi на издержки C_Bi от покрываемого при очередной поставке дефицита, получаем соответственно эквивалентные выражения.

СЛЕДСТВИЕ. В невырожденном случае анализа (C_gi >0 и C_hi >0) применительно к рассматриваемой модели планирования дефицита (без его покрытия при поставках и без учета временной стоимости денег) основные параметры оптимальной стратегии управления (интервал Т₀* повторного заказа; экономичные размеры заказов q_i* по i -товарам; максимальные размеры S_{i max}* дефицита по i -товарам) можно находить по формулам, приведенным ранее для модели планирования дефицита с его покрытием при очередной поставке партии товаров. При использовании соответствующих формул необходимо:

q выполнить замены, оговоренные выше при анализе задачи оптимизации;

q для нахождения q_i* использовать формулы рассмотренной выше модели планирования дефицита, но относящиеся именно к величине (q_i*-S_i*), т.е. формулы

.

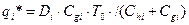Дата добавления: 2015-05-08