Термодинамический процесс и его энергетические характеристики 2 страница

37. Температурное поле и тепловой поток. Законы переноса теплоты.
Температурное поле – совокупность значений температур в пространстве t = f(x,y,z,τ), где:t–температура тела; x,y,z - координаты точки; τ - время.
Тепловой поток – количество теплоты переданная в единицу времени через произвольную поверхность.
Всего существует три простых (элементарных) механизма передачи тепла:

Теплопроводность
Конвекция
Тепловое излучение

Теплопроводность – процесс передачи теплоты в неподвижной среде.
В установившемся режиме плотность потока энергии, передающейся посредством теплопроводности, пропорциональна градиенту температуры:

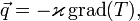
где 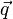— вектор плотности теплового потока — количество энергии, проходящей в единицу времени через единицу площади, перпендикулярной каждой оси, 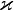— коэффициент теплопроводности (удельная теплопроводность), 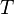— температура. Минус в правой части показывает, что тепловой поток направлен противоположно вектору grad T (то есть в сторону скорейшего убывания температуры). Это выражение известно как закон теплопроводности Фурье.
Конвекция – перенос теплоты конечными объемами текучей среды при её течении под действием определенных сил.

Свободная конвекция – движение среды возникающая в следствии теплообмена под действием силы Архимеда.
Вынужденная конвекция – движение среды инициируется из вне.
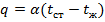- уравнение Ньютона – Рихмана
альфа – коэф. Теплоотдачи.; т_ст – пов-ть стенки примыкающаяся к жидкости; т_ж – жидкость вдали от стенки.
Радиационный теплообмен – заключается в испускании энергии излучением одним телом (т₂) т₂ > т₁, переносом этой энергии в пространство и поглащением этой энергии другим телом с меньшей температурой.

38. Дифференциальное уравнение теплопроводности. Условия однозначности.
Уравнение теплопроводности — важное уравнение в частных производных, которое описывает распространение тепла в заданной области пространства во времени.
Для функции u (x, y, z, t) трёх пространственных переменных (x, y, z) и времени t, уравнение теплопроводности имеет вид

,

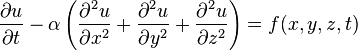где 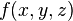— функция тепловых источников.

Для произвольной системы координат:

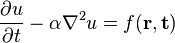
где α — положительная константа, а Δ или ∇2 — оператор Лапласа.
Условия однозначности включают:
- Геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс;
- Физические условия, характеризующие физические свойства тела;
- Временные или начальные условия, характеризующие распределение температур в теле, исследуемой в начальный момент времени;
- Граничные условия, характеризующие взаимодействие тела, рассматриваемого с окружающей средой.

39. Дифференциальное уравнение теплоотдачи, сохранения массы, импульса и энергии.

Дифферциальное уравнение теплоотдачи выводится на основе анализа явления теплообмена в месте соприкосновения теплоносителя со стенкой.

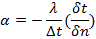
Для трехмерной задачи следует записать это выражение по направлениям осей y и z, после сложения этих выражений получаем дифференциальное уравнение сохранения массы в дифференциальной форме

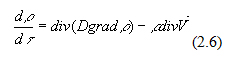
Запишем закон сохранения импульса. Пусть в некоторый момент времени t импульс ракеты равнялся mv. За бесконечно малый промежуток времени dt скорость ракеты увеличилась от v до v + dv, а масса уменьшилась от m до m – dm, и ракета увеличила свой импульс на 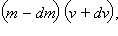выбросив назад dm топлива, импульс которого равен dm (v – u) (здесь и далее уравнение записывается в проекции на ось движения, u > 0). Получаем

Диффиренциальное уравнение энергии

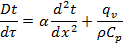
40. Закон Ньютона-Рихмана. Коэффициент теплоотдачи и методы его определения.
Закон Нью́тона — Ри́хмана — эмпирическая закономерность, выражающая тепловой поток между разными телами через температурный напор.

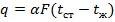
Теплоотдача — это процесс теплообмена между теплоносителем и твёрдым телом.
Теплопередача — это процесс передачи тепла от одной среды к другой через разделяющую их стенку. Закон утверждает, что

Плотность теплового потока (выражается в Вт/м²) на границе тел пропорциональна их разности температур (так называемый температурный напор):

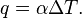
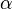— коэффициент теплоотдачи - плотность теплового потока при перепаде температур на 1K, измеряется в Вт/(м²·К). В реальности он не всегда постоянен и может даже зависеть от разности температур, делая закон приблизительным. Если рассматривать тепловой поток как вектор, то он направлен перпендикулярно площадке поверхности, через которую протекает.

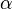— количество теплоты, отдаваемое с 1 м² поверхности за единицу времени при единичном температурном напоре. Он зависит:
от вида теплоносителя и его температуры;
от температуры напора, вида конвекции и режима течения;
от состояния поверхности и направления обтекания;
от геометрии тела.

Поэтому 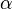— функция процесса теплоотдачи; величина расчётная, а не табличная; определяется экспериментально.

41. Понятие физического подобия. Критерии подобия и методы их получения.
Две и более физические системы называются подо́бными, если при их эволюции сохраняется отношение между некоторыми измеряемыми величинами, характеризующими данные системы. Для подобных систем можно найти так называемые критерии подобия — безразмерные величины, имеющие одинаковое значение для всех систем. Понятие физического подобия обобщает понятие подобия в геометрии.
Критерий подобия — безразмерная величина, составленная из размерных физических параметров, определяющих рассматриваемое физическое явление. Равенство всех однотипных критериев подобия для двух физических явлений и систем — необходимое и достаточное условие физического подобия этих систем.
Число Рейнольдса:

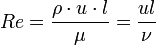. Определяет, в частности, переход от ламинарного режима к турбулентному.

Число Маха:

.
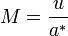Число Фруда:

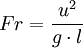
В этих примерах

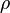— плотность жидкости или газа,

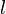— характерный размер,

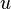— скорость течения,

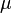— динамический коэффициент вязкости,

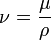— кинематический коэффициент вязкости,

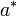— местная скорость распространения звука в движущейся среде.

Каждый из критериев подобия имеет определенный физический смысл как величина, пропорциональная отношению однотипных физических величин. Так, число 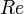характеризует отношение инерционных сил при движении жидкости или газа к силам вязкости, а число — отношение инерционных сил к силам тяжести.

Основными критериями подобия процессов теплопередачи между жидкостью (газом) и обтекаемым телом являются число Прандтля 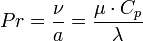, число Нуссельта 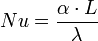, число Грасгофа 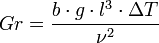, а также число Пекле 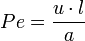и число Стэнтона 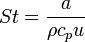. Здесь 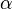— коэффициент теплоотдачи, 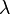— коэффициент теплопроводности, 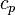— удельная теплоёмкость жидкости или газа при постоянном давлении, — коэффициент температуропроводности, b — коэффициент объёмного расширения, 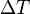— разность температур поверхности тела и жидкости (газа). Два последних числа связаны с предыдущими соотношениями: Ре = Pr×Re, St = Nu/Pe.

42. Уравнения подобия, их структура для естественной и вынужденной конвекции.
Согласно положений теории подобия конвективный теплообмен без изменения агрегатного состояния вещества в стационарных условиях может быть описан критериальным уравнением вида:

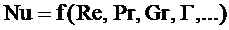, (1.3)

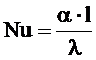- критерий Нуссельта, характеризующий подобие процессов теплопереноса на границе между стенкой и потоком жидкости;

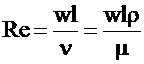- критерий Рейнольдса, который характеризует гидродинамический режим потока при вынужденном движении и является мерой соотношения сил инерции и вязкого трения;

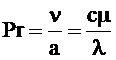- критерий Прандтля, который характеризует физико – химические свойства теплоносителя и является мерой подобия температурных и скоростных полей в потоке;

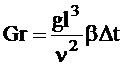- критерий Грасгофа, характеризующий соотношение сил вязкого трения и подъемной силы, описывает режим свободного движения теплоносителя;

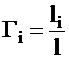- безразмерный геометрический симплекс, характеризующий геометрическое подобие системы.
Для расчета числа критерия Нуссельта при вынужденном движении потока в прямых трубах или каналах можно рекомендовать следующие уравнения:

а) для ламинарного режима движения теплоносителя, :

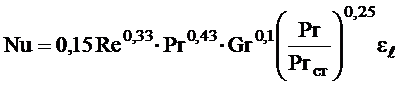, (1.5)

где - критерий Прандтля для теплоносителя при температуре стенки;

б) для переходного режима движения теплоносителя, :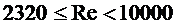

.
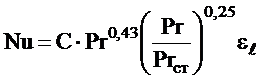в) для турбулентного режима движения теплоносителя, :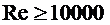

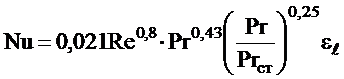
При свободном движении теплоносителя (естественная конвекция):

.

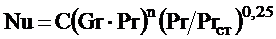43. Теплопроводность плоской стенки при стационарном режиме. Виды граничных условий.
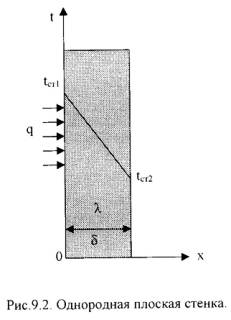Температуры поверхностей стенки –tст1 и tст2. Плотность теплового потока: q = -λ∙ ∂t/∂n = - λ∙ ∂t/∂x = - λ∙ (tcт2 - tcт1)/(xcт2 - xcт1)∙ или q = λ∙ (tcт2 - tcт1)/(xcт2 - xcт1)∙ Dt/Dx. Тогда q = λ/δ∙(tст1 – tст2) = λ/δ∙Δt, Если R =δ/λ -термическое сопротивление теплопроводности стенки [(м2∙К)/Вт], то плотность теплового потока: q = (tст1 – tст2)/R. Общее количество теплоты, которое передается через поверхность F за время τ определяется: Q = q∙F∙τ = (tст1 – tст2)/R·F∙τ. Температура тела в точке с координатой х находится по формуле: tx = tст1 – (tст1 – tст2)∙x/ δ.
граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:

1) первого рода, задается распределение температуры на поверхности тела в функции времени;

2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;

3) третьего рода, задаются температура окружающей среды t_ж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:

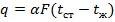
где t_c — температура поверхности тела; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м²·К), F – площадь боковой поверхности.

44. Теплопроводность многослойной плоской стенки при граничных условиях первого рода. Термическое сопротивление.

Наклон температурной линии в отдельных слоях различен. Это объясняется тем, что для всех слоев:
Поэтому слои с меньшим коэффициентом теплопроводности имеют больший температурный градиент и, следовательно, больший наклон температурной линии.
Термическое сопротивление — тепловое сопротивление, способность тела (его поверхности или какого-либо слоя) препятствовать распространению теплового движения молекул.
Виды термического сопротивления

Различают полное термическое сопротивление — величину, обратную коэффициенту теплопередачи, поверхностное термическое сопротивление — величину, обратную коэффициенту теплоотдачи, и термическое сопротивление слоя, равное отношению толщины слоя к его коэффициенту теплопроводности.
Общая формула:

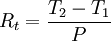
где: 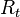— тепловое сопротивление на участке тепловой цепи, K / Вт, 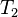— температура начала участка, K, 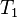— температура конца участка, K, 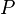— тепловой поток, протекающий через участок цепи, Вт
Тепловое сопротивление участка цепи постоянного сечения:
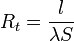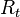где: — тепловое сопротивление участка цепи, К/Вт, 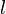— длина участка тепловой цепи, м, 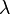— коэффициент теплопроводности материала, Вт/(м К), 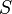— площадь поперечного сечения участка, м², Rк= R1+R2+R3…..Rn

45. Теплопроводность цилиндрической стенки при граничных условиях первого рода.
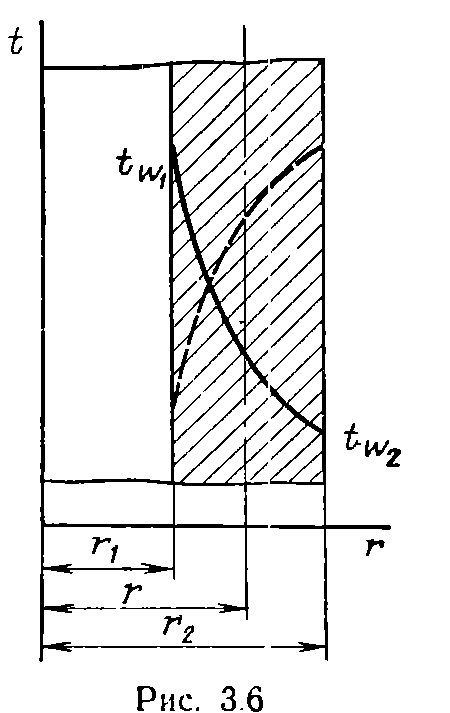Температуры поверхностей стенки –tст1 и tст2. Уравнение теплопроводности по закону Фурье в цилиндрических координатах: Q = - λ∙2∙π∙r ·l· ∂t / ∂r или Q = 2·π·λ·l·Δt/ln(d2/d1), где: Δt = tст1 – tст2 – температурный напор; λ – κоэффициент теплопроводности стенки. Для цилиндрических поверхностей вводят понятия тепловой поток единицы длины цилиндрической поверхности (линейная плотность теплового потока), для которой расчетные формулы будут: ql = Q/l =2·π·λ·Δt /ln(d2/d1), [Вт/м]. Температура тела внутри стенки с координатой dх:tx = tст1 – (tст1 – tст2) ·ln(dx/d1) / ln(d2/d1).
Количество теплоты, переданной от горячей среды к внутренней стенке трубы по закону Ньютона-Рихмана имеет вид: Q = p·d1·a1·l·(t'ж – t1), где a1 – коэффициент теплоотдачи от горячей среды с температурой t'ж к поверхности стенки• с температурой t1; Тепловой поток, переданный через стенку трубы определяется по уравнению: Q = 2·p·l·l·(t1 – t2) / ln (d2/d1). Тепловой поток от второй поверхности стенки трубы к холодной среде определяется по формуле: Q = p·d2·a2·l·(t1 - t''ж), где a2 – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t''ж. Решая эти три уравнения получаем: Q = p l·(t'ж – t''ж) • К, где Кl = 1/[1/(a1d1)+ 1/(2lln(d2/d1) + 1/(a2d2)] –- линейный коэффициент теплопередачи, или Rl = 1/ Кl = [1/(a1d1)+ 1/(2lln(d2/d1) + 1/(a2d2)] –полное линейное термическое сопротивление теплопередачи через однослойную цилиндрическую стенку. 1/(a1d1), 1/(a2d2) – термические сопротивления теплоотдачи поверхностей стенки; 1/(2lln(d2/d1) - термическое сопротивление стенки. Для многослойной (n слоев) цилиндрической стенки полное линейное термическое сопротивление будет определяться по следующей формуле: Rl = 1/ Кl = [1/(a1d1)+ 1/(2l1ln(d2/d1) + 1/(2l3ln(d3/d2) + … + 1/(2lnln(dn+1/dn) + 1/(a2dn)]

46. Теплопроводность плоской стенки при граничных условиях третьего рода. Коэффициент теплоотдачи.
Граничные условия третьего рода (теплопередача).
Передача теплоты из одной среды (жидкости или газа) к другой через разделяющую их однородную или многослойную твердую стенку любой формы называется теплопередачей. Теплопередача включает в себя теплоотдачу от более горячей жидкости к стенке, теплопроводность в стенке, теплоотдачу от стенки к более холодной среде.
Рассмотрим теплопередачу через однородную и многослойную плоские стенки.
Пусть плоская однородная стенка имеет толщину δ (рис. 2.3). Заданы коэффициент теплопроводности стенки λ, температуры окружающей среды t_f1 и t_f2, а также коэффициенты теплоотдач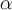и ₁ и 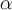₂; будем считать, что величины t_f1, t_f2 , 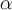₁ и 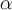₂ постоянны и не меняются вдоль поверхности. Это позволяет рассматривать изменение температуры жидкостей и стенки только в направлении, перпендикулярном плоскости стенки.

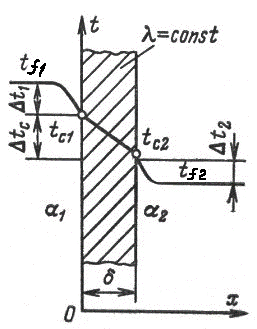
Теплопередача через плоскую стенку.

46. Коэффициент теплоотдачи

Теплоотдача – это теплообмен между теплоносителем и твердым телом.

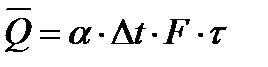
Закон Ньютона-Рихмана о теплоносителях

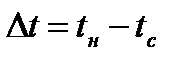
Количество теплоты, передаваемое на границы площадью F за время t, пропорционально температурному напору.
a - коэффициент теплоотдачи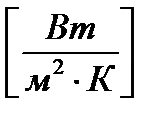
a - количество теплоты, отдаваемое с 1 м² поверхности за единицу времени при единичном температурном напоре.

a зависит:

от вида теплоносителя и его температуры;

от температуры напора, вида конвекции и режима течения;

от состояния поверхности и направления обтекания;

от геометрии тела

a - функция процесса теплоотдачи; величина расчетная, а не табличная; определяется экспериментально.

47. Обратный термодинамический цикл. Термотрансформаторы.

Обратный круговой процесс может осу­ществляться тремя циклами: холодильным, теплового насоса и теплофикационным (одновременное получение тепла и хо­лода).
Холодильный цикл совершается между температурами охла­ждаемого тела Т₀ и окружающей среды Т. Цикл теплового насоса между температурами окружающей среды и нагретого тела. Теплофикацион­ный цикл между температурами холодного Т₀ и горячего тела Тг.
Обратный цикл может быть разомкнут без нарушения составляющих его термо­динамических процессов. После совершения только одной части цикла тер­модинамические процессы могут быть пре­кращены и затем возобновлены в другое время или в другом месте. Примерами разомкнутого цикла может служить производ­ство твердой углекислоты (сухой лед) ж жидкого воздуха. Для получения сухого льда газообразная углекислота сжимается компрессором до определенного давления, затем благодаря отводу тепла окружающей средой сжижается. Жидкая углекислота дросселируется до более низкого давления, при котором образуется ее твердая фаза. Цикл прекращается, твердая углекислота извлекается и сохраняется для получения холодильного эффекта в другом месте. При этом сублимирующая твердая фаза пре­вращается в газообразную и каждая еди­ница массы производит количество холода, соответствующее холодильному эффекту данного замкнутого термодинамического цикла.

48. Эксэргия и ее применение

Эксергия - часть энергии, равная максимальной полезной работе работа, которую может совершить термодинамическая система при переходе из данного состояния в состояние равновесия с окружающей средой.
Эксергией иногда называется работоспособность системы.
Использование понятия эксергии даёт возможность количественно определить влияние неравновесия термодинамических процессов на эффективность преобразования энергии, то есть позволяет вычислять особенности второго начала термодинамики: выделить ту часть энергии, которая не может быть использована из-за газодинамических явлений, трения, теплообмена. Такой подход даёт возможность анализировать степень термодинамической доскональности того или другого элемента установки и не требует предварительной оценки работоспособности всей установки в целом.

49. Классификация и принципы расчёта теплообменников.

Устройство, предназначенное для передачи теплоты от более нагретого теплоносителя до менее нагретого.

В зависимости от способа организации процесса различают:
- смесительные теплообменники, в которых теплообмен осуществляется в непосредственном контакте с теплоносителем;
- поверхностные теплообменники, где теплоносители разделены твердой стенкой;
- регенеративные теплообменники, в которых теплоносители поочередно контактируют с аккумулятором теплоты представляющим, как правило, насыпку из химически нейтрального материала, например керамики.
Наиболее распространенные – поверхностные теплообменники. Их эффективность главным образом определяет качество и экономичность современных теплоэнергетических систем.

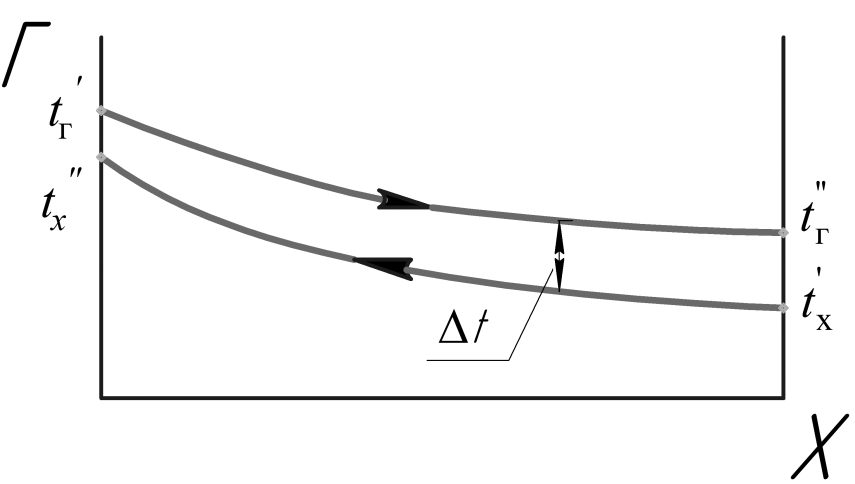
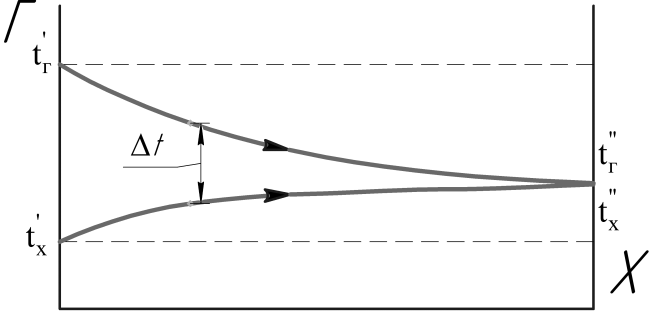
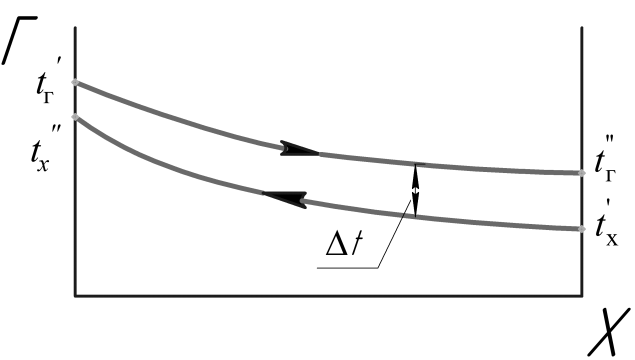
Схема движения прямоток

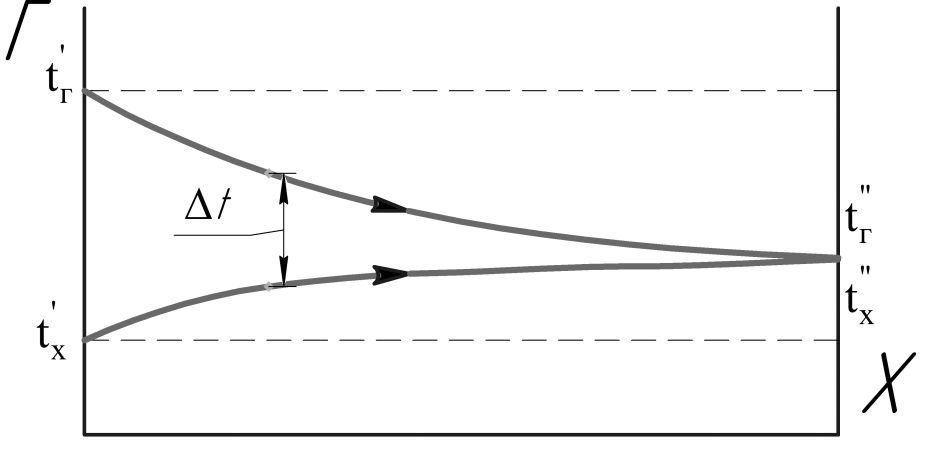
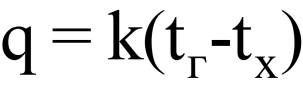
Схема противоточного движения обладает преимуществом, что позволяет получить температуру одного из теплоносителей на входе равный температуре другого теплоносителя на входе. При такой схеме движения температурный напор более однородной температуре в теплообменнику, что позволяет уменьшить его габариты.

Поэтому схема противоток применяется, повсюду, где это конструктивно возможно.

49. Тепловой расчет

Подразделяют на проектировочный и поверочный. Цель проектировочного расчета: при заданных тепловом потоке, начальных температурах теплоносителей и в виде теплообменной поверхности определить площадь теплообмена позволяющую обеспечить требуемый тепловой поток. Цель поверочного расчета: при заданной геометрии теплообменника и начальных температурах теплоносителей их расход определить тепловой поток в этом теплообменнике.
Независимо от вида расчета основные расчетные соотношения сохраняются. Геометрия теплообменника и свойства теплоносителей, включая их расход, позволяют в каждом сечении определить коэффициент теплопередачи.

50. Схема движения теплоносителей и температурный напор при теплообмене.

Температурный напор — разность характерных температур среды и стенки (или границы раздела фаз) или двух сред, между которыми происходит теплообмен.
Местный температурный напор — разность температур среды и местной температуры стенки (границы раздела фаз) либо разность температур двух сред в данном сечении теплообменной системы.
Средний температурный напор — температурный напор, осреднённый по поверхности теплообмена.
Произведение значения температурного напора на коэффициент теплопередачи определяет количество теплоты, передаваемое от одной среды к другой через единицу поверхности нагрева в единицу времени, то есть плотность теплового потока.

Дата добавления: 2015-05-09