Статистический смысл энтропии. Энтропия идеального газа. Флуктуации

Запись с использованием оператора Лиувилля

Запись через скобку Пуассона

Используя скобку Пуассона, имеющее в канонических координатах 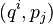вид

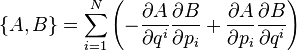
уравнение Лиувилля для гамильтоновых систем приобретает вид

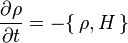
При помощи оператора Лиувилля

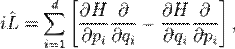
для гамильтоновых систем уравнение приобретает вид

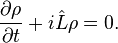
Рассмотрим закрытый сосуд, разделенный перегородкой 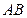, на две одинаковые част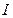и и 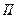. Пусть в части сосуда 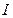находится 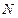молекул идеального газа, а в части 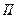– ни одной. В момент времени 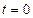мгновенно удалим перегородку. Молекулы из части 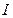начнут переходить в часть 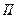. В какой-то момент времени количества молекул в первой и второй частях примерно выровняются. Так же выровняются потоки туда и обратно. Мы будем наблюдать динамическое равновесие, а не статистическое.

Статистическое равновесие предполагает, что 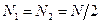, а в нашем случае это правила почти никогда не соблюдается. Для такой системы нужно оперировать не мгновенными значениям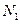и и 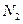, а их средними значениями, взятыми за достаточно длительный промежуток времени: 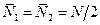. Самопроизвольные отклонения чисел 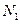и 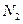, а так же любых других физических величин от их средних значений, обусловленные тепловым движением, называются флуктуациями.

Рассмотрим сосуд всего с одной молекулой идеального газа. Она равновероятно может попасть в часть сосуда 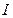или 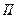. Вероятность такого попадания 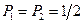. Введем в сосуд вторую молекулу. Молекулы идеального газа не взаимодействуют между собой и их попадания в ту или иную часть сосуда – события независимые. Вероятность того, что они обе окажутся в части сосуда 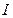(по теореме умножения вероятностей): 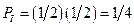. Если в сосуде 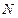молекул, то вероятность их общего попадания в часть 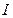будет 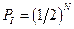. Если полный объем сосуда 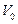, то вероятность попадания отдельной молекулы идеального газа в некоторый объем 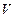, выделенный из общего объема, равна 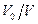. Вероятность того, что в 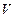окажутся 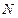молекул, равна

.

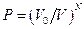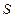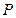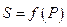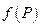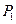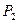Предположим, что между энтропией и вероятностью есть связь, выражающаяся формулой , где – одна и та же для всех тел. Рассмотрим две независимые подсистемы в состояниях с вероятностями и . Энтропии этих состояни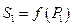й – и 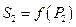. Объединим подсистемы в систему и обозначим вероятность ее состояния через 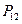, а энтропию через 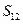. Т.к. подсистемы независимы, то 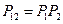, значит 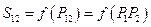. Учтем, что энтропия сложной системы должна быть равна сумме энтропий составляющих ее независимых подсистем

. Из этого следует, что 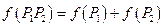. Предположим, что переменные 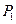и 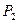изменяются так, что 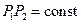, тогда 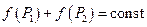. Продифференцируем оба выражения и получим: 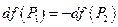, при условии 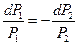. После почленного деления –

.

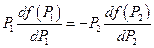Т.к. в левой и правой частях разные 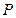, то можно сделать вывод, что функция

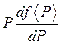
не изменяется при изменении аргумента. Это значит она является некой универсальной постоянной (обозначим ее через 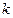), одной и той же для всех тел.

.

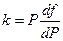
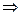
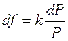
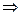
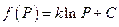Подставим последнее соотношение в уравнение 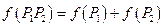и получим

,

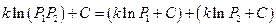откуда .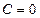

Значит 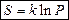– уравнение Больцмана.

Пусть 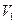и 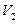– объемы моля газа в начальном и конечном состоянии при одной и той же температуре. Отношения вероятностей найдем по формуле 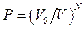, поочередно предположив: 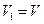, 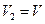. Далее найдем разность энтропий

.

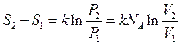Из определения энтропии известно, что если теплоемкость 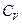не зависит от температуры, то

,

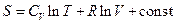тогда .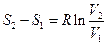

Сравнивая два уравнения для 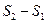, получим – постоянная Больцмана.

Дата добавления: 2015-05-09