Цикл Карно. Французский инженер Сади Карно в 1824 г

Французский инженер Сади Карно в 1824 г. предложил обратимый цикл тепловой машины, рабочим телом в котором является идеальный газ. Цикл Карно осуществляется между двумя внешними источниками постоянных температур Т₁ и Т₂ и состоит из двух адиабат и двух изотерм (рис. 12).

Подвод теплоты от горячего источника производится на изотерме А-В при температуре Т₁, при этом рабочее тело - идеальный газ расширяется и совершается полезная работа. В процессе дальнейшего расширения по адиабате В-С до температуры Т₂ также совершается полезная работа. Для осуществления последующих процессов - сжатия C-D по изотерме Т₂ с отводом теплоты к холодному источнику и адиабатного сжатия D-A до начальной температуры Т₁ работа затрачивается.

В силу того, что в цикле используется идеальный газ, для которого ранее было установлен принцип существования энтропии, этот цикл можно также изобразить и в координатах T-S (рис. 12б).

Рис. 12. Цикл Карно для теплового двигателя

Графически цикл Карно в T-S координатах представляет собой прямоугольник, так как изотермы и адиабаты в этих координатах изображаются прямыми линиями.

Согласно принципу существования энтропии для идеальных газов () (75) интегральные количество подведенной и отведенной теплоты в цикле Карно может быть определено из следующих соотношений:

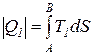= = ; (146)

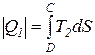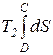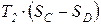= = . (147)

Для замыкания цикла необходимо, чтобы итоговое изменение энтропии (как функции состояния) в цикле было равно нулю

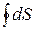= 0, (148)

следовательно

. (149)

Количества подведенной и отведенной теплоты равны соответственно:

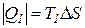, (150)

, (151)

а работа цикла составляет

. (152)

Согласно определению КПД термодинамического цикла тепловых двигателей (141) выражение коэффициента полезного действия цикла Карно можно представить в следующем виде:

. (153)

Соответственно, холодильный коэффициент обратного цикла Карно для холодильной машины определяется соотношением

. (154)

Полученные соотношения (153) и (154) свидетельствуют о том, что КПД и холодильный коэффициент обратимого цикла Карно зависят только от соотношения абсолютных температур горячего Т₁ и холодного Т₂ источ-ников теплоты.

Анализ соотношения (153) показывает, что КПД цикла Карно возрастает с увеличением температуры горячего и при понижении температуры холодного источников.

Цикл Карно для теплотехники имеет большое значение. Он позволяет определить наивысшее значение термодинамического КПД теплового двигателя, работающего в диапазоне значений температуры рабочего тела в процессах подвода (Т₁) и отвода (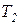) теплоты. При этом цикл Карно является эталоном: с КПД цикла Карно сравнивают КПД циклов реальных тепловых двигателей и определяют их термодинамическое совершенство.

Дата добавления: 2015-05-09