Энтропия. Количественной характеристикой теплового состояния тела, описывающей его стремление переходить в другие состояния

Количественной характеристикой теплового состояния тела, описывающей его стремление переходить в другие состояния, является число микроскопических способов, которым это состояние может быть осуществлено. Это число называют статистическим весом состояния; обозначим его буквой Г. Тело, предоставленное самому себе, стремится перейти в состояние с большим статистическим весом. Принято, однако, пользоваться не самим числом Г, а его логарифмом, который еще умножают на постоянную Больцмана k. Определенную таким образом величину

S = k lnГ

называют энтропией тела.

Число способов Г, которыми может осуществиться состояние системы, состоящей, например, из двух тел, равно, очевидно, произведению чисел способов Г₁ и Г₂, которыми могут быть осуществлены состояния каждого из этих тел в отдельности: Г=Г₁ × Г₂. Поэтому

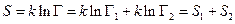
Мы видим, что энтропия сложной системы равна сумме энтропии ее частей (именно для достижения этого свойства и служит логарифм в определении энтропии). Закон, определяющий направление тепловых процессов, можно сформулировать как закон возрастания энтропии:

при всех происходящих в замкнутой системе тепловых процессах энтропия системы возрастает; максимальное возможное значение энтропии замкнутой системы достигается в тепловом равновесии. Это утверждение является более точной количественной формулировкой второго закона термодинамики. Этот закон был открыт Клаузиусом, а его молекулярно-кинетическое истолкование было дано Больцманом.

Обратно, можно сказать, что всякий процесс, при котором энтропия замкнутой системы тел возрастает, является необратимым; чем больше возрастание энтропии, тем больше степень необратимости. Идеальному случаю полностью обратимого процесса соответствует случай, когда энтропия замкнутой системы оставалась бы неизменной.

Точное определение того, что именно подразумевается под «числом микроскопических способов осуществления» теплового состояния тела, дается в статистической физике. Только после этого появляется возможность фактического вычисления энтропии различных тел и установления ее связи с другими тепловыми величинами.

Более глубокий теоретический анализ позволяет установить соотношение, являющееся основой для термодинамических применений понятия энтропии. Это соотношение связывает изменение dS энтропии тела при бесконечно малом обратимом изменении его состояния с количеством получаемого им в этом процессе тепла dQ. Речь идет при этом о незамкнутом теле, так что обратимость процесса не требует постоянства его энтропии! Оно имеет вид

где Т – температура тела.

Самый факт существования связи между dS и dQ вполне естественен. Сообщение телу тепла приводит к усилению теплового движения его атомов, т. е. к увеличению хаотичности их распределения по различным состояниям микроскопического движения, а тем самым к увеличению статистического веса. Естественно также, что влияние заданного количества тепла на изменение теплового состояния тела характеризуется относительной величиной этого количества по сравнению с полной внутренней энергией тела и потому убывает с увеличением его температуры. Соотношение dQ=TdS приводит, в частности, к указанному уже выражению для к. п. д. цикла Карно. В этом процессе участвуют три тела: нагреватель, охладитель и рабочее тело. Последнее в результате цикла возвращается в исходное состояние, так что и его энтропия возвращается к исходному значению. Условие обратимости процесса – требование неизменности полной энтропии системы – сводится поэтому к постоянству суммы энтропии S₁ охладителя и S₂ нагревателя. Пусть при цикле охладитель получает некоторое малое количество тепла ΔQ₁, a нагреватель отдает тепло ΔQ₂. Тогда

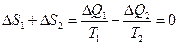
откуда

.

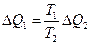Работа в одном цикле: 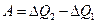, а потому

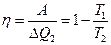
Дата добавления: 2015-05-09