Политропические процессы

Все рассмотренные ранее процессы являются частными случаями политропического процесса.

Таблица.

n	Процесс
	Изобарический
	Изотермический
g	Адиабатический
± ¥	Изохорический

Политропическим называется такой процесс, при котором давление и объем идеального газа связаны соотношением

pVⁿ = const, (104.1)

где n может принимать значения от – ¥ до + ¥. В таблице указаны значения n, при которых политропический процесс оказывается тождественным с одним из уже известных процессов. Первые три строки таблицы очевидны. Чтобы убедиться в справедливости четвертой строки, можно представить уравнение политропы (104.1) в следующем виде:

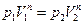(104.2)

где индексы 1 и 2 относятся к двум произвольно взятым состояниям. Отсюда:

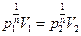
При n ® ± ¥ получается условие V₁ = V₂, которое характеризует изохорический процесс.

Работа, совершаемая идеальным газом при различных процессах

Работа, которая совершается при переходе из состояния 1 в состояние 2 каким–либо телом над внешними телами, равна, как известно (см. (96.3)):

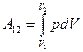(105.1)

Чтобы произвести интегрирование, нужно выразить р через V. Для этого воспользуемся связью между р и V при различных процессах. Уравнение политропы идеального газа (104.1) можно написать следующим образом:

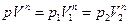
где p₁, V₁ и p₂, V₂ – значения давления и объема газа соответственно в первом (начальном) и втором (конечном) состояниях, р и V – давление и объем в любом промежуточном состоянии. В соответствии с этим соотношением давление газа выражается через его объем и значения параметров в начальном состоянии 1:

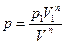(105.2)

Тогда (105.1) приобретает вид:

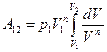(105.3)

Пусть n ≠ 1; тогда интеграл в (105.3) равен

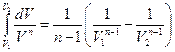
Тогда работа (105.3) равна:

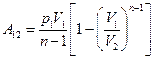(105.4)

Полученное выражение можно преобразовать, воспользовавшись тем, что, какой бы процесс ни происходил с идеальным газом, его параметры связаны уравнением состояния (98.14). В частности, это справедливо и для начального состояния:

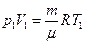
Отсюда:

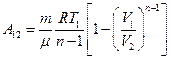(105.6)

Выражения (105.4) и (105.6) дают работу, совершаемую идеальным газом при любом политропическом процессе, кроме изотермического (n = 1).

Работа идеального газа при изотермическом процессе вычисляется после представления давления в формуле (105.1) через другие величины в соответствии с уравнением состояния. В результате Т можно вынести за знак интеграла, поскольку она постоянна:

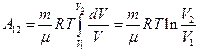
Итак, работа, совершаемая идеальным газом при изотермическом процессе, равна

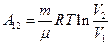(105.9)

При изобарическом процессе работа, совершаемая любым телом, в том числе и идеальным газом, равна, как следует из (105.1),

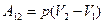(105.10)

Тот же результат получается, если положить в (105.4) n равным нулю.

В заключение следует отметить, что при изохорическом процессе работа равна нулю, что справедливо для любых тел.

Дата добавления: 2015-05-09