Равнораспределение энергии по степеням свободы

Полученное выше выражение для средней энергии молекулы

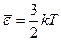(101.1)

учитывает только энергию поступательного движения молекулы, то есть движение центра масс. Однако возможны и другие, внутренние, формы движений молекулы: её вращение и колебания атомов, образующих молекулу. Эти виды движения связаны с некоторым запасом энергии, определяемым в статистической физике положением о равнораспределении энергии по степеням свободы молекулы.

Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы.

Так, положение в пространстве материальной точки полностью определяется заданием значений трех ее координат (декартовых х, у, z или сферических r, q, j и т. д.). Соответственно материальная точка имеет три степени свободы.

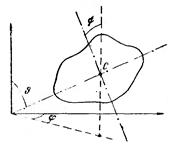
Положение абсолютно твердого тела определяется тремя координатами центра масс (x,y,z), двумя углами q и j, определяющими ось, связанную с телом и проходящую через его центр масс (рис.), и, наконец, углом y, определяющим направление второй связанной с телом оси, перпендикулярной к первой. То есть абсолютно твердое тело имеет шесть степеней свободы. Изменение координат центра масс при неизменных углах q, j и y обусловлено поступательным движением твердого тела. Поэтому соответствующие степени свободы называются поступательными. Изменение любого из углов q, j и y при неизменном положении центра масс определяется вращением тела. Соответствующие степени свободы называются вращательными. Следовательно, из шести степеней свободы абсолютно твердого тела три являются поступательными и три – вращательными.

Система из N материальных точек, между которыми нет жестких связей, имеет 3N степеней свободы (положение каждой из N точек должно быть задано тремя координатами). Любая жесткая связь, устанавливающая неизменное взаимное

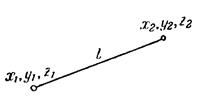
расположение двух точек, уменьшает число степеней свободы на единицу. Например, если система состоит из двух материальных точек, расстояние l между которыми остается постоянным (рис.), то число степеней свободы системы равно пяти. В самом деле, в этом случае между координатами точек имеется соотношение:

(x₂ – x₁)² + (y₂ – y₁)² + (z₂ – z₁)² = l ²

вследствие чего координаты не будут независимыми. Достаточно задать любые пять координат, шестая определится приведенным условием.

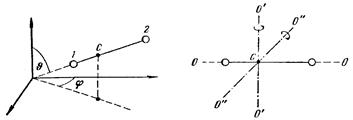
Классифицируются эти степени свободы заданием параметров, определяющих движение молекулы. Например, для системы, состоящей из двух жестко связанных материальных точек, задаются три координаты центра масс системы (рис.) и два угла q, j, которыми определяется направление в пространстве оси системы (т. е. прямой, проходящей через обе точки). Отсюда следует, что три степени свободы будут поступательными и две – вращательными. Вращательные степени свободы соответствуют вращениям вокруг двух взаимно–перпендикулярных осей О'О' и О"О", перпендикулярных к оси системы 00 (рис.). Вращение вокруг оси 00 для материальных точек лишено смысла.

Если две материальные точки связаны не жесткой связью, а упругой (при изменении равновесного расстояния между точками появляется сила, восстанавливающая первоначальное расстояние между точками), то число степеней свободы равно шести. Положение системы в этом случае задается тремя координатами центра масс (рис.), двумя

углами q и j и расстоянием между точками r. Изменения r соответствуют колебаниям в системе, вследствие чего эту степень свободы называют колебательной. Итак, рассмотренная система имеет три поступательные, две вращательные и одну колебательную степень свободы.

Система состоящая из N упруго связанных друг с другом материальных точек, имеет 3N степеней свободы. Существует равновесная конфигурация точек, отвечающая минимуму потенциальной энергии системы. Равновесная конфигурация характеризуется определенными расстояниями между точками. Если точки вывести из положений равновесия, в системе возникнут колебания. Положение системы можно определить, задав положение равновесной конфигурации и величины смещения точек из равновесных положений. Они соответствуют колебательным степеням свободы. Положение равновесной конфигурации, как и положение абсолютно твердого тела, определяется шестью величинами, которым соответствуют три поступательные и три вращательные степени свободы. Предполагается, что равновесные положения точек не лежат на одной прямой. В противном случае вращательных степеней свободы будет только две, а колебательных 3 N – 5. Это случай системы, состоящей нз двух точек. Таким образом, количество колебательных степеней свободы равно 3N – 6.

Из результатов измерений теплоемкости газов следует, что при определении числа степеней свободы молекулы атомы следует рассматривать как материальные точки. Следовательно, одноатомной молекуле нужно приписывать три поступательные степени свободы, двухатомной молекуле, в зависимости от характера связи между атомами, следует приписывать либо три поступательные и две вращательные степени свободы (при жесткой связи), либо, кроме этих пяти, еще одну, колебательную степень свободы (при упругой связи), трехатомной молекуле с жесткой связью – три поступательные и три вращательные степени свободы и т. д.

В любом случае, сколько бы степеней свободы ни имела молекула, три из них – поступательные. Поскольку ни одна из поступательных степеней свободы молекулы не имеет преимущества перед остальными, на каждую из них должна приходиться в среднем одинаковая энергия, равная kT/2.

Больцман предположил, что ни один из видов движения не имеет преимущества перед другими и, следовательно, на любую степень свободы – поступательную, вращательную и колебательную – должна приходиться в среднем одинаковая кинетическая энергия, равная kT/2. Это утверждение и представляет собой содержание положения о равнораспределении энергии по степеням свободы. Справедливость этого положения подтверждается измерениями теплоемкостей газов (см. ниже). Согласно положению о равнораспределении среднее значение энергии одной молекулы e будет (при той же температуре) тем больше, чем сложнее молекула, чем больше у нее степеней свободы. При определении e нужно учесть, что колебательная степень свободы должна обладать вдвое большей энергетической емкостью по сравнению с поступательной или вращательной. Это объясняется тем, что поступательное и вращательное движение молекулы связано с наличием только кинетической энергии, в то время как колебательное движение связано с наличием и кинетической, и потенциальной энергии, причем для гармонического осциллятора средние значения кинетической и потенциальной энергии равны. Поэтому на каждую колебательную степень свободы должны приходиться в среднем две половинки kT – одна в виде кинетической энергии и одна в виде потенциальной. Таким образом, средняя энергия молекулы должна равняться:

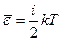(101.3)

где i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекулы:

i = n _пост + n _вращ + 2 n _колеб (101.4)

Для молекул с жесткой связью между атомами i совпадает с числом степеней свободы молекулы.

Дата добавления: 2015-05-09