Уравнение кинетической теории газов для давления

Простейшая молекулярно-кинетическая модель газа выглядит следующим образом. Газ – это совокупность одинаковых, хаотически движущихся, не взаимодействующих друг с другом на расстоянии молекул. Размеры молекул столь малы, что суммарным объемом их можно пренебречь по сравнению с объемом сосуда. Подавляющую часть времени каждая молекула движется свободно, претерпевая иногда упругие соударения с другими молекулами или со стенками сосуда. Такая модель представляет собой не что иное, как идеальный газ. У реальных газов молекулы обладают конечными размерами и взаимодействуют друг с другом с силами, зависящими от расстояния между молекулами. Только при малых плотностях газа собственный объем молекул мал по сравнению с объемом, занимаемым газом, а средние расстояния между молекулами так велики, что силами взаимодействия молекул друг с другом можно пренебречь.

При ударе о стенку сосуда молекула сообщает ей импульс, численно равный изменению импульса молекулы. Каждый элемент поверхности стенки DS непрерывно подвергается бомбардировке большим количеством молекул, в результате чего за время Dt получает суммарный импульс DК, направленный по нормали к DS. Отношение DК/Dt дает, как известно из механики, силу, действующую на DS, а отношение этой силы к DS даст давление р.

Молекулы движутся совершенно беспорядочно, хаотически; все направления движения равновероятны. Основанием для такого утверждения служит то обстоятельство, что давление газа на стенки сосуда всюду одинаково. Если бы движение молекул в каком-то направлении преобладало, давление газа на участок стенки, лежащий в этом направлении, было бы, естественно, больше.

Скорости молекул могут быть самыми различными по величине. Более того, скорость молекулы должна меняться, вообще говоря, при каждом соударении, причем с равной вероятностью она может, как возрасти, так и уменьшиться. Это следует из того, что суммарная кинетическая энергия двух молекул до и после их соударения должна быть одинакова. Следовательно, возрастание скорости одной молекулы должно сопровождаться одновременным уменьшением скорости другой.

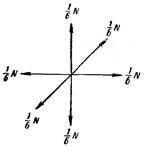
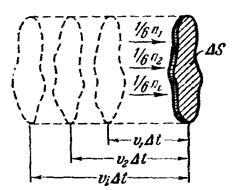
Для облегчения решения поставленной задачи вводят некоторые упрощения, касающиеся характера движения молекул. Во-первых, предполагается, что молекулы движутся только вдоль трех взаимно перпендикулярных направлений. Если газ содержит N молекул, то в любой момент времени вдоль каждого из направлений будет двигаться N/3 молекул, причем половина из них (т. е. N/6) движется вдоль данного направления в одну сторону, половина в противоположную (рисунок). Отсюда следует, что в нужном направлении (например, по нормали к данному элементу стенки DS) движется 1/6 часть молекул. Второе упрощение: все молекулы движутся со скоростью V. Первое упрощение не влияет на конечный результат вычисления давления; уточнения, к которым приводит отказ от второго упрощения, будут выяснены ниже.

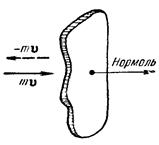
Вычисление импульса, сообщаемого стенке сосуда ударяющейся о нее молекулой достаточно просто. До удара о стенку импульс молекулы направлен по внешней нормали к DS (рис.) и равен mV. В результате удара импульс меняет знак. Таким образом, приращение импульса молекулы оказывается равным

(- m v)-(m v)= -2 m v. (99.1)

По третьему закону Ньютона стенка получает при ударе импульс 2m v, имеющий направление нормали. За время Dt до элемента стенки DS долетят все движущиеся по направлению к нему молекулы, заключенные в объеме цилиндра с основанием DS и высотой vDt (рис.). Число этих молекул равно

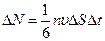(99.2)

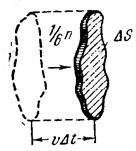
где n – число молекул в единице объема. При вычислении количества молекул, долетающих до стенки, соударения молекул друг с другом можно не принимать во внимание. Это объясняется хаотичным характером движения молекул: число молекул, изменивших направление движения из-за соударений, компенсируется числом молекул, двигавшихся в других направлениях, но также участвовавших в соударениях. В соответствии с (99.2) число ударов молекул о площадку DS за единицу времени будет

равно

,

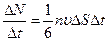а число ударов о единичную площадку DS = 1 м² за секунду

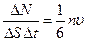. (99.3)

Суммарный импульс DК, сообщаемый элементу стенки DS за время Dt получается умножением числа ударов (99.2) на импульс (99.1), сообщаемый стенке при каждом ударе:

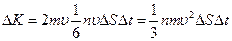
Отношение DК ко времени Dt есть сила, действующая на DS. Отношение полученной силы к площадке DS есть давление газа, оказываемое им на стенки сосуда. Следовательно,

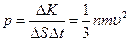
Учитывая, что e = mu ²/2 представляет собой кинетическую энергию поступательного движения молекулы, выражению для давления можно придать следующий вид:

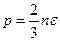(99.5)

О предположении равенства скоростей всех молекул. Пусть скорости молекул различны, причем из n молекул, содержащихся в единице объема, n ₁ молекул имеют скорости, равные u ₁, n ₂ молекул имеют скорость u ₂ и вообще n _i молекул имеют скорость u _I, то есть существует распределение молекул по скоростям. Очевидно, что

n ₁+ n ₂ +…+ n _i +…= S n _i = n

Зная распределение молекул, можно найти среднее значение скорости молекул. Для этого нужно сложить скорости всех n молекул и разделить полученный результат на n:

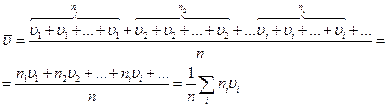(99.6)

Аналогичные рассуждения для кинетической энергии поступательного движения молекулы e, дают для среднего значения этой энергии следующее выражение:

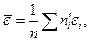(99.7)

где n ’_i – число молекул, обладающих энергией, равной e _i. Согласно (99.7) суммарная кинетическая энергия молекул, содержащихся в единице объема, равна 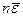– произведению числа молекул в единице объема на среднюю энергию одной молекулы, причем этот результат не зависит от конкретного вида распределения молекул по скоростям. Если молекулы каким-то образом распределены по скоростям, можно определить число ударов молекул о стенку сосуда.

Среди молекул, обладающих значением скорости u _i, имеются молекулы, движущиеся в самых различных направлениях. Поэтому можно упрощенно считать, что по направлению к элементу стенки DS движется 1/6 часть таких молекул. Следовательно, из числа молекул, имеющих скорость u _i, достигает элемента DS (рис. 222) за время Dt

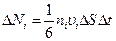(99.8)

А полное число ударов молекул любых скоростей 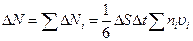При замене S n _i u _i в соответствии с (99.6) через 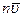число ударов об единичную площадку в единицу времени оказывается равным:

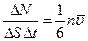. (99.9)

Это выражение отличается от полученного нами ранее (99.3) только тем, что вместо одинаковой для всех молекул скорости v в него входит средняя скорость молекул .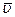

Замечание. Эта формула также является приближенной. Более строгий расчет приводит к формуле

.

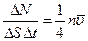Каждая из DN_i молекул (99.8) при ударе о стенку сообщает ей импульс 2 m u_i. Суммарный импульс, сообщаемый DS за время Dt молекулами всех скоростей, равен

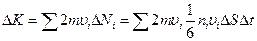
Отсюда давление равно:

,

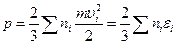где 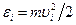– кинетическая энергия поступательного движения молекулы, имеющей скорость 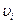. Замена в соответствии с (99.7) S n _i e _i на 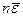дает:

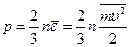(99.10)

Это выражение отличается от ранее полученного выражения (99.5) тем, что вместо одинаковой для всех молекул энергии e в него входит средняя энергия 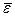. Уравнение (99.10) является основным в кинетической теории газов.

Из (99.10) следует, что при постоянном n (т. е. при неизменном объеме данной массы газа) давление пропорционально средней кинетической энергии поступательного движения молекулы 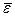. Вместе с тем температура Т, измеренная по идеальной газовой шкале, определяется как величина, пропорциональная давлению идеального газа при постоянном объеме. Отсюда следует вывод, что температура Т пропорциональна 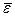. Чтобы найти коэффициент пропорциональности между абсолютной температурой Т и 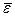, сопоставим уравнение (99.10) с уравнением состояния идеального газа (98.13). Для этого умножим уравнение (99.10) на объем киломоля V_км:

.

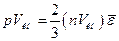Замечая, что произведение числа молекул в единице объема на объем одного киломоля равно числу Авогадро, последнее равенство можно написать в виде:

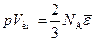
Сопоставление этого уравнения с уравнением состояния идеального газа для одного киломоля pV _км = RT показывает, что

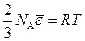
откуда

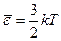(99.11)

Таким образом: абсолютная температура есть величина, пропорциональная средней энергии движения одной молекулы. Этот вывод справедлив не только для газов, но и для вещества в любом состоянии. Выражение (99.11) замечательно в том отношении, что средняя энергия 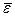зависит только от температуры и не зависит от массы молекулы. Заменив в уравнении состояния идеального газа R через N _A k и учитывая, что N_A/V_км равно n, можно получить важную формулу:

p = nkT. (99.12)

Если имеется смесь нескольких газов, разные по массе молекулы будут иметь различную среднюю скорость, но средняя энергия молекул будет одна и та же. Давление в этом случае будет равно

p = nkT = (n_l+n₂+...)kT, (99.13)

где n_l, n₂ и т. д. обозначают количество молекул первого, второго и т. д. сорта, содержащееся в единице объема. Выражение (99.13) может быть представлено в виде

p = n ₁ kT + n ₁ kT. +… Но n ₁ kT – это то давление p₁ которое было бы в сосуде, если в нем находились бы только молекулы первого сорта, n ₂ kT – то давление р₂, которое было бы при наличии в сосуде только молекул второго сорта, и т. д. Давление, обусловленное молекулами какого–либо одного сорта, при условии, что они одни присутствуют в сосуде в том количестве, в каком они содержатся в смеси, называется парциальным давлением соответствующей компоненты газовой смеси. Введя парциальные давления, на основании (99.13) можно написать, что

р = р₁+р₂+…= Sр_i. (99.14)

Таким образом, получен закон Дальтона: давление смеси идеальных газов равно сумме парциальных давлений газов, образующих смесь.

Дата добавления: 2015-05-09