Сила инерции. Принцип Д'Аламбера

НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА

Системы вытяжки костей при переломах

При сращивании сломанных костей необходимо фиксировать поврежденные участки и устранить силы, которые обычно дейст­вуют в месте перелома, до тех пор, пока он не срастется. Для этого используют различные комбинации грузов и блоков.

На рис. 7.25, а показана система вытяжки с использованием двух одинаковых грузов и двух блоков. В этом случае силы натяже­ния 7", и Г₂ равны. Те же условия можно создать и другим способом (рис. 7.25, б), используя один груз и комбинацию из подвижного и неподвижного блоков. В этом случае общая сила, действующая на ногу, равна векторной сумме двух сил натяжения (рис. 7.25, в).

9 = 20° к горизонтали. Остальные углы указаны на рисунке. При этом векторная сумма трех сил натяжения, обозначенная на рис. 7.26, б, F, имеет оптимальное направление.

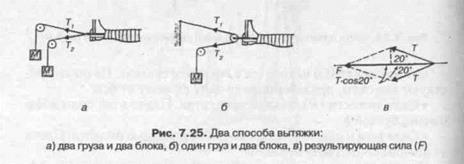
На рис. 7.26, а показана система вытяжки Рассела, применяе­мая для фиксации сломанного бедра. Эта система получена добав­лением к системе, изображенной на рис. 7.25, еще двух блоков для обеспечения связи с коленом. Бедро устанавливается под углом

Глава 8

В ряде случаев возникает необходимость описать движение, по­кой или равновесие тела, находящегося в неинерциальной систе­ме отсчета. Например, требуется выяснить какие проблемы могут возникнуть у человека, находящегося в кабине космического ко­рабля. Французский физик Д'Аламбер сформулировал простой принцип, позволяющий отвечать на вопросы о поведении тела в неинерциальной системе. Рассмотрим тело, которое находится в неинерциальной системе, движущейся относительно инерциаль-ной системы с ускорением а_с.

Векторная величина, равная произведению массы тела на уско­рение системы и направленная в сторону, противоположную ус­корению системы, называется силой инерции:

Сила инерции не является реальной силой, так как она не дей­ствует со стороны какого либо тела. Однако в неинерциальной сис­теме ее можно (и нужно!) рассматривать, как обычную силу. При этом можно «забыть» о том, что система неинерциальна.

Д'Аламбер установил, что если ко всем реальным силам (дейст­вующим со стороны других тел) добавить силу инерции, то в не­инерциальной системе можно использовать все законы и форму­лы, которые справедливы для инерциальных систем.

Пример

Пусть тело массой т подвешено на нити в кабине космического ко­рабля, который стартует с Земли и поднимается вверх с ускорением «а».

Система отсчета, связанная с таким кораблем является неинер­ционной и к ней применим принцип Д'Аламбера (ускорение сис­темы — это ускорение корабля: а_с = а). На тело действуют сила тяжести со стороны земли (mg) и сила натяжения нити (Т) (рис. 8.1). Добавим к ним силу инерции F_h = m-a, которая направле­на вниз (в сторону, обратную ускорению). Теперь можно описать по­кой тела относительно корабля: Т+ mg + F_H = 0. Учитывая направле­ния сил, получим уравнение для их величин: Т — mg — F_K = 0. Отку­да найдем натяжение нити, удерживающей тело:

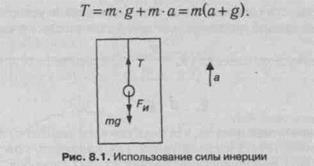
Установлено, что сила инерции неотличима от силы гравита­ции (силы тяготения). В рассматриваемом примере это означает, что никакие опыты, поставленные внутри корабля, не смогут дать ответ на вопрос, какая из ситуаций имеет место:

• либо мы находимся не в корабле, а на какой-то планете, где ускорение свободного падения равно g + a;

• либо мы движемся с ускорением g + а на космическом ко­рабле вдали от каких-либо планет (гравитационные силы отсутст­вуют);

• либо мы стартуем с Земли, поднимаясь с ускорением «а».

Во всех этих случаях результаты любого опыта будут совершен­но одинаковы.

Дата добавления: 2015-05-09