Исследование зависимости дальности полета пули от угла ее вылета

Определение коэффициента сопротивления воздуха

Так как дальность полета из-за сопротивления уменьшается в десять раз, то можно взять меньший шаг времени: 0,22с. (Шаг времени подбирают такой, чтобы отрицательных значений координаты у было в таблице немного.) А теперь в ячейке А8 подбираем такое число, при котором дальность полета составит 4км. Таким числом оказалось 0,0000038. Значит, коэффициент сопротивления воздуха для пули k = 0,0000038м².

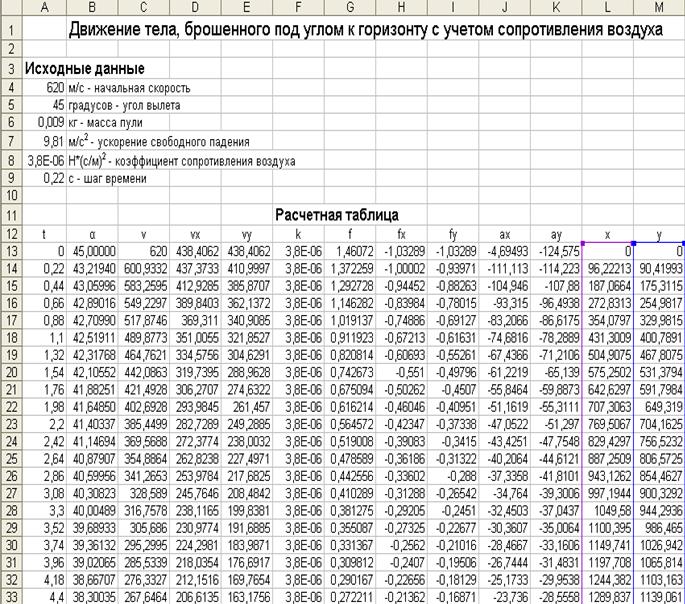
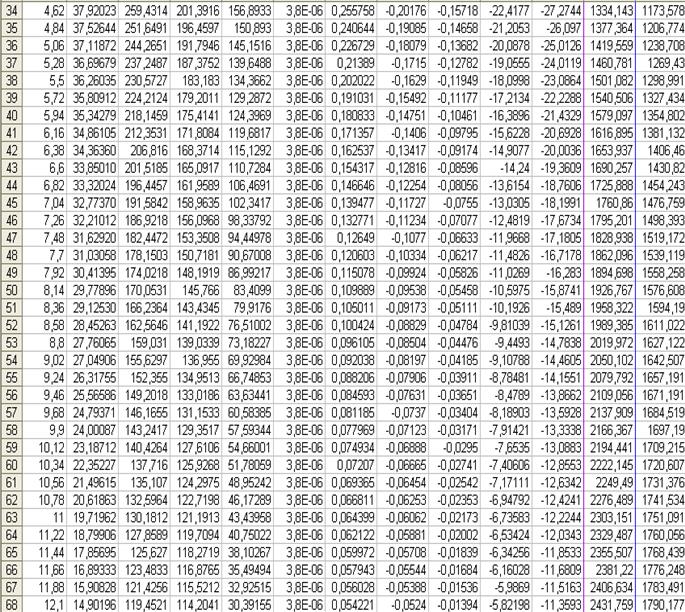
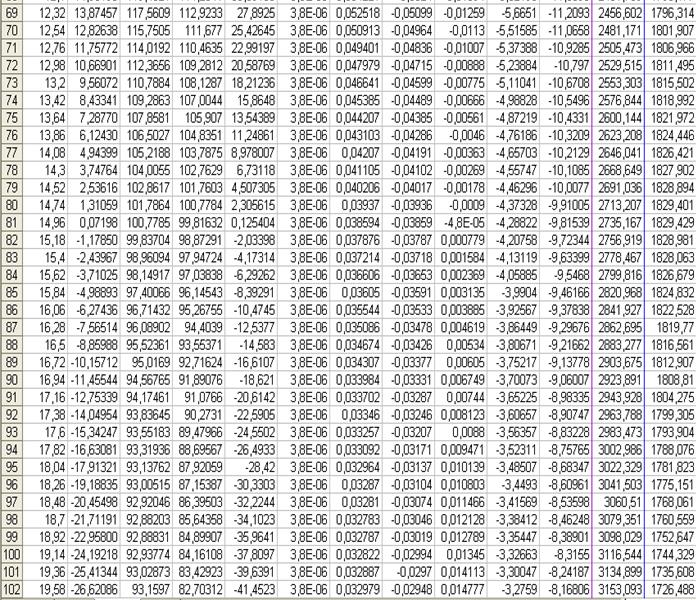
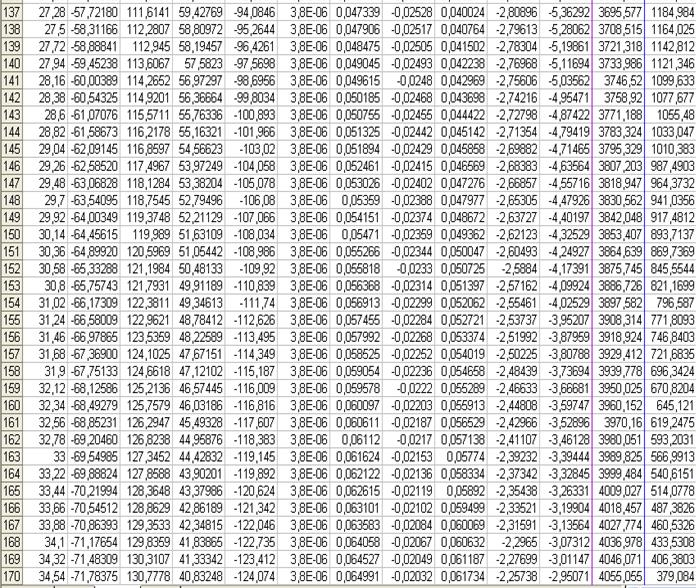
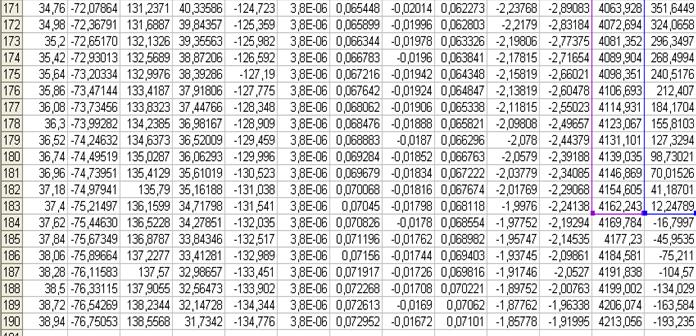
Траектория движения в этом случае будет иметь вид:

Приложение 3

В ячейке А5 подставляем значения углов: 10, 20, 30, 40, 50, 60, 70, 80 градусов и определяем для каждого угла дальность и время полета, максимальную высоту подъема пули. Результаты заносим в таблицу.

Определяем, при каком угле дальность будет максимальная.

Дальность полета и время движения при различных углах
Угол	Дальность	Высота	Время
			21,5
			28,75
			37,75
			40,25
			46,5
Уточнение максимальной дальности полета

Строим график зависимости дальности полета от угла вылета пули

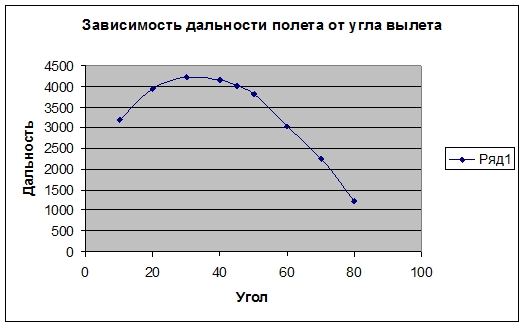
Выводы

Для углов, сумма которых равна 90°, дальность полета оказывается разной. Для меньших углов дальность полета большая, чем для больших углов. Это связано с тем, что время полета для больших углов большее и больший промежуток времени действует сила сопротивления, что и приводит к уменьшению дальности полета.

В результате той же причины расчетная дальность полета оказалась максимальной не для угла 45°, а для угла 31° и составляет 4230м.

Таким образом, с помощью компьютерной модели удалось решить все поставленные задачи.

Моделирование с помощью инструмента “Поиск решения” электронной таблицы Excel

Поиск решений является частью блока задач, который иногда называют анализ "что – если". Процедура поиска решения позволяет найти оптимальное значение формулы содержащейся в ячейке, которая называется целевой. Эта процедура работает с группой ячеек, прямо или косвенно связанных с формулой в целевой ячейке. Чтобы получить по формуле, содержащейся в целевой ячейке, заданный результат, процедура изменяет значения во влияющих ячейках. Чтобы сузить множество значений, используемых в модели, применяются ограничения. Эти ограничения могут ссылаться на другие влияющие ячейки.

Процедуру поиска решения можно использовать для определения значения влияющей ячейки, которое соответствует экстремуму зависимой ячейки – например можно изменить объем планируемого бюджета рекламы и увидеть, как это повлияет на проектируемую сумму расходов. Лабораторно-практическая работа «Задача о максимальной загрузке некоторого предприятия»

Ваше предприятие выпускает телевизоры, стерео – и акустические системы, используя общий склад комплектующих. В связи с ограниченностью запаса необходимо найти оптимальное соотношение объемов выпуска изделий. Следует учитывать уменьшение удельной прибыли при увеличении объемов производства в связи с дополнительными затратами на сбыт.

Эта модель включает данные по нескольким изделиям, в которых использованы общие комплектующие, каждому из которых соответствует своя норма прибыли. Запас комплектующих ограничен, и задача сводится к определению количества каждого вида изделий для получения наибольшей прибыли.

Решите задачу, используя инструмент Поиск решения.

1. Создайте таблицу по образцу:

	A	B	C	D	E	F
		Структура производства с уменьшением нормы прибыли
				Телевизор	Стерео	Ак.система
			Количество->
	Наименование комплектующих	Склад	Использованные
	Шасси
	Кинескоп
	Динамик
	Блок питания
	Электронная плата

2. В ячейку С5 поместите формулу, которая будет подсчитывать количество использованных комплектующих для всех видов изделий. Количество изделий зафиксируйте. Скопируйте формулу в диапазон С6:С9.

3. В ячейку Н9 введите значение уменьшения коэффициента отдачи – 0,9.

4. Подготовьте таблицу результатов:

	C	D	E	F
		Прибыль:
	По видам изделий	7 220р.	5 887р.	1 811р.
	Всего	14 917р.

5. В ячейки D13, E13, F13 поместите формулы, определяющие прибыль по видам изделий с учетом уменьшениякоэффициента отдачи соответственно: =75*МАКС(D3;0)^$H$9; =50*МАКС(E3;0)^$H$9; =35*МАКС(F3;0)^$H$9.

6. В ячейку D14 поместите формулу, подсчитывающую общую прибыль.

7. Сделайте активной ячейку D14, выполните команду Сервис/Поиск решения, и используя данные следующей таблицы определите количество выпускаемых изделий и максимальную прибыль.

Параметры задачи
Результат		D14		Цель - получение наибольшей прибыли.
Изменяемые данные	D3:F3		Количество выпускаемых изделий каждого вида.
Ограничения		C5:C9<=B5:B9	Количество использованных комплектующих не должно превышать
				их запаса на складе.
		D3:F3>=0		Количество выпускаемых изделий должно быть больше 0.

8. Изменение H9 на 1,0 (если прибыль не зависит от объема производства) и повторно запустите процесс поиска решения, найденное ранее оптимальное решение будет другим.

9.Постройте диаграмму, отражающую количество имеющихся и использованных комплектующих.

Дата добавления: 2015-05-09