Показникова функція, її графік і властивості

Через три точки, які не лежать на одній прямій, можна провести площину, і до того ж тільки одну.

Теорема.

Теорема про існування площини, яка проходить через три точки

Б-2 Існування площини, яка проходить через три дані точки.

Нам відомо два способи задання площини: площину можна провести через дві прямі, які перетинаються, а також через пряму і точку, яка не належить цій прямій.

Існує третій спосіб.

Студенти самостійно знайомляться з доведенням цієї теореми за підручником (с. 6).

Слід звернути увагу студентів на те, що площина однозначно задається трьома точками, які не лежать на одній прямій, і тому в літературі площину, яка проходить через точки А, В, С і С АВ, позначають символом (АВС).

Функція виду у = а^х, де а > 0, а ≠ 1, називається показниковою (з основою а).

1. Область визначення показникової функції — множина R дійс­них чисел, бо степінь a^х, де а > 0, визначений для всіх х 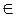R.

2. Множина значень показникової функції — множина всіх до­датних дійсних чисел

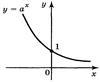
3. Показникова функція у = a^х є зростаючою на множині дійсних чисел, якщо а > 1, і спадною, якщо 0 < а < 1.

4. Якщо х = 0, то у = а° = 1.

5. Якщо х > 0, то у > 1, якщо а > 1, і у < 1, якщо 0 < а < 1.

6. Якщо х < 0, то у < 1, якщо а > 1, і у > 1, якщо 0 < а < 1.

7. Графіком показникової функції є крива, яка називається екс­понентою.

Властивості показникової функції записати в робочому зошиті у вигляді таблиці

Показникова функція у = а^х, а > 0, а ≠ 1
а > 1	0 < а < 1
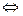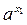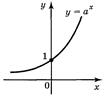
1. D(y) = R 2. Е(у) = (0; + ) 3. Зростає x 1 > x 2 > 4. Якщо х = 0, то у = 1 5. Якщо х < 0,то у < 1 6. Якщо х > 0, то у > 1	1. D(y) = R 2. E(y) = (0; + ). 3. Спадає x 1 > x 2 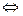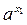< 4. Якщо х = 0, то у = 1 5. Якщо х < 0, то у > 1 6. Якщо х > 0, то у < 1

Б-3 Взаємне розміщення двох прямих у просторі. Паралельність прямих. Мимобіжність прямих

Прямі, які не перетинаються і лежать в одній площині, називають паралельними, а дві прямі, які не перетинаються і не лежать в одній площині, називають мимобіжними.

Випадки взаємного розташування двох прямих у просторі демонструються за допомогою стереометричного набору або на каркасній моделі куба.

Отже, дві прямі а і b у просторі можуть: перетинатися, бути паралельними, бути мимобіжними.

Теорема про існування і єдиність прямої, яка проходить через дану точку і паралельна даній прямій.

З аксіоми паралельності Евкліда випливає, що в площині через дану точку можна провести не більше однієї прямої, яка паралельна даній прямій. А скільки таких прямих можна провести у просторі?

Нехай дано пряму a і точку А, що не лежить на ній. Через них можна провести єдину площину (теорема 1.1). У цій площині можна провести єдину пряму b, яка паралельна прямій α (рис. 33).

Отже, у просторі через дану точку А можна провести єдину пряму, паралельну даній прямій а.

Дата добавления: 2015-05-09