Решение задач с использованием формул

Исследование одной задачи парной регрессии

Используя условные данные таблицы №1, построим следующие регрессионные модели с полным исследованием и анализом их значимости, адекватности, качества и точности:

1) Линейная модель ŷ=a+bx,

2) Степенная модель ŷ=a+b√x,

3) Степенная модель ŷ=a+bx^2,

4) Гиперболическая модель ŷ=a+b/x,

5) Полулогарифмическая модель ŷ=a+blnx.

Массив наблюдений состоит из 25 наблюдений. Прогнозное значение будем рассчитать, например, для х=12 млрд. рубл. (данные условные).

Таблица № 1

№ наблюдения	Значения Y (расходы на одежду, млрд. рубл.)	Значения X (располагаемый доход, млрд. рубл.)
1.	0,363	4,80
2.	0,366	4,90
3.	0,373	5,04
4.	0,396	5,42
5.	0,426	5,81
6.	0,442	6,16
7.	0,469	6,47
8.	0,490	7,01
9.	0,500	7,23
10.	0,494	7,52
11.	0,518	7,79
12.	0,554	8,10
13.	0,593	8,65
14.	0,587	8,58
15.	0,609	8,76
16.	0,638	9,07
17.	0,675	9,43
18.	0,736	9,89
19.	0,767	10,16
20.	0,779	10,22
21.	0,826	10,49
22.	0,842	10,58
23.	0,885	10,95
24.	0,901	11,22
25.	0,943	11,61

Примечания:

1. При проведении процедуры линеаризации для гиперболической модели t=1/x будем учитывать 5 цифр после запятой.

2. После проведения эконометрического моделирования в конце работы изложен общий вывод по исследованию в целом, содержащий экономическую и эконометрическую составляющие, не считая отдельные выводы по моделям.

3. Расчёты по данным таблицы будем выполнять в двух вариантах: вручную и в Приложении Excel.

РЕШЕНИЕ:

1.1.1Параметры a и b линейной регрессии рассчитываются с помощью метода наименьших квадратов. По исходным данным определим , , , , 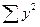и их средние значения (см. в расчетной таблице 1).

Для построения рабочей таблицы 1 и расчетов по формулам вводим данные в Excel (просто для облегчения ручных расчетов: это не компьютерное решение):

Таблица 1. Ввод данных наблюдения.

Рис. 1. Ввод данных и вычисление сумм и средних по столбцам.

Система нормальных уравнений (получаемая методом наименьших квадратов):

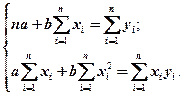(1)

Для моей задачи система (1) примет вид:

Методом Крамера получаем решение системы: a = - 0,0853; b = 0,08406.

Уравнение линейной регрессии имеет вид:

.

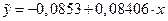Параметры уравнения можно определить и по следующим формулам:

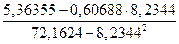= = 0,0840607;

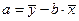= = - 0,0853094;

Величина коэффициента регрессии b = 0,08406 означает, что с ростом располагаемых доходов на 1 млрд. руб. расходы на одежду увеличится в среднем на 0,08406 раз.

Отрицательное значение свободного члена a = -0,0853 может означать, что расходы на одежду отсутствуют при малых доходах.

По полученному уравнению регрессии рассчитаем расчетные величины расходов , а также отклонение расчетной величины от фактически наблюдаемой величины расходов . Рассчитанными величинами заполним новые столбцы таблицы 1.

Таблица 1 Расчет показателей парной линейной регрессии и корреляции

1.1.2. Коэффициент эластичности ( Y по Х) показывает, на сколько процентов (от средней) изменится в среднем 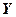при увеличении только Х на 1%.

Средний коэффициент эластичности для линейной регрессии находится по формуле:

= 0,08406*(8,2344/0,60688)=1,14056;

1.1.3. По данным табл. 1 оценим на уровне значимость уравнения регрессии 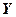по .

Оценить значимость уравнения регрессии – означает установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных для описания зависимой переменной.

выборочная дисперсия зависимой переменной регрессии равна сумме объясненной дисперсии зависимой переменной и необъясненной дисперсии зависимой переменной:

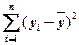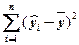= + (2)

или же через обозначения:

, ( = + ), (3)

где 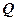- общая сумма квадратов отклонений ( - Total Sum of Squares) зависимой переменной от своего выборочного среднего . - объясненная сумма квадратов отклонений (обусловленная уравнением регрессии) ( - Explained Sum of Squares), другими словами, объясненная дисперсия зависимой переменной. - необъясненная (остаточная) сумма квадратов отклонений ( - Residue Sum of Squares) всех наблюдений, т.е. необъясненная дисперсия зависимой переменной или по-другому – выборочная дисперсия остатков в наблюдениях.

Суммарной мерой общего качества уравнения регрессии является коэффициент детерминации - это доля объясненной дисперсии в общей дисперсии, т.е.

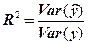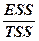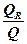= = = = = . (4)

Величина показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной. является мерой качества, как говорят, подгонки регрессионной модели к наблюдаемым значениям. Так как , то .Чем ближе к единице, тем больше доля объясненной дисперсии в общей дисперсии и тем лучше регрессия аппроксимирует эмпирические данные, т.е. тем теснее наблюдения примыкают к линии регрессии.

= = 0,95958, показывает достаточно высокое качество уравнения регрессии: примерно 95,958% наблюдений объясняются уравнением регрессии.

1.1.4. Проведем 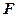- тест Фишера на качество оценивания парной

Дата добавления: 2015-05-09