Нелинейные модели регрессии и их линеаризация

2) СТЕПЕННАЯ МОДЕЛЬ 1.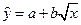

Можем столбец наблюдении Х взять под корень и задачу свести к предыдущей задаче. Аналогично применяем пакет анализа Excel и строим регрессию.

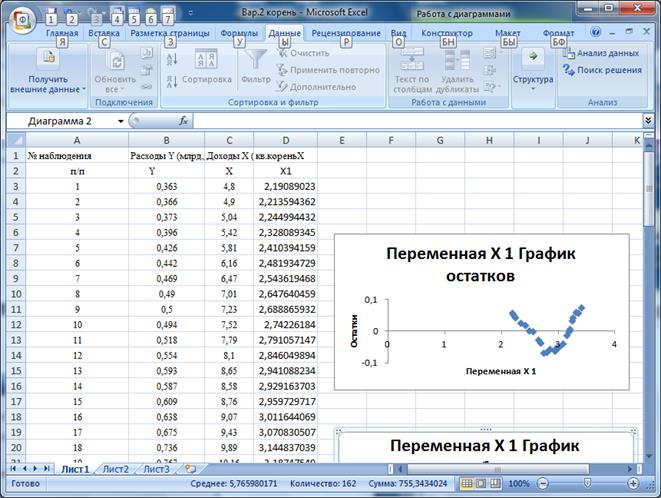
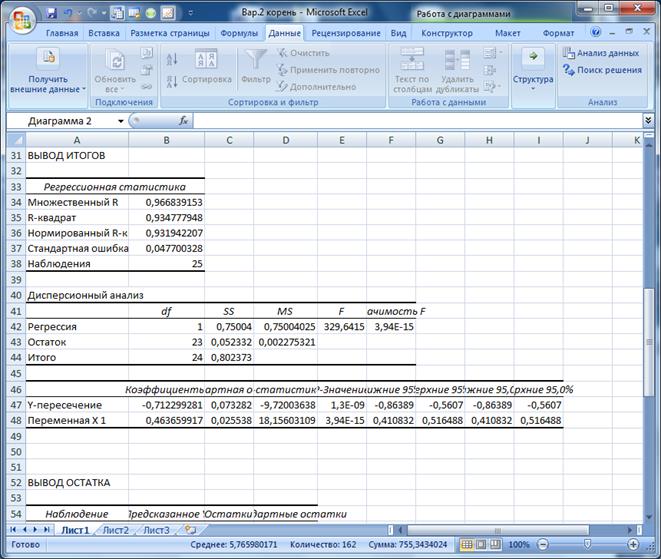
Рисунок 8 Результаты расчета параметров степенной функции 1.

Таким образом, уравнение регрессии имеет вид:

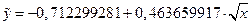
Параметр b= 0,46366имеет порядок коэффициента эластичности, который показывает, что с ростом величины доходов на 1% ожидаемый расход увеличится в среднем на 0,46366%.

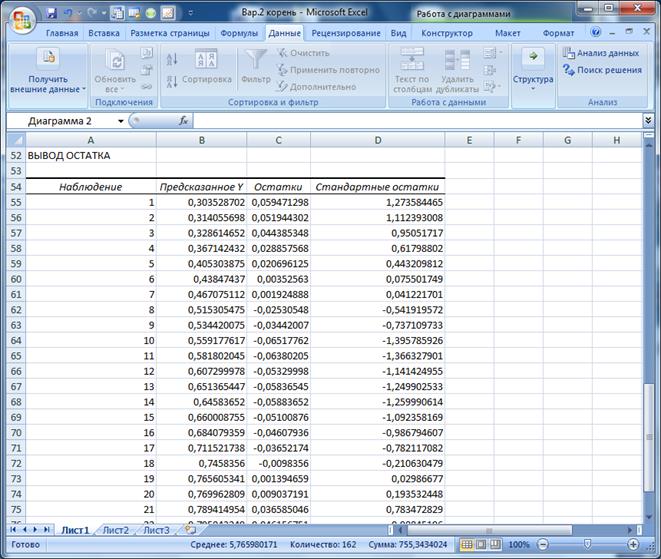
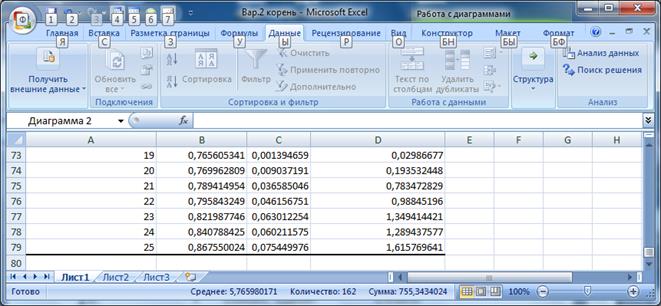
3) СТЕПЕННАЯ МОДЕЛЬ 2.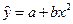

Можем столбец наблюдении Х возвести в квадрат и задачу свести к пераой задаче парной линейной регрессии. Аналогично применяем пакет анализа Excel и строим регрессию.

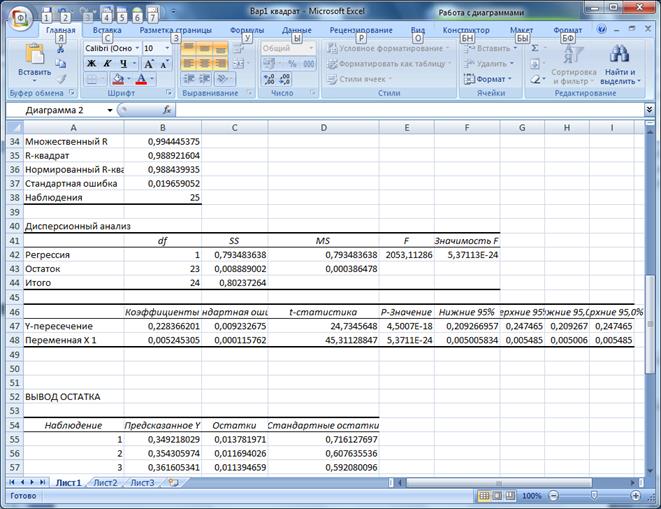
Рисунок 9 Результаты расчета параметров степенной функции 2.

Таким образом, уравнение регрессии имеет вид:

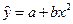= 0,228366201 + 0,005245305

Параметр b= 0,005245имеет смысл схожее с коэффициентом эластичности, и показывает, что с ростом величины доходов на 1% общий расход увеличится в среднем на 0,52%.

4) ГИПЕРБОЛИЧЕСКАЯ МОДЕЛЬ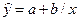

Регрессия в виде равносторонней гиперболы имеет вид: 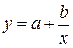, чтобы оценить параметры a и b, привожу модель к линейному виду, заменив 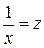. Тогда 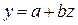. Результаты замены представлены на рисунке 11.

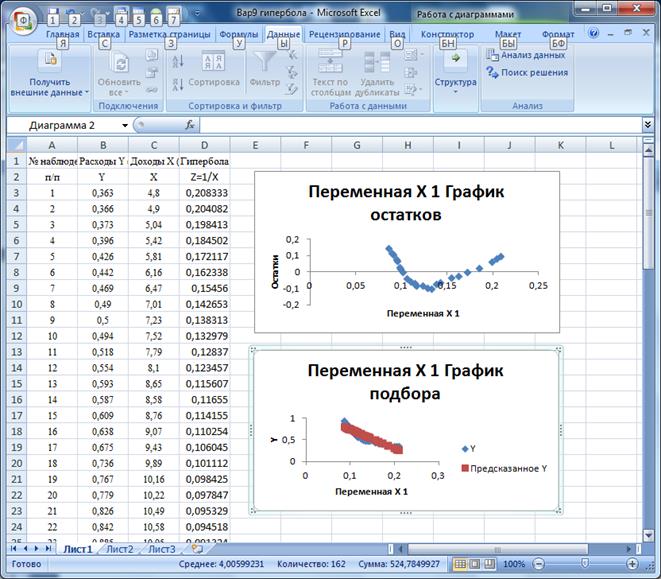
Рис. 11. Замена переменной Z = 1/X.

Рис. 12. Обращение к анализу «Регрессия»

Далее с помощью инструмента Регрессия рассчитываю параметры уравнения. Результаты расчета представлены на рисунке 13.

Рис. 13. Результаты анализа с помощью инструмента «Регрессия».

Таким образом, уравнение регрессии имеет вид:

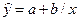= 1,176672135 – 4,360822739/ х

Параметр b= - 4,360822739, как и коэффициент эластичности, показывает, что с ростом величины Z (фактически с уменьшением доходов) на 1% общий расход уменьшится в среднем на 4,3608%.

Дата добавления: 2015-05-09