Майбутня вартість грошових потоків

Джерела інформації для проведення фінансового аналізу.

При плануванні грошових надходжень у розрахунках за опе­раціями на фінансовому ринку необхідно враховувати фактор часу. Він відіграє не менш важливу роль, ніж обсяги грошових коштів. Це зумовлено нерівноцінністю грошей, які відносять до різних моментів часу, тобто вартість гривні сьогодні більша, ніж вартість гривні, отриманої завтра або через певний час.

Різниця у вартості грошей зумовлена дією декількох факторів, до яких відносять інфляцію або знецінення грошей. Окрім того, теоретично будь-яка сума грошей може бути інвестована і приноситиме дохід. Тому не отримані сьогодні гроші слід враховувати як невикористані можливості в отриманні доходу в майбутньому. В ринкових умовах необхідно враховувати фактор ризику, адже невизначеність майбутнього зменшує вартість грошей, які можуть бути отримані через певний час.

На вартість грошей впливає схильність до ліквідності з боку інвесторів. Це проявляється в тому, що перевага завжди надаєть­ся грошам, які можна отримати сьогодні й задовольнити свої по­треби. Тому, якщо інвестори вкладають свої кошти в проекти, то чекають на винагороду, тобто високі доходи у майбутньому як компенсацію за втрату ліквідності.

Гроші, які інвестуються в проекти, можуть принести значний дохід, але можуть і втратити свою вартість внаслідок ризику, інфляції. Тому підприємства, кредитори хочуть знати майбутню вартість грошей або сьогоднішню вартість майбутніх доходів з урахуванням ризику.

Різноманітність задач щодо визначення зміни вартості грошей в часі можна звести у такі групи:

І. Компаундирування - визначення майбутньої вартості грошей. (FV, future value - майбутня вартість, англ.):

1.1. вкладених водночас на певний термін під певний % (просте компаундирування);

1.2. вкладених рівними частками через рівні проміжки часу під певний % - це визначення FV анюїтетів або ренти:

1.2.1. компаундирування звичайної (відстроченної) ренти - це визначення FV ренти, вклади по якій проводяться в кінці кожного періоду;

1.2.2. компаундирування вексельної ренти - визначення FV ренти, вклади по якій проводяться на початку кожного періоду.

ІІ. Дисконтування - визначення поточної (теперішньої) вартості грошей (PV, present value - теперішня вартість, англ.):

2.1. отримуємих в майбутньому водночас (просте дисконтування);

2.2. отримуємих в майбутньому через рівні проміжки часу:

2.2.1. в кінці кожного періоду – це визначення теперішньої вартості звичайних анюїтетів, або PV звичайної (відстроченної) ренти;

2.2.2. на початку кожного періоду - це визначення PV вексельної ренти.

Розглянемо детальніше сутність та особливості визначення теперішньої та майбутньої вартості грошей та грошових потоків.

1. Майбутня вартість грошей та її визначення.

1.1.Просте компаундирування.

Компаундирування - процес переходу від теперішньої вартості (PV) до майбутньої (FV). Майбутню вартість грошей можна визначити при нарахуванні простих і складних відсотків.

** Простий відсоток – це нарахування відсотку лише на початкове інвестовану суму.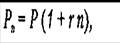

де Р_n – майбутня вартість; P – сьогоднішня вартість; r – відсоток; n – кількість років

Приклад 1.

Розрахуйте нарощену суму з вихідної суми в 20000 грн. при розміщенні її в банку на умовах нарахування простих відсотків, якщо річна ставка 15%, а період врахування – 10 років.

Нарощена сума складає:

** Складний відсоток - може нараховуватися один або декілька разів на рік.

* нарахування відсотку один раз на рік. У довгострокових фінансово–кредитних угодах частіше використовують нарахування складних відсотків. При нарахуванні складних відсотків їх нараховують не тільки на основну суму, а й на суму, що включає як основну суму, так і нараховані раніше відсотки. У цьому випадку кажуть, що відбувається капіталізація відсотків в міру їх нарахування.

Приклад 2.

Підприємець хоче покласти на депозит в банк 100 гр.одиниць одноразово під 5% річних на 5 років. Яку суму грошей матиме підприємець наприкінці першого року і який буде результат через 5 років?

PV = 100 гр.одиниць

і = 0,05.

I= 100 гр.од. х 0, 05 = 5 гр.од. - грошовий вираз відсотка, який отримає підприємець наприкінці 1 року.

n = 1; n = 5.

Таким чином, для n = 1:

FVn = FV₁ = PV + I = PV + PV(r) = PV (1+ r) = 100 гр.од. х (1 + 0,05) = 100 гр. од. х (1,05) = 105 гр.од.

Тобто наприкінці першого року підприємець матиме 105 гр.одиниць. Підприємець заробив за перший рік 100 гр.од. х 0,05 = 5 гр.од, тому по закінченні першого року сума внеску дорівнювала вже 100 гр.од + 5 гр.од. = 105 гр.од.

Другий рік почався вже з цієї суми, відсоток склав 5,25 гр.од.. Відсоток за другий рік більше відсотку за перший тому, що підприємець заробив вже відсоток на відсоток першого року внеску: 5 гр.од. х 0,05 = 0,25 гр.од. Цей процес продовжується, і внаслідок того, що кожного разу початкова сума вище попередньої, річний відсоток виростає. Загальний зароблений відсоток 5,00+5,25+5,51+5,79+6,08=27,63 гр.од.,

Вартість наприкінці 2 року:

FV₂ = FV₁ (1+ r) = PV (1+ r)(1+ r) = PV (1+ r)² = 100 гр.од. х (1,05)² = 110,25гр.од.

Кінцевий результат третього року внеску: FV₃= FV₂ (1+ r) = PV(1+r)³ = 100 гр.од х (1,05)³ = 115,76 гр.од.

Таким чином, FV₅ = 100 гр.од. х (1,05)⁵ = 127,63 гр.од.

Всі ці розрахунки можна звести до вищевикладеного рівняння:

FVn= PV (1+ r)ⁿ,

*Нарахування відсотків декілька разів на рік. Складний відсоток може нараховуватися частіше, ніж один раз на рік, наприклад, раз в півроку, квартал, місяць тощо. Як правило, у фінансових контрактах фіксується річна відсоткова ставка і при цьому відсотки можуть нараховуватися по півріччях, кварталах, місяцях тощо. Відсотки, що нараховуються з певною періодичністю, називаються дискретними. В цьому випадку річна ставка називається номінальною, а відсоткова ставка за один інтервал нарахування вважається рівною відношенню номінальної ставки до кількості інтервалів в році. Нарощена сума буде розраховуватись за наступною формулою (формула 4.11):

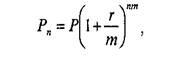
де m — періодичність нарахування відсотку протягом року.

Приклад 3.

На вклад до банку в розмірі 9000 грн. строком на 5 років банк нараховує 18% річних. Яка сума буде на рахунку в кінці строку, якщо нарахування відсотків здійснюється за схемою складних відсотків: а) щопівроку; б) щоквартально?

Дата добавления: 2015-05-07