Призмою називається многогранник, у якого дві грані, – рівні многокутники з відповідно паралельними сторонами, а всі інші грані – паралелограми». 1 страница

Создание запросов

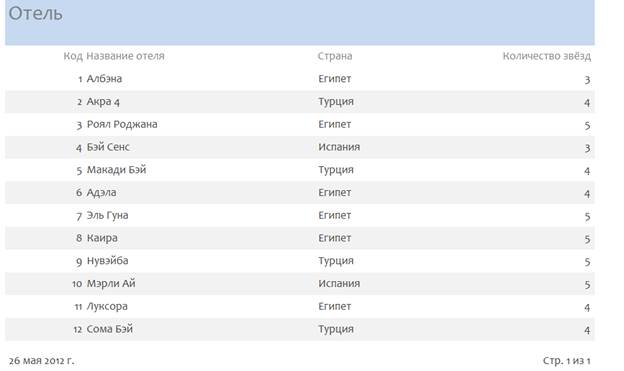
При создании запросов использовался мастер запросов. Были созданы запросы.

1.Запрос на отбор 4-звёздочного отеля.

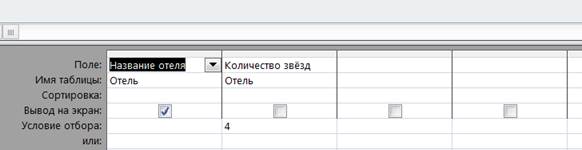
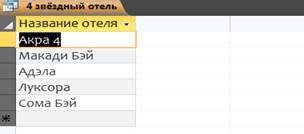
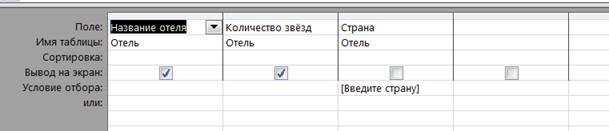
2.Запоросы с параметром.

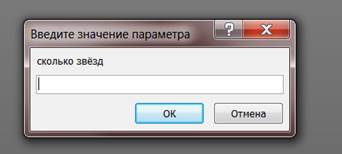
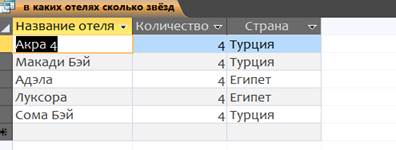
Или в какой стране какие отели:

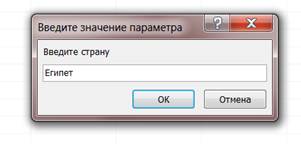
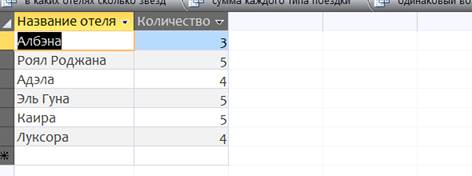
3.Запросы на вычисление.

Посчитать полную сумму каждого типа поездки.

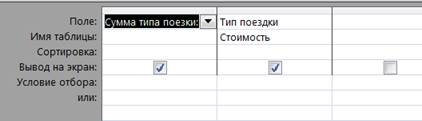
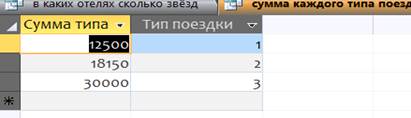
4.Запросы с условием отбора

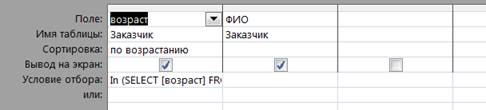
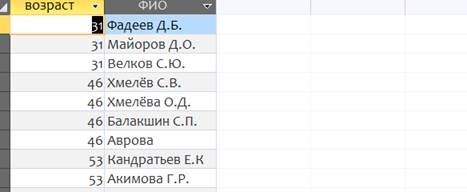
Или одинаковый отель:

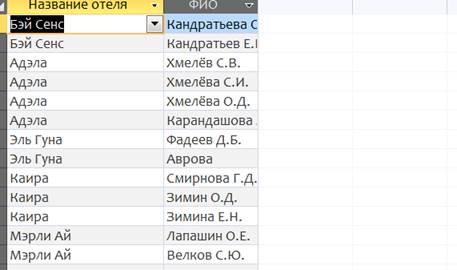
6.Создание отчётов

Отчеты создавались при помощи мастера отчетов.

Зразок відповіді. В означенні не названі всі необхідні видові ознаки. Даному означенню задовольняють не лише призми, але й інші многогранники, відмінні від призм (рис.1). Означення є занадто широким, зміст поняття збіднений, перерахованих у означенні видових ознак недостатньо для означення.

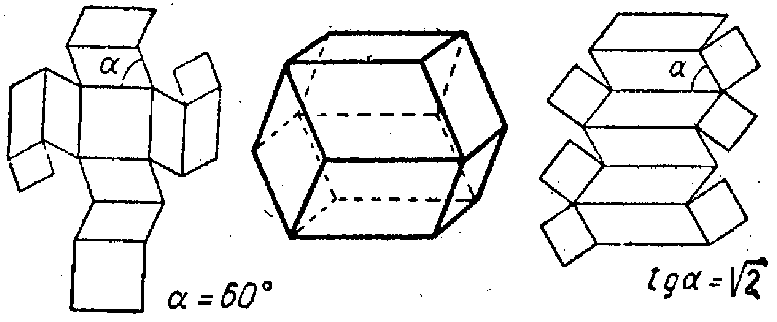
Рис. 1. Многогранники

ЕВРИСТИКИ І ПОШУК РОЗВ'ЯЗАННЯ

У процесі роботи з математичними поняттями слід звернути увагу на використання евристичних прийомів загального виду [9], а саме класифікація, обмеження, узагальнення тощо.

КЛАСИФІКАЦІЯ

Класифікація є одним із видів поділу.

У зв'язку з тим, що відмінність поділу від класифікації у навчанні шкільної ма­тематики не має суттєвого значення, немає потреби чинити відмінність між ними.

Задача 9. Запропонуйте поділ поняття «паралелограм».

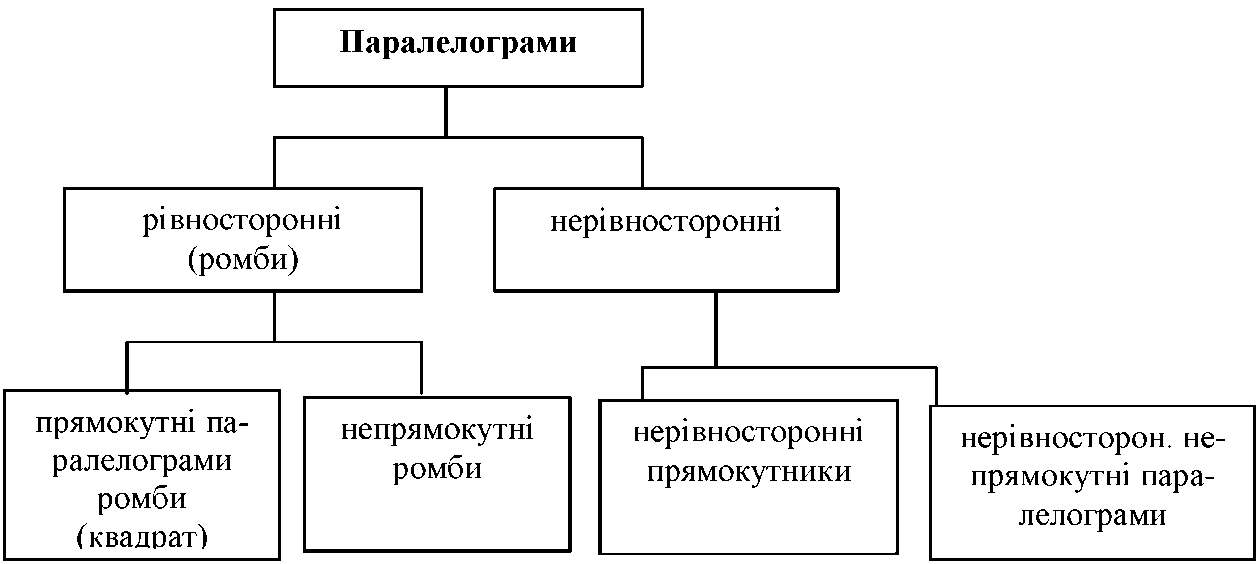
Рис. 2. Класифікація поняття «паралелограм»

Зразок відповіді. Поняття «паралелограм» можна класифікувати за допомогою схеми (див. рис. 2) з переліком членів поділу: спочатку за основу класифікації обрано рівність сторін, по друге - основою класифікації послужила градусна міра кутів паралелограму.

Схематично співвідношення між родовим і видовим поняттями можна зобразити, наприклад, у вигляді схеми Ейлера-Венна (рис. 3).

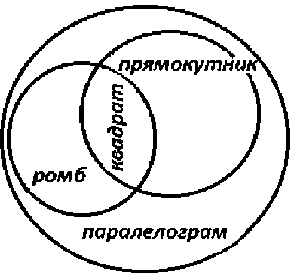
Рис. 3. Класифікація поняття паралелограм"у вигляді схеми Ейлера-Венна

Задача 10. Перевірте, чи правильно виконана дія ділення поняття. Якщо так, за якою основою виконано ділення?

а) прямокутники можуть бути рівносторонні та нерівносторонні;

б) трикутники діляться на різносторонні, рівнобедрені та рівносторонні;

в) чотирикутники діляться на прямокутники, ромби та квадрати;

г) трикутники можуть бути правильні, гострокутні, тупокутні, рівносторонні;

д) раціональні числа бувають додатні та від'ємні;

є) функції бувають парні, непарні, загального виду;

ж) трапеція може бути рівнобічна, прямокутна;

з) піраміда ділиться на повні піраміди та зрізані.
Зразок відповіді.

а). Рівносторонні та нерівносторонні прямокутники знаходяться у відношенні протилежності, за основу ділення було взято довжина сторін.

б), в). Не виконується вимога про те, що члени ділення повинні виключати один одного. Для пункту б) перераховані види трикутників не виключають один одне, рівносторонній трикутник є одночасно рівнобедреним. Для пункту в) квадрат одночасно є і ромбом, і прямокутником.

г), ж). Не виконується вимога, про те, що ділення повинно мати одну основу. Основою служать дві ознаки: градусна міра кутів та довжина сторін.

д, є), з). Не виконується вимога, про те, що ділення повинно бути помірним, тобто обсяг поняття що ділиться, повинен дорівнювати сумі обсягів понять, які є членами ділення. У випадку д) пропущений один член ділення – нуль. У випадку є) пропущений один член ділення – функція у = 0 (і парна і непарна одночасно). У випадку з) сума обсягів понять повної піраміди та зрізаної піраміди більша від обсягу діленого (зрізана піраміда не є видом піраміди).

Задача 11. Запропонуйте класифікацію чисел, що вивчаються у загальноосвітній школі.

Зразок відповіді.

Така класифікація може бути представлена схемою, зображеною на рис. 4.

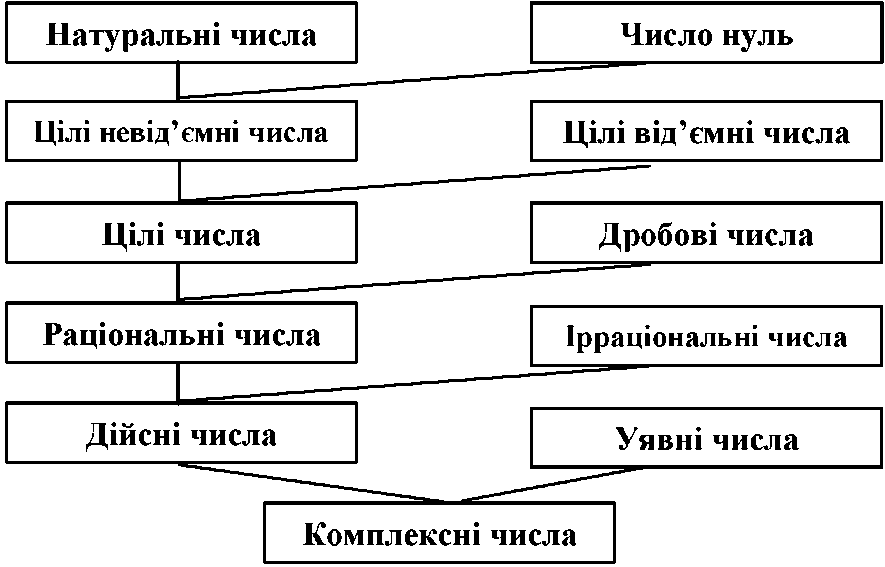
Рис. 4. Класифікація чисел

Варто пам'ятати:

1) класифікація повинна проводитися лише за однією основою;

2) ієрархічна класифікація має бути лише безперервною (без пропусків рів­нів ділення);

3) сума обсягів видових понять повинна збігатися з обсягом родового поняття (вимога повноти класифікації);

4) отримані підкласи повинні виключати один одного.

Задача 12. Запропонуйте класифікацію понять «паралелограм» та «трикутник» за двома ознаками – за сторонами та кутами.

Зразок відповіді.

На рис. 5 проілюстрована класифікація поняття «паралелограм», а на рис. 6 поняття «трикутник».

За сторонами   За кутами	нерівносторонній	рівносторонній
нерівнокутний
рівнокутний

Рис. 5. Класифікація паралелограмів

За кутами   За сторонами	гострокутний	прямокутний	тупокутний
різносторонній
рівнобедренний
рівносторонній

Рис. 6. Класифікація трикутників

Коли краще ознайомити учнів із класифікацією, до чи після вивчення відповідної теми?

Перш за все, потрібно мати на увазі, що прийнятий порядок викладу (матеріалу) не завжди дозволяє зробити вибір. Класифікація може зажадати знання додаткового кола теорем, у цьому випадку проведення класифікації перед вивченням теми буде передчасним, не будучи підсумком попередніх теорем і означень, не підкріплена логічними міркуваннями, така класифікація не представляє цінності.

У тих випадках, де можливо, слід починати вивчення теми з класифікації, це може внести стрункість до викладу матеріалу і, отже, полегшити розуміння учнями питань, що розбираються.

Користь класифікації у викладанні математики недооцінюється. Можливості вживання класифікації повністю не використовуються.

Недостатнє широке вживання класифікації понять, що вивчаються, приводить до відсутності системи в знаннях учнів, бо систематичність знань нерозривно пов'язана з вимогою встановлення зв'язку між поняттями.

ОБМЕЖЕННЯ

Обмеженням поняття називається перехід від понять більшого об'єму (більш загальних) до понять меншого об'єму (менш загальних).

Задача 13. Здійсніть обмеження поняття «чотирикутник».

Зразок відповіді. Розглянемо вид перетину правильного тетраедра площиною Р, що проходить через середини ребер МА і МВ паралельно ребру МС (рис. 7). Площина Р перетинає всі чотири грані тетраедра, отже, в перерізі – чотирикутник. Потім, довівши, що сторонами отриманого чотирикутника є середні лінії трикутників – граней тетраедра, робимо висновок: чотирикутник є ромбом. Нарешті, показавши перпендикулярність суміжних сторін ромба, приходимо до остаточного висновку: шуканий переріз – квадрат. Відносно шуканого перетину були зроблені твердження:

1) переріз - чотирикутник;

2) переріз - ромб;

3) переріз - квадрат.

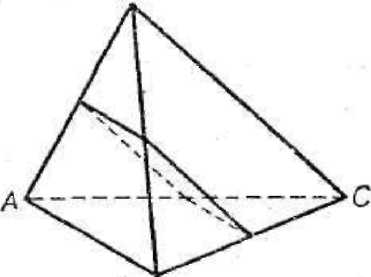
Рис. 7. Переріз тетраедра

Обмежити поняття можна додаванням до ознак, що складають зміст поняття, окремої ознаки обмежуваного поняття. Окрема ознака обмежуваного поняття є ознака, що відноситься лише до частини об'єктів, які входять в обсяг поняття. Це правило є простим наслідком закону «зворотного відношення».

Обмеження поняття не можна змішувати з уявним розчленуванням (діленням на частини) предмету. Наприклад, якщо перейдемо від поняття «ламана» до поняття «ланка ламаною», ми не обмежимо поняття ламаною, а просто здійснено ділення останньої на частини.

Під час перевірки правильності проведеного обмеження поняття інколи поступають таким чином: перед назвою обмежуваного поняття (А) ставлять назву поняття, отриманого у результаті обмеження (В), і на початку додають слово «всякий» (або «всяка»). Якщо отримане таким чином речення ви­явиться правильним (всякий квадрат – ромб), то обмеження (ромб – квадрат) проведене правильно, інакше (всяка ланка ламаною – ламана) обмеження (ламана – ланка ламаною) проведене неправильно.

Задача 14. Перевірте, чи правильно обмежені поняття: паралелограм – ромб; конус – основа конуса.

Зразок відповіді. Усякий ромб є паралелограмом. Усяка основа конуса є конусом. У першому випадку обмеження здійснено правильно, у другому – неправильно: основа конуса є елемент конуса, а не вид конуса.

УЗАГАЛЬНЕННЯ

Узагальнення поняття - логічна операція, зворотна обмеженню. При узагальненні поняття ми переходимо від понять меншого об'єму (менш загальних) до понять більшого об'єму (більш загальних).

Задача 15. Здійсніть узагальнення поняття «квадрат» і покажіть зв'язок узагальнення з обмеженням.

Зразок відповіді. Узагальнення поняття «квадрат» і зв'язок узагальнення з обмеженням надано у схемі 1.

УЗАГАЛЬНЕННЯ		Квадрат		ОБМЕЖЕННЯ
	Прямокутник
	Паралелограм
	Опуклий чотирикутник
	Опуклий многокутник
	Плоский многокутник
	Многокутник

Схема 1. Зв'язок між узагальненням та обмеженням

Щоб полегшити розв'язання поставленої задачі, інколи варто починати з розгляду окремого випадку (з розгляду аналогічної задачі), для чого замість поняття А беремо поняття В меншого обсягу. Отриманий результат при розв'язанні часткової задачі може дати засоби для розв'язання задачі у загальному вигляді. Може знадобитися декілька подібних переходів від розв'язання менш загальних задач до задач більш загальних, перш ніж прийдемо до розв'язання поставленої задачі. Прикладом може служити обчислення обсягу поняття паралелепіпед. Спочатку розглядається прямокутний паралелепіпед, потім прямий паралелепіпед і вже потім паралелепіпед узагалі.

Узагальнення поняття відбувається шляхом відкидання основних ознак поняття, тобто ознак, що належать всім об'єктам, що входять в обсяг узагальнюваного поняття. При невиконанні цієї умови може вийти уявне з'єднання предметів, а не узагальнення поняття, що ми маємо, наприклад, при переході від поняття «напівпряма» до поняття «пряма». Щоб перевірити, чи правильно здійснено узагальнення поняття, можна розглянути речення «всяке («всякий», «всяка») В є А, де В – початкове поняття, а А – поняття, що отримане у результаті узагальнення. У разі справедливості (помилковості) речення узагальнення здійснено правильно (неправильно). Оскільки не можна сказати, що усяка напівпряма є пряма, то узагальнення «напівпряма» – «пряма» помилкове [8, с.21-22].

БЛОК ІІІ. Завдання для самоконтролю

1. Які поняття використовуються в означенні паралелограма?

2.Як у геометрії зазвичай установлюється, що об'єкт, що задовольняє сформульованому означенню, дійсно існує? (Наведіть відповідні приклади).

3. Наведіть приклади математичних понять, які виражаються одним, двома, трьома, чотирма словами.

4. Наведіть приклади термінів, які мають різні поняття.

5. Які ознаки входять у зміст понять:

прилеглі кути,

правильний многогранник?

6. Обсяг якого з двох понять більший? (порівняйте перелічені нижче поняття використовуючи символи «<», «>» або «=»)

а) рівнобедрений трикутник  правильний трикутник;

б) неперервна функція  монотонна функція;

в) правильний тетраедр  правильний многогранник;

г) рівносторонній трикутник  правильний трикутник;

д) сектор  сегмент;

е) прямокутник  рівнокутний неправильний чотирикутник.

7. Упорядкуйте поняття так, щоб кожне попереднє поняття було родовим відносно наступного (за допомогою чисел):

а)  ромб,  випуклий чотирикутник,  випуклий многокутник,  паралелограм,  квадрат;

б)  призма, куб,  многогранник,  паралелепіпед,  чотирикутна призма,  правильний паралелепіпед,  прямокутний паралелепіпед;

в)  правильний трикутник,  многокутник,  рівнобедренний трикутник,  трикутник.

8. Представте схематично у вигляді схеми-діаграми Ейлера-Венна співвідношення між обсягами наступних понять:

а) невід’ємне число, недодатне число;

б) гострий кут, тупий кут.

а)

б)

в) раціональне число, ірраціональне число;

г) трапеція, арифметична прогресія;

в)

г)

д)ромб, випуклий чотирикутник, прямокутник, трапеція, випуклий многокутник, паралелограм, квадрат;

є) паралелограм, трапеція, прямокутник, чотирикутник, ромб, квадрат.

д)

є)

ж) многокутник, трикутник, прямокутний трикутник, рівнобедрений трикутник, рівносторонній трикутник, комплексні числа.

Дата добавления: 2015-05-09