Как рассчитать выборку для исследования.

После того, как определен метод исследования и разработан инструмент, определяются параметры исследования: тип, состав и свойства выборки и её объем. Для определения типа выборки надо воспользоваться таблицами в лекциях: определить объем и свойства генеральной совокупности, затем выбрать модель выборки..

Далее, исходя из модели, надо определить математический вид выборки. Для этого надо воспользоваться вот такой схемой:

Математические типы выборок

Если выбрана модель, предусматривающая простую сплошную выборку, то надо воспользоваться следующей схемой:

Случайные сплошные выборки

Таблица объемов выборок позволяет определить объем выборок, исходя из заранее заданного показателя надежности P и заранее заданной допустимой величины ошибки е. Р показывает, какую часть генеральной совокупности максимально сможет охватить выборка (это показывает её надежность), а ошибка показывает, какие минимальные расхождения будут допущены между свойствами генеральной совокупности и свойствами выборки.

Таблица объемов выборок
е P	0,10	0,09	0,03	0,07	0,06	0,05	0,04	0,03	0,02	0,01
0,75
0,80
0,85
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,965
0,970
0,975
0,980
0,985
0,990
0,991
0,992
0,993
0,994
0,995
0,996
0,997
0,998
0,999

Допустим, мы хотим охватить генеральную совокупность с надежностью не менее 80% и допускаем ошибку нашего исследования не менее 10%. При этом мы ничего не знаем о том, какие значения может принимать исследуемая нами переменная, то есть не имеем никакой априорной информации о генеральной совокупности: ни среднего не знаем, ни возможной дисперсии - ничего. Тогда мы просто ищем соответствующее пересечение в таблице (Р=0,80, е=0,10): объем выборки составит 41 человек. Таблица составлена из расчета максимального значения дисперсии дихотомической переменной. Видно, что с увеличением точности выборки её объем быстро растет – если в описанном случае мы увидели объем в 41 человек, то для параметров в Р=95% и е=5% (стандартных для большинства исследований) объем составит уже 384 человека. Поэтому таблицей надо пользоваться в случаях, когда генеральная совокупность относительно небольшая и допустимы значительные величины ошибок.

Чтобы обеспечить небольшой объем выборки для относительно большой генеральной совокупности, надо заранее знать параметры распределения изучаемой переменной: среднее значение и дисперсию. При этом можно воспользоваться приведенной ниже номограммой для расчета выборок (номограмма построена для надежности Р=95%, что вполне достаточно). Для использования номограммы надо знать две величины: коэффициент изменчивости v и допустимую величину ошибки е. Коэффициент изменчивости определяется как коэффициент вариации

то есть для его определения надо знать среднее арифметическое и среднее квадратичное отклонение исследуемой переменной.

Для упрощения расчета коэффициента изменчивости надо знать размах вариации, то есть максимальное и минимальное значение, которых может достигать исследуемая переменная. В этом случае расчет v ведется так:

,где X_max, X_min – максимальное и минимальное значения исследуемой переменной, А - постоянное действительное положительное число (обычно выбирается между 5 и 6).

Номограмма для расчета объема выборки по заданной мере изменчивости и величине ошибки

Пример 1. Предположим, нам известно, что коэффициент изменчивости исследуемой переменной равен 6%. Найдем объем выборки при допустимой ошибке в 5%. Для этого на левой шкале номограммы, обозначенной v%, ищем точку 6. На правой шкале номограммы, обозначенной ε%, ищем выбранное значение ошибки, составляющее 5%. Отмечаем эти точки на линиях и соединяем их по линейке прямой линией. Смотрим, где эта прямая пересекает центральную шкалу, обозначенную n₁. Это пересечение совершается в точке 6. Следовательно, объем выборки составит 6 человек.

Пример 2. Пусть нам известно, что коэффициент изменчивости исследуемой переменной равен 16%. Найдем объем выборки для заданной ошибки в 5%. 16% больше 10%, максимально отмеченных на шкале v%, а шкалы логарифмические, поэтому 16 делим на 10 и на шкале v% номограммы ищем точку 1,6. На правой шкале номограммы ε% ищем выбранное значение ошибки, составляющее 5%. Отмечаем эти точки на шкалах и соединяем их по линейке прямой линией. Смотрим, где прямая пересекает центральную шкалу n₁. Пересечение совершается в точке 0,4. Поскольку мы уменьшили 16% до 1,6%, то есть в 10 раз, то умножаем 0,4 на 100. Объем выборки составит 40 человек (сравните с указанной выше выборкой в 384 человека для Р=95% и е=5% без учета конкретного значения дисперсии).

Пример 3. Исследуется потребление студентами сигарет, причем изучаются только те, кто курит сигареты (генеральная совокупность - курящие). Допустимая ошибка составляет 5%. Заранее известно (например, данные взяты из источников вторичной маркетинговой информации), что студенты выкуривают сигареты в количестве от одной пачки сигарет в три дня до двух пачек в день, причем в среднем курящему студенту хватает одной пачки сигарет на день. Тогда соответствующие значения будут составлять X_max =2, X_min =0,33, а среднее составит 1. Коэффициент изменчивости v составит

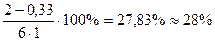
и на левой шкале мы откладываем 2,8%, на правой 5%, соединим их и по центральной шкале номограммы получим отметку 1,2 - это значит, что объем выборки должен быть 120 человек.

Пример 4. Предположим, что при использовании предыдущего примера доступ к целевой репрезентативной группе (курящим) отсутствует. Это значит, что надо включать в выборку как курящих, так и некурящих. В таком случае параметры для расчета будут X_max =2, X_min =0. Какова будет средняя? Расчет средней по выражению (2+0)/2=1 не является правильным, поскольку прежняя средняя рассчитывалась только для курящих, а сейчас не учтено соотношение размеров групп курящих и некурящих. Например, если доля некурящих составляет 60%, а доля курящих - 40%, то тогда средняя составит 0,4.

Сравним возможные размеры выборок и ошибки исследования:

Коэффициент изменчивости 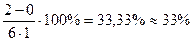Объем выборки по номограмме при допустимой ошибке 5% - 170 человек Рассчитанная по результатам реального исследования ошибка составляет 7%

Коэффициент изменчивости 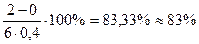Объем выборки по номограмме при допустимой ошибке 5% - 1200 человек Рассчитанная по результатам реального исследования ошибка составляет 2%

Если отсутствуют данные о соотношении репрезентативной и нерепрезентативной групп в генеральной совокупности, то расчет коэффициента изменчивости осуществляется через изменение величины А. Как правило, если средняя рассчитывается по выражению (X_max + X_min)/2, то А уменьшается до 5 и менее.

Как видим, простая случайная выборка для достижения требуемой точности требует значительных объемов. Общий объем выборки можно существенно уменьшить двумя способами:

1) выполняя районирование или стратификацию, то есть выделяя качественно различные группы в генеральной совокупности и размещая выборку именно среди представителей этих групп;

2) выполняя выделение гнезд, то есть разделяя генеральную совокупность на большое количество одинаковых частей и распределяя выборку между этими частями.

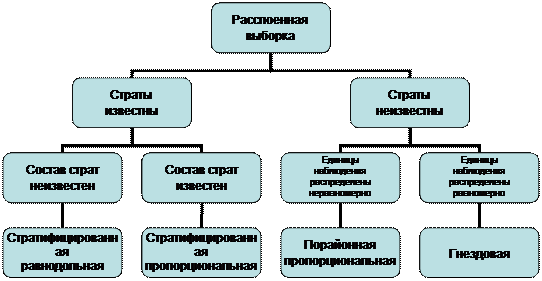
При проведении стратифицированной выборки можно поступать следующим образом (см. схему далее).

Первоначально определяется, какой объем априорной информации известен о генеральной совокупности. Для правильно выполненной стратифицированной выборки минимального объема необходимо знать общую численность генеральной совокупности N, число изучаемых страт i, численность каждой страты N_i, а внутри каждой страты соответствующее среднее значение изучаемой переменной и её дисперсию. Если все эти параметры известны, то с помощью рассмотренной выше номограммы можно рассчитать объем стратифицированной пропорциональной выборки.

Расслоенные выборки

Для этого определяют сначала генеральную дисперсию изучаемой переменной как сумму внутригрупповой и межгрупповой дисперсий, потом определяют генеральное среднее по средним страт, потом определяют коэффициент изменчивости и по номограмме определяют при задании допустимой ошибки общую величину выборки. σ

Генеральная дисперсия равна

где σ²_р - внутригрупповая дисперсия, а σ²_m - межгрупповая дисперсия.

Внутригрупповую дисперсию определяют по известным дисперсиям изучаемой переменной внутри каждой страты

,

где N_i - численность i -той страты, σ²_i - дисперсия i -той страты.

Межгрупповую дисперсию определяют, исходя из известных средних по каждой страте и рассчитанной на их основе генеральной средней:

Далее рассчитывают коэффициент изменчивости изучаемой переменной с помощью генеральной дисперсии и генеральной средней:

Далее по номограмме находят общую численность выборки n. Потом полученное значение распределяют по стратам пропорционально долям их численности в генеральной совокупности:

Если известно число страт, но неизвестен их объем (и/или объем генеральной совокупности), то рассчитывается сначала общий объем выборки указанным способом, а потом он делится на число страт так, чтобы в каждой страте разместилась бы одинаковая доля выборки - это будет стратифицированная равная выборка.

Если неизвестны дисперсии внутри страт, то необходимо знать размах вариации внутри каждой страты, то есть значения X_max и X_min. Тогда дисперсии страт можно рассчитать, исходя из выражения

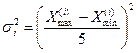
Если неизвестна численность страт, то внутригрупповвая дисперсия рассчитывается как простое среднее арифметическое из дисперсий страт.

Если неизвестны средние в каждой страте, но известен размах вариации, то средние внутри страт определяются как средние между крайними значениями изучаемой переменной

Если наличие страт неизвестно, но по генеральной совокупности известны параметры среднего, дисперсии и плотности распределения единиц наблюдения, то осуществляется районная выборка по гнездовому или пропорциональному способам. Если единицы наблюдения размещены по территории, где находится генеральная совокупность, относительно равномерно (коэффициент вариации плотности размещения составляет не более 15-25%), то используется выделение гнезд, каждое из которых вмещает в себя одинаковое число единиц наблюдения. Гнезда выделяются так, что имеют одинаковый размер (например, площадь). Число гнезд определяется пропорционально отношению общего размера выборки n к общему числу единиц наблюдения N. Из каждого гнезда отбирается только одна единица наблюдения, размещение выборки по гнездам осуществляется равномерно-механическим или случайным методом.

Если размещение единиц наблюдения по изучаемой территории неравномерно, то она разделяется на районы с одинаковым числом единиц наблюдения в каждом - это порайонная пропорциональная выборка. Для этого рассчитывается общий объем выборки по номограмме, после чего эта выборка распределяется по районам пропорционально численности единиц наблюдения. Внутри районов в этом случае размещение выборки выполняется либо гнездовым, либо иным способом, аналогично известным процедурам размещения выборок.

Пример 5. Воспользуемся примером 3, изучающим потребление сигарет. Если нет никаких данных о возможных параметрах изучаемой переменной, то при данных Р=95%, е=5% объем выборки составит 384 человека. Выделим две страты - мужчин и женщин. Пусть априори известно (например, из проведения пилотного исследования), что потребление сигарет в пачках за день составляет у мужчин X_max =2, X_min =0,33, у женщин X_max =3, X_min =0,1. Вычислим объем выборки в этом случае

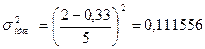
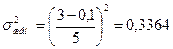
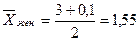
Поскольку о соотношении численностей страт нам ничего не известно, то принимаем, что их численности равны и доли их численностей в генеральной совокупности составляют по 0,5. Тогда внутригрупповая дисперсия будет

а межгрупповая

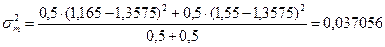
при генеральном среднем

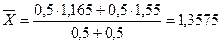
Тогда генеральная дисперсия будет

и коэффициент изменчивости составит

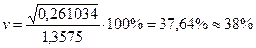
По номограмме при допустимой ошибке 5% объем выборки составит приблизительно 240 человек (более чем на 140 меньше, чем по таблице). В данном случае эта выборка должна быть разделена на 120 мужчин и 120 женщин.

Если и этот объем выборки слишком велик, то нужно увеличивать количество страт, добиваясь того, чтобы размах вариации в каждой страте был минимален, а размеры страт близки, то есть стремиться к минимуму суммарной дисперсии.

В случае, когда известен размер генеральной совокупности в целом, то возможно корректировать размер выборки на бесповторность следующим образом:

1) для известных v% и e рассчитывается по номограмме размер выборки n₁;

2) заданная допустимая ошибка корректируется с учетом размера генеральной совокупности

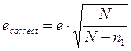
3) по номограмме для скорректированной ошибки e_correct и v% находится новый объем выборки n₂.

Пример 6. Предположим, что исследование проводится для целевого сегмента объемом 1600 единиц наблюдения при v% =25% и e =5%. По номограмме объем выборки тогда составит 100 единиц наблюдения. Корректируем ошибку с учетом размера выборки

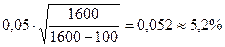
По номограмме скорректированный объем выборки составит (при v% =25% и e =5,2%) 90 единиц наблюдения.

ГЛАВА 1.

В этой части работы студент обрабатывает собранные им данные и делает вывод относительно поставленной задачи: как решить поставленную проблему.

Для обработки студент может использовать MS Excel, SPSS, Statistika for Windows, MatLab, MatCad и другие программы обработки больших массивов данных. Основные задачи, решаемые при использовании этих средств:

верификация данных:

установление законов распределения;

установление взаимосвязей между данными;

классификация и сегментация данных;

прогнозирование развития событий.

Последовательность обработки данных исследования

1. расчет в рамках анализа двумерных распределений по каждой таблице данных, коэффициента вариации, корреляционного отношения и стандартных отклонений4
2. расчет корреляционной и ковариационной матриц;
3. выбор массива данных по заранее заданным условиям;
4. вычисление распределений (при учете заданных условий);
5. перекодировка (исправление ошибок в данных);
6. введение новых показателей (расчет индексов).

Ниже в таблице описаны возможные методы анализа данных. Не следует, разумеется, применять их сразу все. Студент выбирает именно те 1-2 метода, которые наиболее подходят для раскрытия поставленной проблемы.

Количественные методы анализа данных маркетинговых исследований

1.Методы сжатия описательной статистики

2.Методы анализа систем показателей

1.1 Группирование

1.2 Оценка параметров распределения

1.3 Ковариационная и корреляционная матрица

2.1 Ориентация на интегральную качественную характеристику

2.2 Ориентация на количественный признак

2.2.1 Дисперсионный анализ

2.2.2 Корреляционно-регрессионный анализ

2.2.3 Причинный анализ

2.1.1 Без априорной информации об исследуемом признаке

2.1.2 С априорной информацией о классах признака

2.1.3 С априорной информацией о возрастании (убывании) признака)

2.1.1.1 Методы экспертных оценок

2.1.1.2 Анализ матрицы данных.

2.1.3.1 Усиление шкалы по результирующему признаку

2.1.3.2 Оценка существенности показателя (ранговые корреляции)

2.1.1.2.1Факторный анализ

2.1.1.2.2Латентно-структурный анализ

2.1.1.2.3Кластерный анализ

2.1.1.2.4 Методы оценки значимости показателя

2.1.2.1 Методы усиления номинальной шкалы по результирующему признаку

2.1.2.2 Оценка существенности показателей системы

2.1.2.2.1 Методы теории распознавания образов

2.1.2.2.2 Методы теории информации

2.1.2.2.3 Методы теории графов

Для определения основных характеристик в зависимости от применявшихся вопросов могут быть применены слудующие методы анализа измерений по шкалам в вопросах:

Тип шкалы	Типы статистик
Номинальная	Частоты f, мода Mo, коэффициент сопряженности Кт Чупрова, коэффициенты Q, F, s Пирсона
Порядковая	Медиана Me, квантили Q1, Q2, Q3, коэффициенты ранговой корреляции Спирмена и Кэндалла
Интервальная и относительная	Выборочная средняя x^~ и генеральная средняя x^-, средние доли, полная и межгрупповая дисперсии, коэффициент корреляции r, коэффициент s Пирсона

Статистические методы выявления связей

Шкала результирующего (итогового) признака	Шкала факторного признака (предиктора)	Метод статистической обработки
Количественные (И,О,А,Р)	Количественные (И,О,А,Р)	Регрессии Корреляции
Количественные (И,О,А,Р)	Время (И)	Динамика временных рядов
Количественные (И,О,А,Р)	Неколичественные (К,П)	Дисперсионный анализ
Количественные (И,О,А,Р)	Количественные и неколичественные	Ковариационный анализ Типологическая регрессия
Неколичественные (К)	Количественные (И,О,А,Р)	Дискриминантный анализ Кластерный анализ Таксономия Расщепление смесей
Неколичественные (П)	Неколичественные (К,П)	Ранговые корреляции Анализ таблиц сопряженности
Количественные и неколичественные	Количественные и неколичественные	Логические решающие функции
Типы шкал в вопросах: И - интервальная, О - относительная, А- абсолютная, Р - разностная, П - порядковая, К - классификационная (номинальная)

Например, корреляционный анализ для сегментации потребителей выполняется так:

1. выделяются средние значения, стандартные отклонения, коэффициент вариации, ошибку среднего значения и доверительный интервал;
2. рассчитывается ковариационная и корреляционная матрица (например, в MS Excel);
3. вычисляется «близость» объектов в пространстве характеристик (для сегментации);
4. вычисляются пути максимальной корреляции в целях группировки переменных;
5. вычисляются пути максимального расстояния по матрице расстояний в целях классификации объектов;
6. определяются наиболее близкие группы, которые и будут сегментами потребителей;
7. проверяется мера близости групп (например, корреляционное отношение).

В конце этой главы студент описывает результаты анализа данных, так чтобы были ясны его решения поставленных задач работы, окончатеьные выводы и их формулировки.

Заключение

В этом разделе студент формулирует полное решение проблемы, поставленной в начале своей работы.

Список литературы

Список использованных источников (список литературы) надлежит выполнять в конце текста работы сообразно ГОСТ 7.1-84, например:

Зиннуров У. Г. Основы маркетинговых исследований: Учебное пособие / У. Г. Зиннуров; Уфимск. гос. авиац. техн. ун-т. Уфа, 1996.- 110 с.

Источники в списке располагаются в алфавитном порядке. На все перечисленные источники в работе необходимо сделать ссылки. Постраничные сноски не допускаются.

В случае, если источником являются сайты Интернета, необходимо указывать полностью адрес того сайта (копируя его адресную строку), на котором была получена конкретная информация. При этом приводится дата последнего обращения к этому сайту, например:

http://www.brukhoffbossmag.ru/Articles/Lopoukhov/article1.html (20.10.2005)

На сайты также необходимо делать ссылки в тексте курсовой работы.

Дата добавления: 2015-05-09