Первый способ настройки УЛМ

Первым способом настройки, используемым в УЛМ. является фиксация некоторых входов. Для этого способа справедливо следующее соотношение между числом аргументов и числом настроечных входов. Пусть число аргументов n и требуется настройка на любую из функций. Тогда число комбинаций для кода настройки, равное числу функций, есть 2^{2^n}. Для двоичного кода число комбинаций связано с разрядностью кода выражением 2^m, где m - разрядность кода. Приравнивая число воспроизводимых функций к числу комбинаций кода настройки, имеем для числа настроечных входов соотношение m = 2ⁿ.

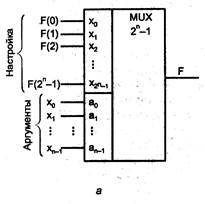Рис. 2.2 Схема использования мультиплек­сора в качестве УЛМ (а), примеры воспроиз­ведения функций при настройке константами (б) и при переносе одного аргумента в число сигналов настройки (в)

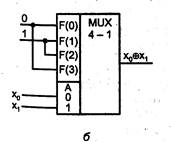
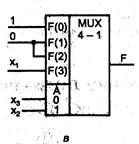
Рис 2.2

Полученному выражению отвечает соотношение между числом входов разного типа для мультиплексора. При этом на адресные входы следует подавать аргументы функции, а на информационные входы — сигналы настрой­ки (рис. 2.2, а). Таким образом, для использования мультиплексора в качест­ве УЛМ следует изменить назначение его входов.

Рис. 2.2, а — иллюстрируетвозможность воспроизведения с помощью мультиплексора любой функции n аргументов. Действительно, каждому на­бору аргументов соответствует передача на выход одного из сигналов на­стройки. Если этот сигнал есть значение функции на данном наборе аргу­ментов, то задача решена. Разным функциям будут соответствовать разные коды настройки. Алфавитом настройки будет {0,1} — настройка осуществля­ется константами 0 и 1. На рис. 2.2, б показан пример воспроизведения функции неравнозначности Х1+ Х2 с помощью мультиплексора "4—1".

Большое число настроечных входов затрудняет реализацию УЛМ. Для УЛМ, расположенных внутри кристалла, можно вводить код настройки последова­тельно в сдвигающий регистр, к разрядам которого подключены входы на­стройки. Тогда внешним входом настройки будет всего один, но настройка будет занимать не один такт, а 2ⁿ тактов. Возможны и промежуточные по­следовательно-параллельные варианты ввода кода настройки.

Дата добавления: 2015-05-09