Оценивание неизвестных параметров модели 1 страница

В этом параграфе будет рассмотрена задача построения точечных оценок параметров 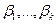и 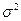модели линейной регрессии (5.1) —(5.2).

1. Метод наименьших квадратов. Общим методом оценивания неизвестных коэффициентов регрессии 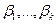является раз­работанный К. Гауссом (1809 г.) и А. Марковым (1900 г.) метод наименьших квадратов, в соответствии с которым оценки этих параметров находят из условия обращения в минимум квадратичной формы

, (5.4)

представляющей собой сумму квадратов разностей между наблюдениями и их математическими ожиданиями. Точку 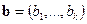, удовлетворяющую равенству 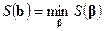, называют, по определению, оценкой наименьших квадратов (о. н. к.) параметра .

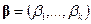Пусть 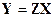; тогда с помощью непосредственных вычислений можно убедиться, что система уравнений 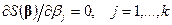, в матричной форме записывается в виде

,

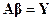где матрица 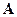задана в (5.3). Это уравнение для экстремальных точек 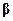называют нормальным уравнением метода наименьших квадратов. Справедливо следующее утверждение.

Теорема 5.1. Пусть 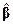— любое решение нормального урав­нения. Тогда

и, следовательно, этот минимум одинаков для всех .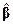

Если 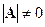, то о. н. к. единственна и определяется равенством

. (5.6)

□ Пусть — произвольное фиксированное значение 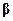; тогда из (5.4) имеем

,

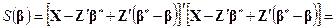
Если 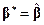, то

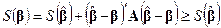
поскольку матрица 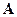неотрицательно определена. Таким образом, минимум 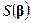равен 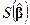, достигается при 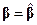и одинаков для всех решений 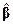уравнения (5.5). Отсюда следует, что любое решение нормального уравнения является о. н. к. для 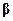. Для невырожденной матрицы 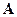уравнение (5.5) однозначно разрешимо и, следователь­но, в этом случае о. н. к. единственна и имеет вид (5.6). ■

В ряде случаев интерес представляют не сами параметры 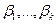, а их некоторые линейные комбинации, т. е. новый параметрический вектор 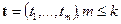, связанный с 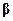соот­ношением , где 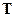— заданная матрица размером 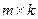. В этом случае о. н. к. 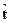для 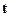определяется равенством , где 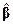— любое решение нормального уравнения (5.5). Если 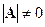, то из (5,6) следует, что 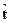определяется однозначно и имеет вид

. (5.9)

2. Оптимальность оценок наименьших квадратов. Исследуем свойства полученных оценок. В общем случае будем рассматри­вать задачу оценивания вектора в классе линейных оценок, т.е. оценок вида 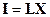, являющихся линейными функциями от наблюдений .

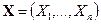Теорема 5.2. Пусть матрица 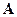не вырождена. Тогда для произвольного вектора о. к. к. 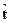, определенная равенством (5.9), является несмещенной оценкой с минимальной дисперсией в классе всех линейных несмещенных оценок 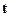; при этом матрица вторых моментов случайного вектора 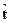имеет вид

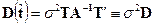. (5.10)

□ Из (5.9) и (5.1) имеем

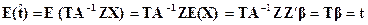
т.е. 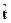- линейная несмещенная оценка 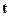. Пусть 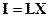— произвольная линейная несмещенная оценка 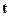, т. е. 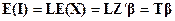. Это равенство должно выполняться для всех 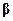, поэтому отсюда следует, что

. (5.11)

Из (5.2) находим

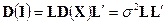. (5.12)

Наша цель — минимизировать дисперсии оценок 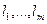, т.е. диагональные элементы матрицы 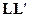. Для этого запишем тождество

которое непосредственно следует из равенства (5.11). Каждое слагаемое правой части этого тождества имеет вид 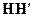, откуда следует неотрицательность диагональных элементов. Но от 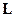зависит только второе слагаемое, поэтому диагональные элементы 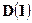одновременно достигают минимума тогда и только тогда, когда 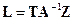. Соответствующая оптимальная оценка имеет вид 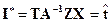. т. е. совпадает с о. н. к. (5.9). Наконец, формула (5.10) следует из соотношения (5.12), если подставить вместо 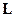найденное оптимальное решение. ■

В качестве простого следствия теоремы 5.2 получаем, что 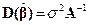или

(5.13)

где

Замечание. Если матрица 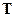имеет вид 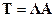, то формулы (5.9) и (5.10) принимают соответственно вид

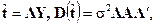
т. е. необходимость в вычислении обратной матрицы 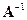для нахождения о. н. к. и их вторых моментов отпадает.

Итак, теорема 5.2 позволяет решить задачу о построении оптимальных оценок для произвольных линейных функций от коэффициентов регрессии; это оценки наименьших квадратов.

3. Оценивание остаточной дисперсии. Из равенства (5.4) имеем;

.

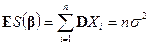Далее, учитывая (5.13), найдем

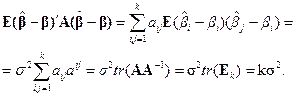
Отсюда и из тождества (5.8) следует, что , т.е. несмещенной оценкой для остаточной дисперсии является статистика

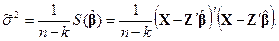(5.14)

Вектор 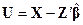называют остаточным вектором, а его компоненты — остатками. Таким образом, оценка равна сумме квадратов остатков, поделенной на (разность между числом наблюдений и числом параметров ).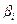

Приведем другое выражение для (5.14), которое понадобится в дальнейшем. Используя представление (5.6), запишем остаточный вектор в виде

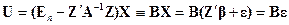. (5.15)

Непосредственно можно проверить, что матрица 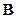, определяемая этим равенством, симметрична и идемпотентна 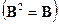; следовательно, вместо (5.14) можно использовать представление

(5.16)

показывающее явную зависимость оценки от наблюдений. Наконец, из (5.15) имеем, что первые и вторые моменты остаточного вектора имеют вид

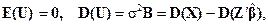а (5.17)

4. Обобщенные о. н. к. Ранее рассматривался случай, когда на возможные значения параметров не накладывалось никаких ограничений, т. е. областью их возможных значений было все евклидово пространство 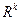. Однако в ряде задач допустимые значения 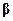бывают ограничены теми или иными условиями. Часто эти условия имеют вид линейных ограничений на параметры 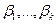, что в общем виде будем записывать так:

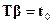, (5.18)

где 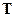-некоторая заданная матрица размером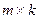 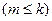и - заданный -мерный вектор такой, что система (5.18) совместна. Другими словами, условие (5.18) означает, что

допустимые значения коэффициентов регрессии 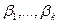удовлетворяют заданным линейным ограничениям

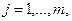, (5.19)

где 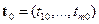и 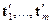- строки матрицы 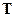. Естественно предполагать, что ограничения (5.19) линейно независимы (иначе можно перейти к меньшему числу уравнений, исключив линейно зависимые). Таким образом, в дальнейшем будем считать,, что 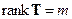(случай 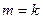, однозначно фиксирующий вектор 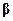, в последующих рассуждениях формально допускается).

Рассмотрим задачу оценивания параметров 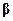в этой усложненной ситуации. Обозначим

(5.20)

и назовем обобщенной оценкой наименьших квадратов то значение 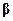(удовлетворяющее условию (5.18)), при котором 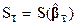. Нахождение обобщенной о. н. к. - это задача нахождения условного экстремума функции 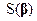, и ее можно решить методом неопределенных множителей Лагранжа. Приведем только окончательный результат:

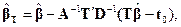(5.21)

где 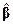- обычная о. н. к. (без ограничений на параметры 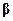), определенная равенством (5.6), а матрица размером 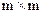положительно определена.

Докажем тот факт, что - точка условного минимума квадратичной формы . Из (5.21) непосредственно получаем, что , т.е. точка , удовлетворяет условию (5.18). Воспользуемся далее разложением (5.7) для 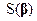и положим в нем :

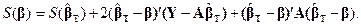
Так как , то из (5.21) следует, что .

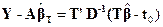Учитывая также, что 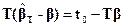, получаем равенство

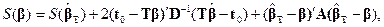(5.22)

справедливое при всех 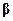. Пусть теперь 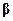удовлетворяет условию (5.18); тогда средний член обращается в нуль и

причем равенство достигается только при .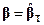

Замечание. Полагая в (5.22) 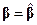. и учитывая, что в силу (5.21) 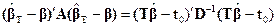, получаем следующее представление условного минимума 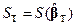через абсолютный минимум :

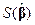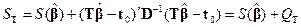(5.23)

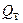( определено этим равенством).

5. Оптимальный выбор матрицы плана. Рассмотрим «активный» эксперимент, т. е. когда значения факторов для каждого опыта выбирает исследователь. Покажем, как в этом случае оптимально задать матрицу плана 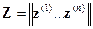, где 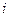-й столбец 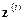- комбинация значений факторов для 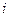-го опыта 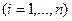. В качестве критерия оптимальности естественно использовать величину дисперсий оценок 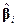[см. (5.13)]; тогда задача сводится к выбору такой матрицы 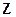, чтобы диагональные элементы матрицы 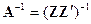были минимальны.

Если значения факторов выбирать произвольными, то все моменты матрицы 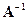можно сделать одновременно как угодно малыми, так как если 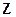заменить на 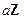. то 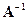заменится на 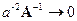при 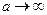. Чтобы исключить этот случай, предположим, что значения факторов можно менять в ограниченных областях, именно: наложим ограничения вида

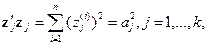(5.24)

где 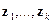—столбцы матрицы 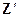(наборы значений 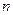уровней соответствующих факторов) и —заданные положительные константы.

При ограничениях (5.24) на допустимые значения 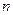уровней каждого фактора следует подобрать комбинацию значений факторов (т. е. выбрать столбцы матрицы 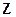) так, чтобы дисперсии о. н. к. параметров 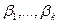приняли наименьшие возможные значения.

Теорема 5.3. При условиях (5.24) имеют место неравенства

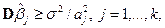
и минимум достигается тогда и только тогда, когда столбцы матрицы ортогональны.

 Пусть 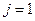. Запишем матрицу 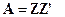в виде

где 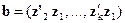Тогда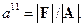

Далее, умножая определитель 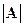справа на определитель, равный 1, получаем следующую формулу:

Отсюда, учитывая соотношения (5.13) и (5.24), имеем

так как 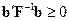. Знак равенства имеет место только при (поскольку подматрица положительно определена), т.е. при (первый столбец матрицы 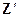ортогонален всем остальным столбцам). Доказательство для других можно получить простой перенумерацией факторов. ■

В заключение отметим, что для оптимальной матрицы плана 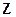матрица 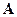является диагональной с диагональными элементами 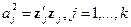, поэтому проблема обращения 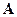для вычисления о. н. к. и их вторых моментов отпадает, в этом случае

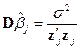, . (5.25)

6. Примеры применения метода наименьших квадратов.

Пример 5.1 (простая регрессия, оценивание параметров). Проиллюстрируем общую теорию на примере важного для практических приложений случая простой регрессии, когда число параметров т.е. а векторы 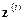имеют вид 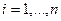. Тогда

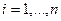, (5.26)

т. е. среднее значение наблюдений является линейной функцией одного фактора 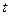. Так, 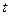может быть температурой, при которой производится эксперимент, дозой лечебного препарата, возрастом обследуемых лиц и т. д., и речь идет об изучении связи между откликом (исходом эксперимента) и фактором 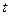на основании выборки, при этом регистрируют 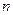пар измерений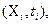 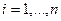, где 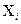наблюдается при значении 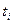фактора .

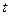Прямую соответствующую (5.26), называют линией регрессии, а коэффициент 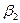- ее наклоном.

В данном случае матрицы 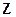, 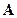и столбец 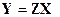равны:

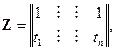
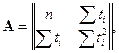
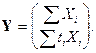
Будем предполагать, что не все 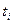одинаковы (чтобы 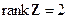), тогда

(черта сверху означает арифметическое среднее) и

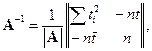
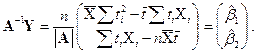
В результате несложных преобразований запишем оценк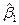и и 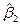в следующем удобном для вычислений виде:

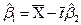. (5.27)

Вторые моменты этих оценок образуют матрицу 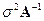, поэтому

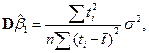
Наконец, величина 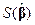(5.14) равна

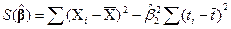(5.28)

и несмещенная оценка для остаточной дисперсии 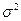имеет вид

.

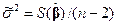Пример 5.2 (параболическая регрессия). Пусть -й фактор , является полиномом степени 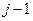от общей переменной 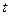; тогда 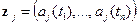, 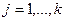- набор его значений для 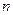уровней, a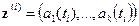 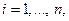- комбинация значений факторов для 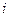-гo опыта. Таким образом, матрица плана определяется выбором 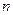точек 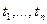значений общего фактора 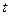для 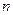опытов. В этом случае среднее значение 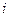-го наблюдения 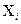имеет вид

Дата добавления: 2015-05-09